２０１２年　数楽工作倶楽部　第３回製作物

第１回・第２回で製作した「菱形三十面体」と「菱形六十面体」、これに「菱形二十面体」を加え、５回回転対称の空間充填モデルを製作しました。これは、「準結晶」とよばれる２０１１年ノーベル化学賞受賞理由ともなった原子構造で、並行移動による周期性を持つ通常の結晶とは異なる、回転対称の規則性を持っています。
数学の世界では、二種類の菱形で実現される非周期的なタイリングであるペンローズタイルや、非周期的な空間充填の問題、また半正多面体の幾何学構造とも深い関係があります。

今回用いる３種類の多面体です。


茶色： 菱形六十面体、紫： 菱形三十面体、黄色： 菱形二十面体（菱形三十面体を薄っぺらく円盤状にした立体で、６本の帯で編む菱形三十面体に対して、１本少ない５本の帯で編む）以下、単に６０面体、３０面体、２０面体と呼ぶことにします。
使用する個数は、６０面体×１３、３０面体×２０、２０面体×１２です。
（菱形２０面体のパーツＤＬ）
※菱形２０面体は５本の帯で作られます。作り方は、菱形３０面体を編む行程から６本目の帯の編みこみを省いたものです。

前回までに編み方をマスターした工作倶楽部メンバー総出で作りました↓


組み立ては次の通りです。（クリックで拡大します）

�@６０面体のまわりに３０面体をつなげる。
　　（裏返したもの）

�A６０面体５個を加える。


�B３０面体５個を加える。


�C内部のくぼみを、２０面体１２個で囲まれた６０面体で埋める。
　→　　→

　→　

�D３０面体５個を加える。（３６度回転しています）


�E６０面体５個と３０面体５個を加える。


�F６０面体でふたをすると完成。


外側から見える６０面体と３０面体をそれぞれサッカーボールの黒い正五角形と白い正六角形とみなすと、この立体は切頂二十面体とみなすこともできます。

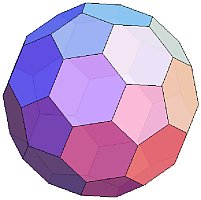（切頂二十面体）



この立体を真上から眺めると、平面への射影がペンローズタイルになることがわかります。

Back