2012年 数楽工作倶楽部 第4回製作物
今回の製作物は、一般の人たちにもよく知られている折り紙で作る多面体(くすだま)です。折り紙で作った「ユニット」を組み合わせて多面体を作ることから「ユニット折り紙」とも呼ばれています。ユニットにも様々な種類があるのですが、ここでは最もポピュラーは「薗部式」というユニットを使用することにします。薗部式のユニットを使った多面体の工作は以前の活動でもやったことがありますが、今回は倶楽部のメンバー総出でもう少し大きなサイズのモデルを作ってみました。
正八面体
合同な正三角形で構成された多面体を作る場合、薗部式ユニットでは一本の辺を一個のユニットに対応させます。たとえば、以前の活動で作った12個のユニットでできる下のモデルは、12本の辺を持つ「正八面体」に対応します。

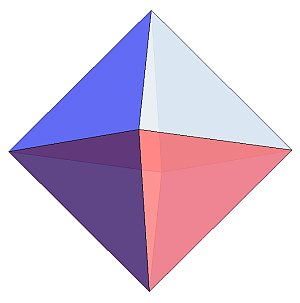
実際、このモデルは8個の下のような「3個のユニットで作られる3枚の直角二等辺三角形からなる三角錐」で構成されていますが、この三角錐の正三角形の底面だけを取り出すと、右上の正八面体とみなすことができます。

三角錐が凹型になるように組んでいった下のモデルを見ると、これらのモデルが正八面体に対応することは明らかです。

正二十面体
30個のユニットでできる下のモデルは、30本の辺を持つ「正二十面体」に対応します。

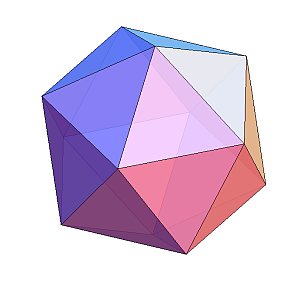
下のように三角錐が凹型になるようにこのモデルを組んでゆくと、まさに正二十面体に対応することがわかります。

このように、それぞれの面を三角錐に対応させることによって、「合同な正三角形だけで構成される多面体」は、辺の数と等しい個数のユニットで構成することができます。一方、下のような「正方形」、「正五角形」、「正六角形」の面を持つ多面体」を作る場合には、少し工夫が必要です。
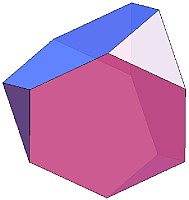
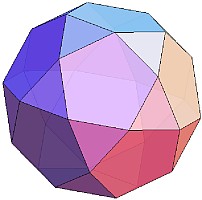
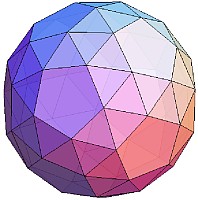
それぞれの面を、4枚、5枚、6枚の正三角形を組み合わせることによって下のようなモデルで表現します。



これによって、辺の長さが等しい正三角形から正六角形までの面で構成される多面体のモデルをユニット折り紙で構成することができます。
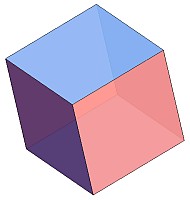
立方体


上のモデルは、立方体とは似ても似つかないように見えますが、前述のルールで構成した紛れもない立方体です。
立方体は6個の正方形で構成されるため、辺の数は
6×4÷2=12(本)
です。
しかし、実際には正方形を「4個の正三角形で作られる四角錐」で表現するので、ここでいう立方体は、本来の立方体の正方形に対応する面がそれぞれ4個の正三角形に置き換わったものです。従って、24(=4×6)個の正三角形で構成される多面体となります。よって、この立体の辺の数(=ユニットの数)は次のようになります。
24×3÷2=36(本・個)
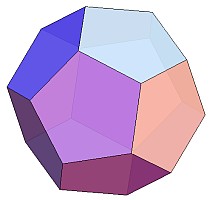
正十二面体

正十二面体は、12個の正五角形で作られるため、辺の数は
12×5÷2=30(本)
です。しかし、実際には正五角形を「5個の正三角形で作られる五角錐」で表現するので、ここで作る正五角形に対応する多面体は、60(=5×12)個の正三角形で構成されています。よって、この立体の辺の数(=ユニットの数)は次のようになります。
60×3÷2=90(本・個)
切頂四面体


切頂四面体は、4個の正三角形と4個の正六角形で作られます。正六角形を「6個の正三角形で作られる六角錐(実際には高さが0となり正六角形と一致する)」で表現するので、ここで作る切頂四面体に対応する多面体は、28(=4+6×4)個の正三角形で構成されています。よって、この立体の辺の数(=ユニットの数)は次のようになります。
28×3÷2=42(本・個)
二十・十二面体

二十・十二面体は、20個の正三角形と12個の正五角形で作られます。よって、正五角形を5個の正三角形で作られる五角錐とした対応する多面体は、80(=20+5×12)個の正三角形で構成されます。よって、この立体の辺の数(=ユニットの数)は次のようになります。
80×3÷2=120(本・個)
捩れ十二面体

捩れ十二面体は、80個の正三角形と12個の正五角形で作られます。よって、上と同様に対応する多面体は、140(=80+5×12)個の正三角形で構成されます。よって、この立体の辺の数(=ユニットの数)は次のようになります。
140×3÷2=210(本・個)
切頂十二面体

切頂十二面体は、12個の正五角形と20個の正六角形で作られます。よって、上と同様に対応する多面体は、180(=5×12+6×20)個の正三角形で構成されます。よって、この立体の辺の数(=ユニットの数)は次のようになります。
180×3÷2=270(本・個)
斜方二十・十二面体

斜方二十・十二面体は、20個の正三角形、30個の正方形、12個の正五角形で作られます。よって、上と同様に対応する多面体は、200(=20+4×30+5×12)個の正三角形で構成されます。よって、この立体の辺の数(=ユニットの数)は次のようになります。
200×3÷2=300(本・個)

今回使用したのは一辺5cmの正方形の折り紙で製作したユニットです。斜方二十・十二面体以外には補強や糊付けは行っていません。
このサイズでは「二十・十二面体」以上のモデルは自重で歪んでしまいます。
ポピュラーな正二十面体(ユニット30個)を作ったことがある方への、次のステップとしてのおすすめは「正十二面体(90個)」か「二十・十二面体(120個)」あたりだと思います。ただし、ユニットの大きさによっては、これらのモデルも自重で歪んでしまうことがあるので、できるだけしっかりとした紙と小さ目のユニットで作ることをお勧めします。
正多面体や半正多面体では、これらの他にも下のような立体(左から右に、「立方八面体」、「切頂八面体」、「斜方立方八面体」、「捩れ立方体」)がユニット折り紙で製作可能です。
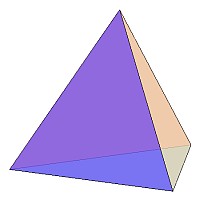
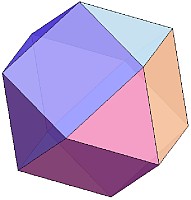
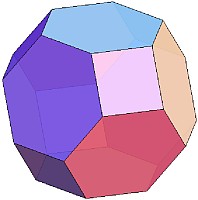
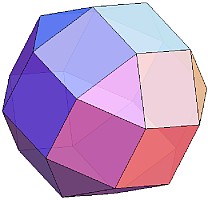
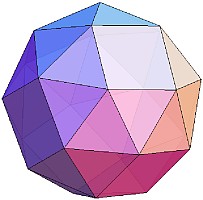
必要なユニットの個数は、それぞれ、6個、48個、108個、84個、84個です。
数楽工作倶楽部でも、近いうちに全立体制覇を行う予定です。
Back





























