
2013年度 数楽工作倶楽部 第1回製作物
円錐で作る正十二面体
今回は、円錐で「正十二面体」を作ってみました。

正多面体は、正多角形を底面に持つ合同な角錐を集めて作ることができます。例えば、正十二面体は、下のような正五角形を底面に持つ5角錐12個で作られると考えられます。
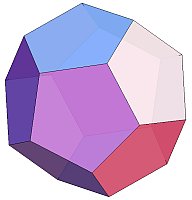 =
= 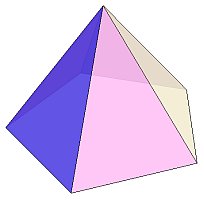 ×12
×12
このようなに「角錐」を組み合わせて「多面体」を作るのは、折り紙のユニットで作るくす玉の定番の製作方法なのですが、今回は少し趣向を変え、5角錐の代わりに下のような5角錐に内接する「円錐」を組み合わせて正十二面体を製作してみることにしました。
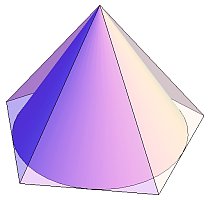
この方法のメリットは、何より部品の製作が容易であることです。実際、円錐の展開図は扇形なので、簡単に大量の部品を製作することができます。この時、唯一考えなければならないのは、扇形の中心角を何度にすればよいか、という問題です。
5角錐の計算
はじめに、一辺の長さが1の正五角形の各部の値について、次のような事実を確認しておきましょう。
(三角関数が出てきていますが、下の「R」や「S」の値は「三平方の定理」だけを使っても求めることができます。)
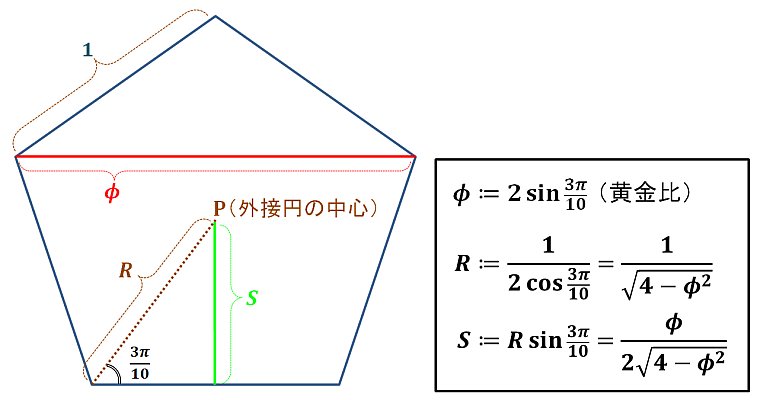
これを用いて、正十二面体を構成する「5角錐の辺の長さの比」を求めてみることにします。
まず、正十二面体から下図のように三角錐を切り出します。
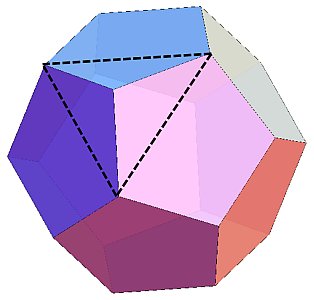 ==>
==> 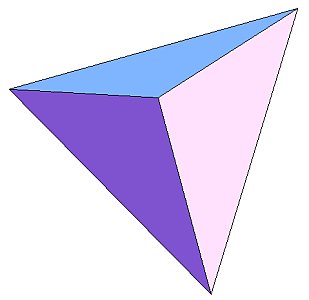
三平方の定理より、この三角錐に関して次の図中の値がわかります。
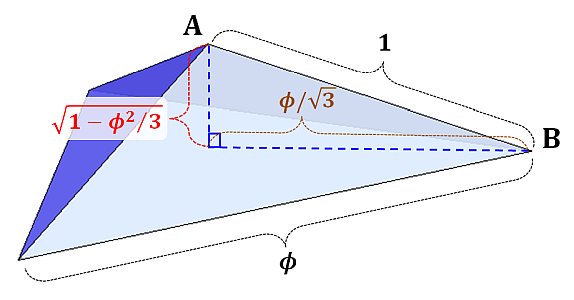
ここで、正十二面体の外接球の半径をr, 中心をOとすると、外接球は正十二面体の頂点A,Bを通るため、次のように r の値を求めることができます。
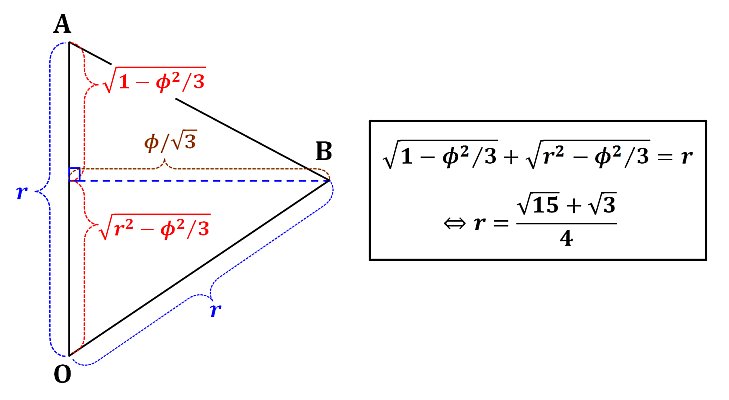
ここで紹介した計算方法は、基本的に「三平方の定理」のみを用いるものでしたが、「ベクトル」を用いるともっとスマートに求めることができます。
円錐の計算
円錐と5角錐の各値は、次のようになることは簡単に計算することができます。
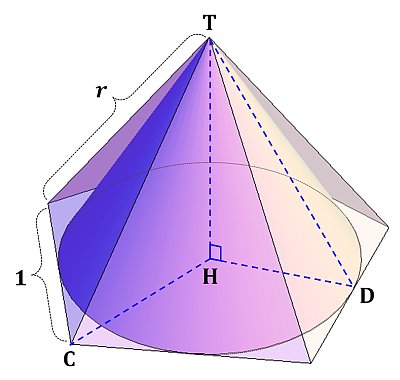
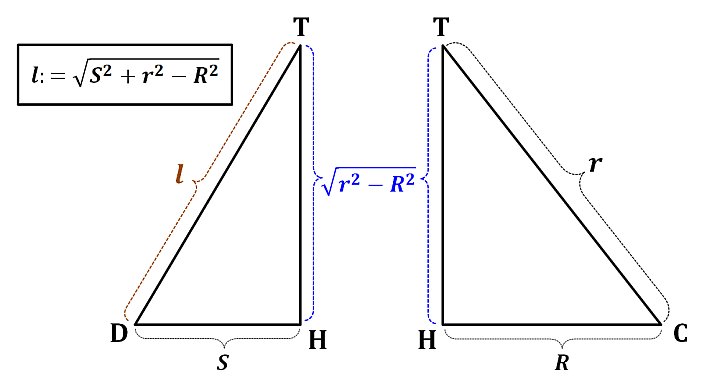
以上より、求める円錐の「底面の円の半径DH」と「稜線の長さDT」の比は次のようになることが分かります。
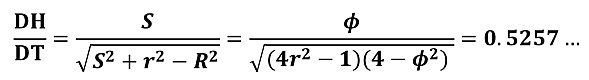
よって、円錐の展開図の扇形の中心核は、360×0.5257...度より、約189度になることがわかります。
モデルの製作 (この型紙を3枚使用します)
製作はいたって簡単なので、詳しい解説はしません。
※上の型紙では「のりしろ」を3枚分(189÷5×3度)とっていますが、1枚分(189÷5度)でも強度的には問題無いと思います。
1.部品の切り抜き: 今回は両面色紙を3色使用し、切り抜きには「円切りカッター」を使いましました。
(下の写真では4色になっていますが・・)

2.円錐の製作: 丸めて「のりしろ」の部分を接着します。スティックのりを使うと紙が歪みません。

3.組み立て: 側面の点線同士がぴったり重なるように組み立ててゆきます。接着剤の量は極力少なめにし、ヘアピンを使うときれいに固定できます。

完成!

次は別の正多面体・半正多面体の製作に挑戦します。