
2013年度 数楽工作倶楽部 第4回製作物
三次元グラフペーパクラフト1
今回作るのは、比較的ポピュラーなネタにもかかわらず、これまで作っていなかった三次元グラフの紙工作です。
コンピューターが用いられる以前は、特に教育現場で、平面上では表すことが困難な三次元空間上のグラフの概形を説明するために、このような模型が用いられていたようです。下の写真は、「ロンドン科学博物館」と「ゲッチンゲン大学」に展示されている模型です。
今回制作したのは、二次曲面の一種である双曲放物面(通称「馬の鞍型」)とよばれる曲面です。
(x,y) 平面の上に波打つ曲面は、一般的には z=f(x,y) と表されますが、特に双曲放物面とよばれる曲面は次のように表されます(x と
y が入れ替わっても構いません)。
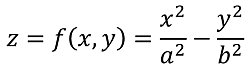
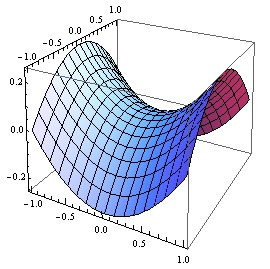
a=b=2
放物双曲面はその名前の通り、z を定数とすると上の方程式を満たす点 (x, y) の集合は双曲線になることがわかります。また、y を定数とすると、方程式を満たす点 (x, z) の集合は下に凸の放物線となり、x を定数とすると、方程式を満たす点 (y, z) の集合は上に凸の放物線になります。従って、 (x, y, z) 空間上にある双曲放物面を、y軸、x軸と直交する平面で切断した場合、その切断面はそれぞれ q, p をパラメータとする次の放物線となります。
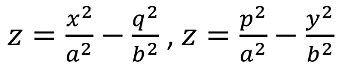
この様子は、下図のように曲面を y 軸方向、 x 軸方向から眺めると良くわかります。
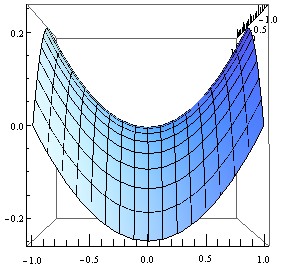
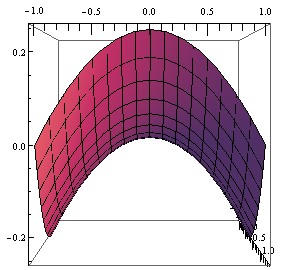
従って、これらの放物線を直交するように組み合わせてゆけば、切断面の集合から目的の曲面を再現することができます。このようにして作ったのが下の模型です。
特に b=a とし、この曲面を z 軸に関して反時計回りにθ回転させると、その曲面を表す関数は次のようになります。
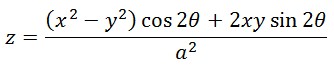
特にθが45度の時には次のようになります。
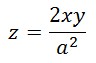
先ほどと同様に、この曲面をy軸、x軸と直交する平面で切断した場合、切断面はそれぞれ q, p をパラメータとする次の一次関数となるため、断面は曲線ではなく直線になります。(すなわち、この曲面は線織面であることがわかります。)
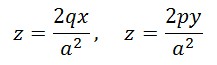
この事実をふまえて作ったのが下の模型です。
二つのモデルの中間となるθ=22.5度のモデルと一緒に並べてみました。当然ですが、中間のモデルの断面は放物線になります。
製作方法の解説は紹介しませんが、ダウンロードした型紙を使用する場合には以下の点に注意して下さい。
・ 印刷する場合は高解像度で行う。(線が印刷されない可能性があります。)
・ 型紙は各モデル18枚(縦9・横9)。
・ 縦の部品と横の部品を差し込む切り目は、使用する厚紙程度の隙間を持たせる。
実際に計算すると明らかなのですが、全く異なる方法で、以前に作った曲面と同じものができるのは興味深いことです。
