
2013年度 数楽工作倶楽部 第6回製作物
トーラスのスライス
第5回で製作した3次元ハート形のスライスと同様の手法で、数学の世界では「トーラス」とよばれるドーナツ型の立体スライスモデルを製作しました。
随分前に、下のような xy平面と平行な面でスライスしたトーラスを製作したことがありましたが、今回制作するのは、xz平面と平行な面でスライスしたモデルです。

製作前に、トーラスの方程式について簡単に解説します。
下図のように、ドーナツを真上から眺めたとき、外周と内周の中間の円をトーラスの「大円」、ドーナツを直径で切断したときに切り口に現れる円をトーラスの「小円」といいます。
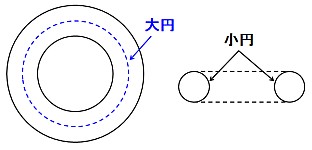
ここでは、大円と小円の半径がそれぞれ「R」と「1」のトーラスを考えることにします。
図のようにドーナツの中心が原点、直径がxy平面上にあるとします。
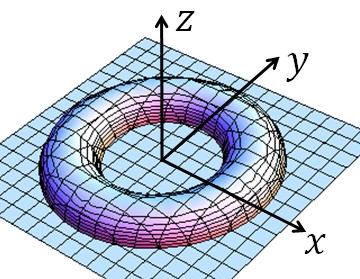
このとき、xz平面上でのドーナツの表面の座標は、左下図のように表すことができます。よって、その点を z = sin s 平面上でドーナツの表面上を動かした点は、右下図のように表されることがわかります。(図はクリックすると拡大します)
従って、トーラスの表面上の点は次のように表されることがわかりました。
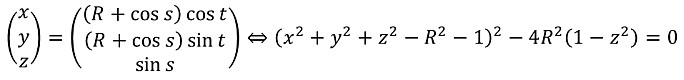
上記の方程式がわかれば、あとは前回製作したハート形の立体と同じ方法で作ることができます。
製作風景(画像をクリックすると拡大します)
前回ハート形を製作した時には、パーツ同士の間隔をあまり厳密に設定しませんでしたが、今回そこをいい加減にすると、完成品を上から眺めた時にドーナツが「円」ではなく「楕円」になってしまうため、部品を0.1mm単位で正確に設計する必要があります。
今回使用した材料は次の通りです:
ケント紙(厚さ約 0.2mm)・・・トーラスの部品
プラ板(厚さ 1.2mm)・・・隙間材
展示ケース(ダイソーで購入)
ケント紙を切り抜いて作った「33枚」のトーラスの断面の間と両端に「34枚」の隙間材と使用するため、完成品の厚さは47.4mmになります。これは、使用する展示ケースにほぼぴったり収まるサイズです。
これらを使い、「z軸方向に0.35移動した大円と小円の半径がそれぞれ2と1のトーラス」と「xy平面」を「-3.5 < x < 3.5,
-3.5 < y < 3.5」の領域に描いた立体を製作しました。
1.部品の切り抜き

A4サイズ型紙DL (余分な長方形の部品が2枚あります)
2.部品を並べる
プラパンと交互に並べてゆきます。固定していないので修正はいつでも可能です。
3.完成
