２０１４年度　数楽工作倶楽部　第１回製作物

双曲面を折る

折り紙で、上のような双曲面を製作してみました。
ネットでも見かける比較的ポピュラーなネタですが、図面の紹介や数学的な解説はあまり見かけないようなので、その部分を含めて製作方法を紹介します。
以前に、針金を使った下の写真のようなモデルを製作したことがありましたが、今回の折り紙のモデルでは、その針金のフレーム部分を紙の「折り目」で再現します。

数学的解説　（図はクリックすると拡大します）

下図のように、ｘｙｚ空間上の2枚の円盤と、円盤上の点Ｐ,Ｑを考えます。

円盤上のＰＱの偏角が等しい場合、２点ＰＱを結んだ直線の軌跡は円筒形になります。
一方、点Ｑの偏角を2αだけ進め、２点を同様に結んだ直線の軌跡は下図のようになります。

2点ＰＱを結んだ直線の方程式を、パラメータｋを用いて表すと

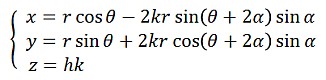
となりますが、ここからｋとθを消去すると次の式が得られます。

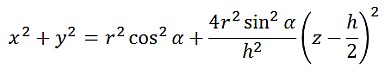
少しわかりやすくするために、ｚ軸方向に−ｈ/２平行移動すると

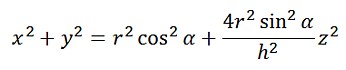
となります。
特に、α＝０、α＝π/２の場合には、それぞれ下のような「円筒」と「円錐」の方程式が得られます。

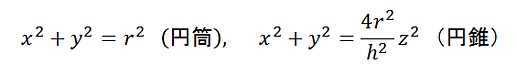
また、ｘｚ平面と平行な平面：ｙ＝ｂでの切断面の方程式は

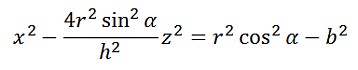
となりますが、これを少し整理すると

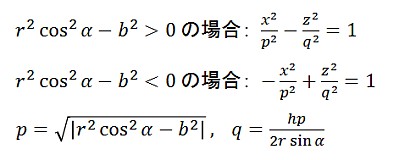
となり、ｘｚ平面上の双曲線であることがわかります。
今回製作するのは、上下それぞれの円周上に等間隔にとった１２点

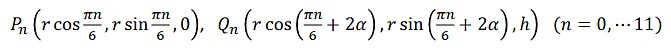
同士を結んだモデルです。

折り紙でこのようなモデルを製作する場合、形状を維持するために「折り目」から成る「三角形」の構造を入れる必要があります。
今回のモデルでは、三角形として

を考えます。すると、基本となる型紙は次のようになります。

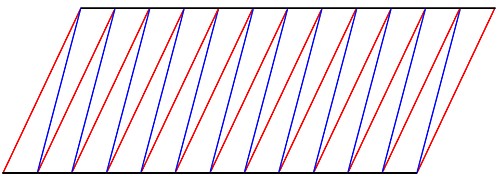
赤線は山折り・青線は谷折り（逆でも可）

では、このような型紙から作られる完成品の形状を計算してみましょう。

円周上の点の数をｎとして、上の図から三角形を一つ取り出してみると、辺の関係は次のようになります。

また、円盤を真横から眺めると

であることに注意すると、次の関係式が成り立つことがわかります。

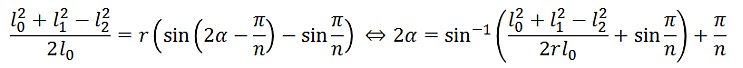
モデルの製作

以下の型紙データをダウンロードして下さい。
型紙（PDFファイル）
使用する紙は、厚紙よりもコピー用紙やトレーシングペーパーのような、薄く折り目がしっかりとつくもの、サイズは「Ａ４」でも可能ですが、より大きな紙の方が作りやすいようです。

１．折り筋をつける
紙を切り出す前に、「ヘラ」や「書けないボールペン」などを使い、点線上にしっかりと折り筋をつけておきましょう。　　

２．実線に部分を切る
実線に沿って切り抜き、さらに実線に切り込みをいれましょう。
中段右端の平行四辺形が、丸めた時に重なる「のりしろ」部分になります。

３．紙を折る
山折り、谷折りに注意しながら、中段の斜めの折り目を交互にしっかりと折ってゆきましょう。

　　

丸くなったら、下の写真を参考に、上下の円盤になる部分を折ってゆきます。
　

４．丸める
丸めて「のりしろ」部分をスティックのりなどで貼り付けましょう。
のりを使わなくても、最終的には形状を維持することができますが、ここではりつけておくと作業がかなり楽になります。

　

下の写真を参考に、円盤部分を織り込んでクリップで留めてゆきます。その際、できるだけ「くびれ」の形状を維持しながら完成させてゆくことがコツです。
組み上げた後に「ねじって」仕上げることも不可能ではないですが、骨格を形成する「折り目」が崩れてしまう場合があります。
　　

５．完成
無事に組み合が得ると、クリップを外しても崩れません。

【注意】
行程４で「くびれがない」立体ができてしまう場合がありますが、実はこれも「正しい完成形」です。
実は、この型紙からは異なる２種類の立体ができる可能性があります。
数学的には、ｌ_0, ｌ_1, ｌ_2 と Ｐ_(n-1), Ｐ_n を与えた時、２次方程式の解として定まるＱ_nの座標が２種類あることを意味します。

Back