２０１５年度　数学工作倶楽部０１

２０１５年度　数楽工作倶楽部　第１回

紙バンドによる多面体編み２

パート１では、６本のバンドを用いて「二十・十二面体」を編みましたが、今度は４本のバンドを使って「立方八面体」と呼ばれる半正多面体を編んでみましょう。

立方八面体

五角形の周りを三角形が囲んでいた「二十・十二面体」に対して、「立方八面体」は四角形の周りを三角形が囲んでいます。パート１の製作手順を参考にすると、立方八面体は次のように簡単に編むことができます。

１．４本のバンドを下の写真のように組み合わせてクリップで固定する。

２．四角形の周りに４個の三角形を作って固定する。

三角形を囲む帯の重なる順序に注意してください。

３．赤と黄色の帯でリングを作る。

下の写真のように糊付けして赤と黄色のリングを作ります。

４．青と緑の帯でリングを作る。

四角形を囲む帯が「きれいな順序」で重なるように、青と緑の帯を赤と黄色のリングの上下を通してリングを作ると完成です。

　

４本のリングで作ったモデルの四角形の穴の一つを広げてゆくと、下の写真のように腕輪のような形になります。

今度は、「多面体」ではなく絡み合ったリングとして、この構造を詳しく見てみることにします。
リングの交差の様子に注目し、上の腕輪を次のように表現してみます。

ここで、上の図に対して次のように考察を行ってみます。

（１）リングの交差が無い上半分は無視する。

（２）横一直線に交差する場所が３段あるので、上から順に１，２，３と番号をつける。

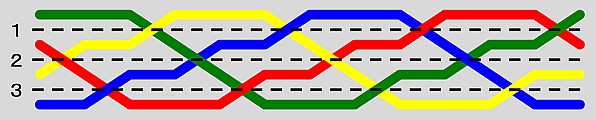
（３）「k 段目」にある、「左下から右上に向かう線が上」になる交差をσ_k と表す。一方、線の上下が反対になる交差をσ_k^-¹ と表す。

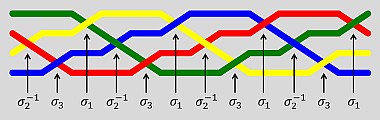
（４）交差を左から順番に並べ、複数の交差を交差の「積」とみなして「べき乗」を用いて次のように表す。

これは、数学の「位相幾何学」の一分野である「結び目理論」で用いられる「ブレイド群」による表現です。

パート１で作ったモデルも（より細い帯で編んで）腕輪の形にして交差の順番を調べてみます。

　

注意深く見ると、上の写真のように σ₅ σ₂^-1 σ₃ σ₄^-1 σ₁ σ₃ が５回繰り返されていることがわかるので、ブレイド群による表示は次のようになります。

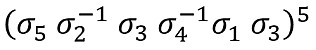
数学者とは、現実に存在する物体や現象を、一般化・抽象化して単純な数式で表現することに喜びを感じる人々です。もしも、

　が　　や　　が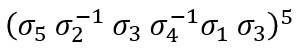　

と表現できることに少しでも面白みを感じることができれば、その人はもう立派な数学者です。