俀丏婡夿岺妛傊偺Newton椡妛偺墳梡嘦
2.1 塣摦偺敪惗丆寛掕梫場丗堦斒揑偵偼丆嶌梡椡丆嶌梡儌乕儊儞僩
丂戜幵偑幬柺傪壓傞尰徾傪尒偰丆暔懱偑壗屘丆戜幵偑幬柺傪壓傞塣摦傪婲偙偡偺偐丠偲偄偆偲丆偳偆摎偊傞偺偱偁傠偆偐丠暔懱偵偼廳椡偑嶌梡偟丆壓岦偒偵乭椡乭偑嶌梡偟偰偄傞偺偱丆幬柺忋偵傕偺傪抲偔偲幬柺偵増偭偰摥偔椡傕敪惗偡傞偺偱丆幬柺偵暯峴側曽岦偵塣摦傪巒傔傞丆偲偄偆偺偼偡偖偵傢偐傞帠偱偁傠偆偐丠
丂儘乕儔乕偑幬柺傪揮偑傝側偑傜丆壓偭偰峴偔偲偄偆応崌偵偼丆乮懡暘乯幬柺偲儘乕儔乕娫偵妸傝偑惗偠偰偄側偄乮偙偲傪幚偼壖掕偟偰偄傞乯偺偱丆儘乕儔乕偵嶌梡偡傞廳椡偵懳偟偰敪惗偡傞幬柺偺斀椡偵斾椺偟偨幬柺偐傜偺椡乮杸嶤椡乯偵傛傞乮椡偺乯儌乕儊儞僩偵傛傝丆儘乕儔乕偼丆廳怱夞傝偵揮偑傝棊偪傞丆偲偄偆夝庍偼惓偟偄偱偁傠偆偐丠
丂
丂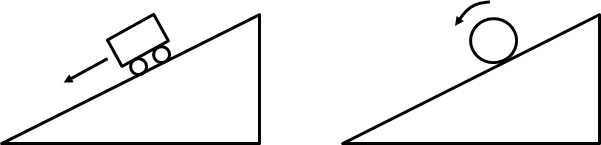
丂恾2-1丂幬柺傪壓傞2偮偺暔懱偵嶌梡偡傞椡偲偼丠
丂
丂偙偆偄偭偨椡偲塣摦丆偁傞偄偼丆儌乕儊儞僩偲夞揮塣摦傪棟夝偡傞偲偄偆帠偼丆Newton偺朄懃傪棟夝偡傞偺偲摨偠嶌嬈偲偄偆偙偲偵側傞丏婡夿僔僗僥儉偵摦嶌乮塣摦乯傪奐巒偝偣傞偨傔偵偼丆椡丆偁傞偄偼丆儌乕儊儞僩傪壛偊傞丆嶌梡偝偣傞偙偲偑昁梫偵側傞偑丆偦偙偵丆壗偐椡偑摥偄偨偳偆偐偼丆幚嵺偵偼丆塣摦傪巒傔傞偐丆偲偐丆曄宍傪婲偙偟偨偐偲偄偆寢壥傪尒傞埲奜偵妋擣偱偒側偄偺偑捠忢偱偁傞丏側偺偱丆椡傪僀儊乕僕偟偰傒偨傝丆椡偑嶌梡偟偰偄傞忬懺傗椡偺嶌梡偵傛傞暔懱偑塣摦偡傞偲偄偆僀儊乕僕傪帩偮偙偲偑傑偢昁梫偱偁傞丏偲偙傠偱丆偙偙偱偄偆乭椡乭傪偳偆偄偆晽偵棟夝偟偨傜椙偄偩傠偆偐丠帿彂傪挷傋偰傒傞偲丆
丂偪偐傜亂椡亃乮怴柧夝崙岅帿揟乯
丂摦暔偑帺暘偱摦偄偰壗偐傪偟丆懠傪摦偐偟偰壗偐傪偝偣傞摥偒偺婎偲偟偰旛偊偰偄傞傕偺丏[暥柆偵傛傝擻椡丒妛椡丒惛恄椡丒懱椡丒朶椡丒尃椡丒惃椡丒埿椡丒帒椡側偳偺堄偵梡偄傜傟丆暔棟妛偱偼廳椡丒堷椡丒埑椡側偳偺傛偆偵暔懱偺埵抲丒忬懺傪曄壔偝偣傞嶌梡偲偟偰婯掕偝傟傞]
塸岅偺帿彂偱挷傋偰傒傞偲丆椡丆儌乕儊儞僩偵偮偄偰偼丆
丂亂force亃PHYSICAL POWER(CAMBRIDGE(International dictionary))
丂乬physical, esp. violent, strength or power乭
丂亂force亃The HUTCHINSON(Dictionary of science)
丂乬any influence that trends to change the state of rest or the uniform motion in a straight line of a body. The action of an unbalanced or resultant force results in the accelelration of a body in the direction of action of the force, or it may, if the body is unable to move freely, result in its deformation. Force is a vector quantity, possessing both magnitude and direction; its SI unit is the newton.乭
丂亂moment of a force亃The HUTCHINSON(Dictionary of science)
丂乬in physics, measure of the turning effect, or torque, producted by a force acting on a body. It is equal to the product of the force and the perpendicular distance from its line of action to the point, or pivot, about which the body will turn. Its unit is the newton metre.乭
偲婰嵹偝傟偰偍傝丆椡帺懱傕Newton偺朄懃偲偺娭楢晅偗偱棟夝偡傞偺偑丆堦斒揑偺傛偆偵巚傢傟傞丏偦偙偱丆Newton偺朄懃偵棫偪栠偭偰傒傞丏
Newton偺戞1朄懃乮姷惈偺朄懃乯
丂暔懱偵椡偑摥偄偰偄側偄偲偒丆暔懱偼摍懍捈慄塣摦傪懕偗傞丏
丂丂$\Rightarrow$丂偳傫側庬椶偺奜椡傕摥偐側偄暔懱偺塣摦傪乮惷巭偟偰偄傞応崌傕娷傔偰乯摍懍捈慄塣摦偲偟偰婰弎偱偒傞嵗昗偑偮偹偵懚嵼偡傞丏
丂丂$\cdots$丂姷惈偺朄懃偑惉傝棫偮嵗昗宯丗姷惈宯
Newton偺戞2朄懃乮塣摦偺朄懃乯
丂椡偑摥偔偲懍搙偼曄壔偟丆偙偺偲偒偺壛懍搙偼椡偺戝偒偝偵斾椺偟丆曽岦丒岦偒偼椡偺曽岦丒岦偒偲摨堦偱偁傞丏
丂丂$\Longrightarrow$丂椡偺掕媊丗暔懱偺塣摦忬懺傪曄壔偝偣傞嶌梡
Newton偺戞3朄懃乮嶌梡丒斀嶌梡偺朄懃乯
丂擇偮偺暔懱偑屳偄偵椡傪媦傏偟偁偆偲偒丆嶌梡偲斀嶌梡偼戝偒偝偑憡摍偟偔丆摨堦捈慄忬偵偁傝丆岦偒偼屳偄偵斀懳偱偁傞丏
婡夿岺妛偑娭傢傞杦傫偳偺懳徾偵懳偟偰丆偙傟傜偺朄懃偑惉傝棫偮偙偲傪擣傔偨偆偊偱乭傕偺偯偔傝乭偑峴傢傟傞偺偱丆偙傟傜偼丆惓偟偄偲偟偰擣傔傞乮怣偠傞乯昁梫偑偁傞丏偦偺偨傔偵偼丆偙傟傜偺朄懃偱憐憸乮栂憐乯偡傋偒塣摦忬懺傗塣摦偵嶌梡偟偰偄傞嶌梡椡丆嶌梡儌乕儊儞僩傪僀儊乕僕偡傞偙偲傕堦彆偲側傞乮偲巚傢傟傞乯丏恾2亅2偵帵偡僥乕僽儖忋偵抲偐傟偨嫵壢彂偼丆壗傕側偔偦偙偵棷傑偭偰偼偄傞偑丆幚嵺偵椡偑嶌梡偰偄傞偲峫偊傜傟傞丏偦偙偵嶌梡偟偰偄傞椡傪僀儊乕僕偡傞偙偲偼偱偒傞偱偁傠偆偐丠
丂
丂
丂恾2-2丂僥乕僽儖忋偵偁傞杮
丂
暔懱偵嶌梡偡傞椡傪僀儊乕僕壔偡傞曽朄偲偟偰丆Free-Body Diagram偑偁傞丏偙傟偼丆扨撈側堦偮側暔懱偵嶌梡偡傞椡媦傃儌乕儊儞僩傪彂偒婰偟偨恾偱偁傝丆偙偺暔懱偵楢寢偡傞傕偺丆偁傞偄偼丆偮側偑偭偰偄傞売強偲偺娫偵偼丆僯儏乕僩儞偺戞俁朄懃偵婎偯偔丆嶌梡椡丆嶌梡儌乕儊儞僩傪僀儊乕僕偡傞偙偲偵側傞丏僯儏乕僩儞偺戞俁朄懃偼丆暔懱摨巑偩偗偱側偔丆暔懱撪晹偱愗抐柺傪峫偊偨応崌傕惉棫偡傞奣擮偱偁傞丏Free-Body Diagram傪棟夝偡傞偨傔偵丆婡夿岺妛暘栰偱梕堈偵憐憸偱偒傞乮偲巚傢傟傞乯帺摦幵偺塣摦傪峫偊偰傒傞
亂Quiz侾亃壛懍搙$\alpha$偱壛懍偟偰偄傞帺摦幵偵嶌梡偡傞椡偼丠
丂恾2-3偼丆帺摦幵偺懁柺偐傜尒偨帺摦幵偵嶌梡偟偰偄傞廳椡偲帺摦幵偺慜椫丆屻椫偱嶌梡偟偰偄傞椡傪僀儊乕僕偟偨傕偺偱偁傞丏
丂
丂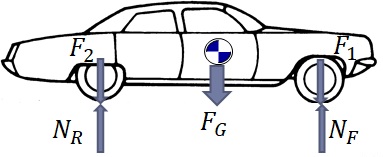
丂恾2-3丂帺摦幵偵嶌梡偡傞廳椡偲偦傟偵敽偆斀椡
丂
抧媴忋偵嫃傞乭恖乭丆偁傞偄偼丆抧媴忋偵偁傞乭傕偺乭偵偼丆墧捈壓岦偒偵乮抧媴偺拞怱偵岦偗偰丆偁傞偄偼丆忋壓曽岦偺壓岦偒偵乯廳椡$F_G$偑嶌梡偡傞乮偙偲偼帠幚偲偟偰擣傔傞偙偲偵偡傞丗枩桳堷椡偺朄懃乯丏恾偺傛偆偵偙偆偄偭偨廳椡偼廳怱偵嶌梡偡傞偲堦斒偵偼峫偊傞丏偙偺廳椡偵傛傝帺摦幵偼壓岦偒偵椡傪庴偗丆傕偟丆慜屻椫僞僀儎偑抧柺偲愙偟偰偄傞偲偡傞偲丆僞僀儎愙怗柺偱抧柺傪墴偡椡偑丆敪惗偡傞乮傛偆偵巚傢傟傞乯丏偦偙偱丆恾偵帵偡傛偆偵丆廳椡偲摨偠曽岦丆懄偪丆
丂墧捈乮忋壓乯曽岦壓岦偒偺椡$F_1$丆$F_2$丗帺摦幵偺幙検偵傛偭偰敪惗偡傞廳椡偵婲場偟偰慜屻椫偺僞僀儎傪夘偟偰楬柺偵嶌梡偡傞椡
傪憐憸乮栂憐乯偡傞偙偲偑偱偒傞乮偐傕偟傟側偄乯丏慜屻椫偺僞僀儎愙怗揰傪峫偊傞偲楬柺偼丆偙偺椡傪捈愙庴偗傞偑丆堦斒偵偼楬柺偼寴偔曄宍偡傞偙偲偼柍偔丆傑偨丆堏摦偡傞偙偲傕柍偄丏恾2亅2偱帵偟偨乭僥乕僽儖忋偵偁傞杮乭偲摨偠偙偲偱偁傞偑丆偙傟傪偳偺傛偆偵峫偊偨傜傛偄偩傠偆偐丠僞僀儎慜屻椫偱楬柺偵懳偡傞嶌梡偼丆愭傎偳峫偊偨$F_1$丆$F_2$側偺偱丆偙偺嶌梡偑懪偪徚偝傟傞傛偆側尰徾偑敪惗偟偰偄傞丆偲峫偊丆椡偼儀僋僩儖偲偄偆奣擮偐傜丆嶌梡揰偑摨偠側偺偱丆偙偺揰偵丆戝偒偝偑摨偠偱曽岦偑斀懳偺椡偑嶌梡偟偰偄傞偲偡傞偲丆尰徾偺愢柧偑偱偒傞乮傛偆偵巚傢傟傞乯丏懄偪丆僯儏乕僩儞偺戞俁朄懃丗嶌梡丒斀嶌梡偺朄懃傪擣傔傟偽丆偙偆偄偭偨尰徾傪愢柧偡傞偙偲偑偱偒丆恾偵帵偡師偺傛偆側椡$N_F$丆$N_R$傪峫偊傞丏
丂墧捈乮忋壓乯曽岦忋岦偒偺椡$N_F$丆$N_R$丗帺摦幵僞僀儎偺慜椫丆屻椫愙抧柺偵偍偄偰丆楬柺偑偦傟偧傟丆慜椫丆屻椫傪墧捈忋岦偒偵墴偡椡
偙偙偱丆$F_1$丆$F_2$偼丆楬柺傊偺嶌梡椡偱帺摦幵帺懱偑楬柺偵壛偊偰偄傞椡偱偁傞偺偵懳偟丆$N_F$丆$N_R$偼丆僞僀儎傪夘偟偰丆楬柺偑帺摦幵偵壛偊偰偄傞椡丆偲偄偆偙偲偑偱偒傞丏
丂峏偵丆悈暯曽岦塃懁偵壛懍搙$\alpha$偱壛懍憱峴偡傞応崌偵敪揥偝偣傞丏帺摦幵偑壛懍偡傞尰徾傪徻偟偔愢柧偟傛偆偲偡傟偽丆僄儞僕儞傗僩儔儞僗儈僢僔儑儞側偳懡偔偺揱払宯乮婡夿梫慺乯偺偟偔傒偵偮偄偰岅傞偙偲傕偱偒傞偑丆偙偙偱偼傾僋僙儖傪摜傓偲僞僀儎偑夞揮偡傞丆埵偵棷傔偰偍偔丏懄偪丆恾2-4嵍恾偵帵偡傛偆偵丆壛懍偟傛偆偲偟偰傾僋僙儖傪摜傓偲僞僀儎偑夞揮傪巒傔傞丏僞僀儎偺夞揮曽岦偲偲楬柺偺悈暯曽岦偺娫偵椡傪揱払偡傞尰徾乮杸嶤側偳乯偑偁傞偲偡傟偽丆僞僀儎偑楬柺傪悈暯曽岦屻傠岦偒乮嵍岦偒乯偵墴偡乮楬柺傪屻傠懁偵墴偟弌偡乯傛偆側椡$F_R$偑敪惗偡傞乮偙偲偼僀儊乕僕偱偒傞偱偁傠偆偐丠乯丏偙偙偱傕丆嶌梡丒斀嶌梡偺朄懃傪擣傔傟偽丆楬柺偼丆媡偵丆僞僀儎傪戝偒偝偑摨偠偱曽岦偑媡丆懄偪丆悈暯曽岦慜岦偒乮塃岦偒乯偵墴偡椡$F$傪峫偊傞偙偲偑偱偒傞乮偲偐傕偟傟側偄乯丏恾2-4塃恾偼丆屻椫嬱摦傪壖掕偟偰丆偙偺嶌梡椡$F$傪娷傔丆乭帺摦幵偵嶌梡偟偰偄傞椡乭傪僀儊乕僕壔偟偨傕偺偱丆嶌梡椡$F$偼丆帺摦幵憱峴偵偍偄偰乭嬱摦椡乭偲屇偽傟丆帺摦幵偺壛懍傪敪惗偝偣傞椡偲偄偆偙偲偵側傞丏
丂
丂 丂丂丂
丂丂丂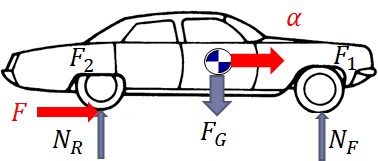
丂恾2-4丂帺摦幵壛懍憱峴帪偵憐掕偝傟傞椡
丂
丂恾2-4塃恾偑丆強堗丆Free-body Diagram偱偁傝丆帺摦幵慡懱偺塣摦傪壛懍搙$\alpha$偱昞偟丆偦偺帪偵帺摦幵偵嶌梡偟偰偄傞椡傪嶌梡揰傗曽岦傪峫偊偰婰弎偟偨僀儊乕僕傪昞偟偨傕偺偱偁傞丏崱夞偺応崌丆塣摦偲娭學側偄偺偱婰弎偟偰偄側偄偑丆楬柺偵嶌梡偟偰偄傞椡傪僀儊乕僕偟偰丆楬柺偵懳偡傞Free-body Diagram傪彂偔偙偲傕偱偒傞乮偑丆楬柺偺応崌偼Free-body偲偼尵偊側偄偐傕偟傟側偄乯丏
丂
亂婡峔宯亃
丂婡夿僔僗僥儉偵偼條乆側椡傪揱払偡傞婡夿梫慺偑巊梡偝傟偰偄傞丏恾2-5偼丆儀儖僩傪巊偭偰儘乕儔乕偵夞揮塣摦傪揱偊傞儀儖僩乗儘乕儔乕宯偱偁傞丏
丂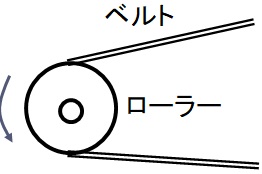
丂恾2-5丂儀儖僩乚儘乕儔乕宯
丂
亂Quiz俀亃儀儖僩偱夞揮偡傞儘乕儔乕偵嶌梡偡傞椡偼丠
丂儀儖僩偵敪惗偡傞挘椡傗儘乕儔乕幉傪幉庴偑墴偡椡乮巟偊偰偄傞丆巟帩偟偰偄傞椡乯傪峫偊偰傒傛偆丏
2.2 塣摦偺椡妛揑昞尰丗僯儏乕僩儞偺戞俀朄懃
丂婘偺忋偵抲偐傟偨杮偺墧捈乮忋壓乯曽岦偺塣摦乮嫇摦乯偵偮偄偰峫偊傞丏杮偺廳怱埵抲偵幙検偑廤拞偟偰偄傞偲偟丆杮傪幙揰偱峫偊傞丏杮偺幙検傪$m$偲偟丆忋岦偒偵$x$嵗昗宯傪庢傝丆壛懍搙傪$a_x$丆懍搙傪$v_x$偲偡傞丏
丂
丂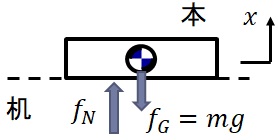
丂恾2-6丂婘偺忋偵抲偐傟偨杮偵嶌梡偡傞椡
丂
恾2-6偵偍偄偰丆廳椡$f_G=mg$丆婘偑杮傪悅捈忋岦偒偵墴偡椡丆悅捈峈椡傪$f_N$偲抲偄偰乮憐掕丆偁傞偄偼丆壖掕偟偰乯偍傝丆Newton偺戞俀朄懃傛傝丆師幃偑惉傝棫偮丏
\begin{eqnarray*}
\frac{d}{dt}\left(mv_x\right)=f_N-f_G=f_N-mg
\end{eqnarray*}
幙検$m$偑帪娫曄壔偟側偄乮偲憐掕偟偰偄傞乯偺偱丆
\begin{eqnarray*}
m\frac{dv_x}{dt}=ma_x=f_N-mg
\end{eqnarray*}
偙偙偱丆$v_x=\dot{x}$丆$a_x={dv_x}{dt}=\ddot{x}$偍傝丆師幃偺塣摦曽掱幃傪摼傞丏
\begin{eqnarray*}
m\ddot{x}=f_N-mg
\end{eqnarray*}
杮偑惷巭偟偰偄傞丆偁傞偄偼丆摉懍搙塣摦偟偰偄傞応崌偼丆$\ddot{x}=0$偲偍偗傞偺偱丆
\begin{eqnarray*}
f_N=mg
\end{eqnarray*}
偲側傝丆悅捈峈椡偼偲廳椡偼掁傝崌偆丆偁傞偄偼丆戝偒偝偑摨偠偱曽岦偑媡偺椡偱偁傞偙偲偑暘偐傞丏
丂師偵丆杮帺懱偵壛懍搙偑惗偠傞忬懺偲偟偰丆杮偑抲偐傟偰偄傞婘偑抧恔側偳偱忋壓偵梙傟偰偄傞応崌傪峫偊傞丏
丂
丂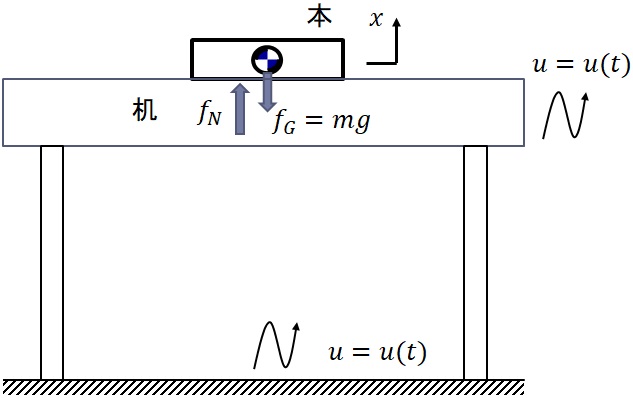
丂恾2-7丂抧恔帪偺婘偺忋偵抲偐傟偨杮偺嫇摦br>
丂
丂婘偑彴偵偟偭偐傝屌掕偝傟偰偄偰丆婘帺懱旕忢偵婃忎偵偱偒偰偄傞偲偡傞偲丆抧柺偑梙傟丆婘偑梙傜偝傟傞偲婘偺忋偵抲偐傟偰偄傞杮傕丆傑偢偼丆婘偲摨偠傛偆偵梙傟傞偼偢偱偁傞丏恾2-7偵帵偡傛偆偵抧柺偑忋壓曽岦偵$u=u(t)$偱梙傟傞偲壖掕偡傞偲丆杮傕摨偠傛偆偵梙傟傞偺偱丆
\begin{eqnarray*}
x=x(t)=u(t)
\end{eqnarray*}
偲側傞丏偙偙偱丆抧恔偺梙傟傪怳暆$A$[m]丆怳摦悢$f$[Hz]偺惓尫攇偱昞尰偱偒傞偲壖掕偡傞偲
\begin{eqnarray*}
u(t)=A\sin2\pi ft
\end{eqnarray*}
偲抲偔偙偲偑偱偒傞丏傛偭偰丆杮偺乭曄埵乭偼師幃偲側傞丏
\begin{eqnarray*}
x=x(t)=u(t)=A\sin2\pi ft
\end{eqnarray*}
帪娫旝暘偟偰丆壛懍搙傪媮傔傞丏
\begin{eqnarray*}
&& \dot{x}=\frac{d}{dt}\left(A\sin2\pi ft\right)=2\pi fA\cos2\pi ft \\
&&\therefore \ddot{x}=-\left(2\pi f\right)^2A\sin2\pi ft
\end{eqnarray*}
偙傟傪塣摦曽掱幃
\begin{eqnarray*}
m\ddot{x}=f_N-mg
\end{eqnarray*}
偵戙擖偟丆悅捈峈椡$f_N$傪幃偱昞偡偲丆
\begin{eqnarray*}
f_N=m\left(g+\ddot{x}\right)=m\left\{g-\left(2\pi f\right)^2A\sin2\pi ft\right\}
\end{eqnarray*}
懄偪丆抧恔偑敪惗偡傞偲丆暔懱偵嶌梡偡傞悅捈峈椡偼丆堦掕偱偼側偔側傞偙偲偑暘偐傞乮摉偨傝慜偐傕偟傟側偄偑乯丏偙偙偱丆
\begin{eqnarray*}
\left|\sin2\pi ft\right|\leqq 1
\end{eqnarray*}
偍傝丆悅捈峈椡$f_N$偼丆師偺娭學傪帩偮偙偲偵側傞丏
\begin{eqnarray*}
m\left\{g-\left(2\pi f\right)^2A\right\}\leqq f_N\leqq m\left\{g+\left(2\pi f\right)^2A\right\}
\end{eqnarray*}
偙偙偱丆$f_N$偺晞崋偵偮偄偰峫偊偰傒傞丏$f_N$偼丆杮偵嶌梡偡傞廳椡偵傛傝丆杮帺懱偑婘傪墴偡偲偄偆嶌梡椡偵懳偟偰丆斀嶌梡椡偲偟偰丆婘偑杮傪墴偟曉偟偰偄傞椡偱偁傞丏廳椡偵婲場偟偰偄傞偨傔丆壓懁偵墴偡偲偄偆椡偟偐惗傒弌偝側偄偺偱丆偦偺斀嶌梡椡偱偁傞$f_N$偼丆媡偵忋懁偵墴偟曉偡偙偲偟偐偱偒側偄丏偦偺偨傔丆$f_N$偑晧偺抣傪庢傞偙偲偼柍偄乮偼偢偱偁傞乯丏懄偪丆$f_N$偑暔棟揑偵堄枴傪帩偮偺偼丆
\begin{eqnarray*}
f_N\geqq 0
\end{eqnarray*}
偺帪偲側傞丏媡偵丆寁嶼忋$f_N<0$偲側偭偨応崌偼丆婘偑墴偟曉偟偰偄傞偺偱偼側偔丆婘偑杮傪堷偭挘傞偙偲偵側傞丏偟偐偟側偑傜丆偦傟偼丆尰徾偲偟偰婲偙傝偊偢丆$f_N=0$偱婘偐傜杮偑棧傟巒傔傞乮晜偒巒傔傞乯偙偲傪堄枴偡傞丏懄偪丆
\begin{eqnarray*}
&& \quad f_N<0 \\
&& \quad m\left\{g-\left(2\pi f\right)^2A\right\}<0 \\
&& \therefore \left(2\pi f\right)^2A > g
\end{eqnarray*}
偺忦審傪枮偨偡偲丆杮偼婘忋偱挼偹偼偠傔丆拡偵晜偄偨傛偆側忬懺傕婲偙傝偊傞偙偲偵側傞丏
亂Quiz俁亃抧恔偺廃攇悢偑60Hz偺偲偒丆暔懱偑旘傃挼偹傞怳摦怳暆偼丠
2.3 偦偺懠偺塣摦偺昞尰丗巇帠丆僄僱儖僊乕丆塣摦検丆椡愊
丂
丂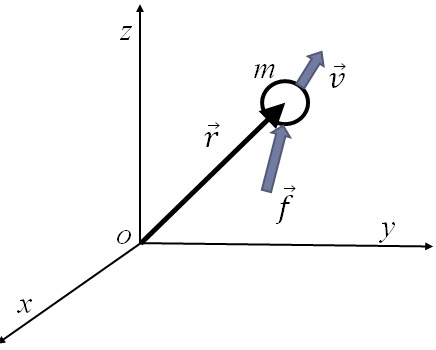
丂恾2-8丂幙揰偲尒側偟偨暔懱$m$偺塣摦偲嶌梡椡
丂
巇帠偲僄僱儖僊乕
丂幙検$m$偺暔懱偑椡$\overrightarrow{f}$傪庴偗偰丆懍搙$\overrightarrow{v}=\frac{d\overrightarrow{r}}{dt}$偱塣摦偡傞偲偒丆Newton偺戞俀朄懃傛傝
\begin{eqnarray*}
\frac{d}{dt}\left(m\overrightarrow{v}\right)=\overrightarrow{f}
\end{eqnarray*}
$\overrightarrow{v}$偲偺撪愊傪庢傞偲
\begin{eqnarray*}
\frac{d}{dt}\left(m\overrightarrow{v}\right)\cdot\overrightarrow{v}=\overrightarrow{f}\cdot\overrightarrow{v}
\end{eqnarray*}
傛偭偰師偺傛偆偵曄宍偡傞偙偲偑偱偒傞丏
\begin{eqnarray*}
&& \quad \frac{m}{2}\frac{d}{dt}\left(\overrightarrow{v}\cdot\overrightarrow{v}\right)=\overrightarrow{f}\cdot\frac{d\overrightarrow{r}}{dt} \\
&& \therefore \frac{1}{2}md\left(\overrightarrow{v}^2\right)=\overrightarrow{f}\cdot d\overrightarrow{r}
\end{eqnarray*}
偙偙偱丆暔懱偑$\overrightarrow{r}_1$偐傜$\overrightarrow{r}_2$偵堏摦偟偨偲偒偵懍搙偑$\overrightarrow{v}_1$偐傜$\overrightarrow{v}_2$偵曄壔偟偨偲偡傞偲
\begin{eqnarray*}
&& \quad \frac{1}{2}m\int_{\overrightarrow{v}_1}^{\overrightarrow{v}_2}d\left(\overrightarrow{v}^2\right)=\int_{\overrightarrow{r}_1}^{\overrightarrow{r}_2} \overrightarrow{f}\cdot d\overrightarrow{r} \\
&& \therefore \frac{1}{2}m\left(\overrightarrow{v}_2^2-\overrightarrow{v}_1^2\right)=\int_{\overrightarrow{r}_1}^{\overrightarrow{r}_2} \overrightarrow{f}\cdot d\overrightarrow{r}
\end{eqnarray*}
塃曈偼丆椡$\overrightarrow{f}$偑側偡巇帠偱偁傝丆嵍曈偼宯偺塣摦僄僱儖僊乕曄壔偲側傞丏偙偺幃偼丆嶌梡椡偵傛傞埵抲偺曄壔傪峫偊丆
丂乽暔懱偵椡傪壛偊偰巇帠傪偡傞偲丆暔懱偺塣摦僄僱儖僊乕偼曄壔偡傞乿
偲夝庍偡傞偙偲偑偱偒丆擬椡妛戞侾朄懃偺峫偊曽偵懳墳偡傞丏
椡愊偲塣摦検
丂Newton偺戞俀朄懃傛傝
\begin{eqnarray*}
&& \quad \frac{d}{dt}\left(m\overrightarrow{v}\right)=\overrightarrow{f}\\
&& \therefore d\left(m\overrightarrow{v}\right)=\overrightarrow{f}dt
\end{eqnarray*}
偙偺応崌偼丆$t_1$偐傜$t_2$偵帪崗偑宱夁偟偨偲偒偺懍搙偑$\overrightarrow{v}_1$偐傜$\overrightarrow{v}_2$偵曄壔偟偨偲偡傞偲
\begin{eqnarray*}
&& \quad \int_{\overrightarrow{v}_1}^{\overrightarrow{v}_2}d\left(m\overrightarrow{v}\right)=\int_{t_1}^{t_2}\overrightarrow{f}dt \\
&& \therefore m\left(\overrightarrow{v}_2 - \overrightarrow{v}_1\right) = \int_{t_1}^{t_2}\overrightarrow{f}dt
\end{eqnarray*}
懄偪丆偙偺応崌偼丆嶌梡椡偺嶌梡帪娫傪峫偊丆
丂乽暔懱偵偁傞帪娫($t_1\sim t_2$)丆椡偑嶌梡偡傞偲暔懱偺塣摦乮検乯偑曄壔偡傞乿
偲偄偆堄枴偲夝庍偱偒傞丏
2.4 椺戣
丂
丂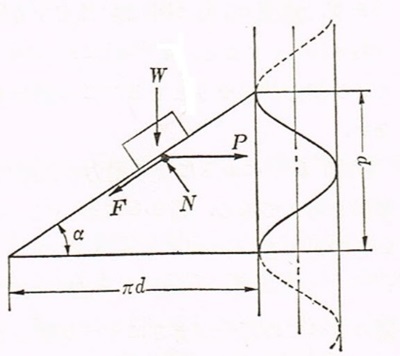
丂恾2-9丂偹偠嶳傪墴偟忋偘傞応崌乮僕儍僢僉乯偵敪惗偡傞椡
丂
丂僕儍僢僉傪梡偄偰丆廳偄傕偺傪帩偪忋偘傞嵺偵僕儍僢僉偺偹偠嶳偵敪惗偡傞椡偵偮偄偰峫嶡偡傞丏僕儍僢僉偱暔懱傪帩偪忋偘傞応崌丆僕儍僢僉偺偹偠嶳偺僺僢僠$p$偲夞揮幉偺桳岠捈宎$d$偱掕傑傞恾2-9偵帵偡幬柺忋傪暔懱廳検乮壸廳乯$W$偵峈偟偰悈暯曽岦椡$P$偱墴偟忋偘偰偄偔忬懺偲峫偊傞偙偲偑偱偒傞丏偙偺墴偟忋偘椡$P$偲壸廳$W$偵懳偟偰丆幬柺忋偺愙怗揰偵偍偄偰偼丆幬柺偵悅捈側曽岦偺悅捈斀椡偲幬柺偵暯峴側峈椡乮杸嶤椡乯偑敪惗偡傞偲峫偊傜傟傞丏恾2-9偵帵偡偲偍傝偱偁傝丆偙偺応崌偺椡偺掁崌偼丆
\begin{eqnarray*}
&& P=N\sin\alpha + F\cos\alpha \\
&& W=N\cos\alpha -F\sin\alpha
\end{eqnarray*}
偲側傞丏備偭偔傝幬柺傪墴偟忋偘丆傎傏懍搙楇偱偁傞偲壖掕偟丆惷巭杸嶤學悢傪$\mu_s$偲偡傞偲丆師幃傪摼傞丏
\begin{eqnarray*}
P=W\frac{\tan\alpha+\mu_s}{1-\mu_s\tan\alpha}
\end{eqnarray*}
幚嵺偵偼丆偙偺椡傪巊偭偰丆桳岠捈宎傪榬偺挿偝偲偟偰丆儌乕儊儞僩傪巊偭偰偹偠傪夞偡偙偲偵側傞丏$\tan\alpha=\frac{p}{\pi d}$傪峫椂偡傞偲丆嶌梡偝偣傞儌乕儊儞僩偼師幃偺傛偆偵昞尰偱偒傞丏
\begin{eqnarray*}
P\cdot\frac{d}{2}=\frac{W\cdot d}{2}\frac{p+\pi d\mu_s}{\pi d-p\mu_s}
\end{eqnarray*}
2.5 墘廗
(1) 墧捈側柺撪偱惓尫嬋慄$y=a\sin\frac{x}{l}$偵増偭偰堦掕懍搙$v$偱摦偄偰偄傞幙検$m$偺幙揰偑嵟掅揰丆嵟崅揰傪捠夁偡傞偲偒偺斀椡傪媮傔傛丏
(2) 墧捈曽岦偵怳摦悢$4$Hz偱挷榓怳摦傪峴偆戜忋偵抲偐傟偨暔懱偑戜偐傜棧傟側偄偨傔偵偼丆戜偺怳暆偼偄偔傜埲壓偱側偗傟偽側傜偸偐丠




 丂丂丂
丂丂丂




