3.機械工学へのNewton力学の応用Ⅲ
3.1 質点の回転運動
下向きに重力(重力加速度を$g$とする)が作用している質点の回転運動について考える.
【例1】
まず,図3-1に示す単振子の運動を考える.
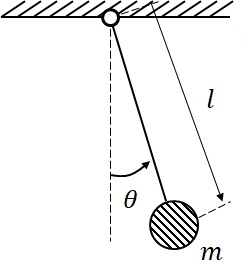
図3-1 単振子の運動
【Quiz 1】単振子の質点に対するFree-body Diagramはどうなる?
単振子を構成要素として,図3-2のように,質量$m$の物体と長さ$l$の糸と支点の固定部(天井)に分けることができる.一般にこの物体は支点位置から距離$l$の位置にある質点と見なし,その質点をぶら下げている糸は質量が無視でき,張力のみが発生し,伸びないことが仮定される.そうすると各部分に作用(発生)している力のイメージは,図3-2に示す矢印のようになり,作用力は,張力$T$と重力$mg$となる.ここで,矢印の方向で力の作用方向(符号)を表している.
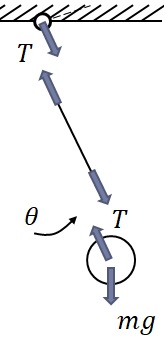
図3-2 単振子のFree-body Diagram例
極座標系で運動方程式を表すことにする.$(r,\theta)$座標系に対して,単位ベクトルを$\overrightarrow{e}_r$,$\overrightarrow{e}_\theta$とすると,位置ベクトル$\overrightarrow{r}$は次のようになる.
\begin{eqnarray*}
\overrightarrow{r} = l \overrightarrow{e}_r
\end{eqnarray*}
よって,速度ベクトルは
\begin{eqnarray*}
\overrightarrow{v} = \frac{d\overrightarrow{r}}{dt}= l \dot{\overrightarrow{e}}_r
\end{eqnarray*}
直交座標系$x$軸,$y$軸方向に対応する単位ベクトルをそれぞれ$\overrightarrow{i}$,$\overrightarrow{j}$とすると次式の関係が成立する.
\begin{eqnarray*}
\left.\begin{array}{l}
\overrightarrow{e}_r =\overrightarrow{i}\cos\theta + \overrightarrow{j}\sin\theta \\
\overrightarrow{e}_\theta =-\overrightarrow{i}\sin\theta + \overrightarrow{j}\cos\theta
\end{array}\right\}
\end{eqnarray*}
$\overrightarrow{i}$,$\overrightarrow{j}$は,時間的に変化しないので,時間微分すると次式を得る.
\begin{eqnarray*}
\left.\begin{array}{l}
\dot{\overrightarrow{e}}_r =\dot{\theta}\left(-\overrightarrow{i}\sin\theta + \overrightarrow{j}\cos\theta\right)=\dot{\theta}\overrightarrow{e}_\theta \\
\dot{\overrightarrow{e}}_\theta = \dot{\theta}\left(-\overrightarrow{i}\cos\theta - \overrightarrow{j}\sin\theta\right)=-\dot{\theta}\overrightarrow{e}_r
\end{array}\right\}
\end{eqnarray*}
よって,
\begin{eqnarray*}
\overrightarrow{v}=l\dot{\theta}\overrightarrow{e}_\theta
\end{eqnarray*}
更に,時間微分して加速度ベクトルは次のようになる.
\begin{eqnarray*}
\overrightarrow{a}&=&\frac{d\overrightarrow{v}}{dr}=l\ddot{\theta}\overrightarrow{e}_\theta+l\dot{\theta}\dot{\overrightarrow{e}}_\theta \\
&=& -l\dot{\theta}^2\overrightarrow{e}_r + l\ddot{\theta}\overrightarrow{e}_\theta = a_r\overrightarrow{e}_r + a_\theta\overrightarrow{e}_\theta
\end{eqnarray*}
即ち,$r$方向,$\theta$方向の加速度成分$a_r$,$a_\theta$は,それぞれ,$-l\dot{\theta}^2$,$l\ddot{\theta}$となる.
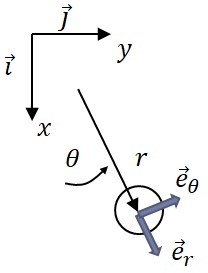
図3-3 単振子に対する極座標表示
図3-2のFree-body Diagramを元に$(r,\theta)$座標系に対してNewtonの第2法則を適用すると
\begin{eqnarray*}
\left.\begin{array}{l}
ma_r = mg\cos\theta - T \\
ma_\theta = -mg\sin\theta
\end{array}\right\}
\end{eqnarray*}
\begin{eqnarray*}
\therefore
\left.\begin{array}{l}
-ml\dot{\theta}^2 = mg\cos\theta - T \\
ml\ddot{\theta} = -mg\sin\theta
\end{array}\right\}
\end{eqnarray*}
即ち,次の2式を得る.
\begin{eqnarray*}
\left.\begin{array}{l}
T = m\left(g\cos\theta + l\dot{\theta}^2\right) \\
l\ddot{\theta} + g\sin\theta =0
\end{array}\right\}
\end{eqnarray*}
運動は第2式のみで定まり,第1式はその運動で定まる張力$T$を規定する条件となる.このように単振子の運動は,二次元の$(x,y)$平面の運動であるが,$(r,\theta)$座標系で考えると,$\theta$座標系のみで表現される1自由度系の運動となることが分かる.また,その運動は(よく知られているように)$l$と$g$で特徴が定まることが分かる.
【例2】
図3-4は,支点$O$回りの自由に回転できる棒Aの両端に質点$m_1$,$m_2$が取り付けられている系を表し,棒Aは質量が無視でき,変形しないと仮定する.$m_1$に上向きに力$f_1$を作用させたときの系の運動を考える.
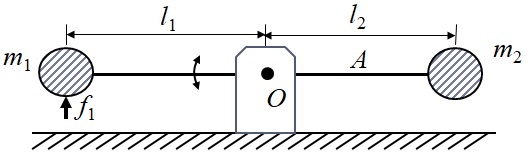
図3-4 両端に質量を持つ棒の支点回りの運動
【Quiz2】図3-4に対応する系に対してFree-body Diagramを示せ.
この系は,支点回りに回転運動をするが,ひとまず,左側の質量$m_1$の変位を力$f_1$に対応させて,上向き$x_1$とする.これに対し,反対側にある質量$m_2$は,支点回りの回転で下向きに変位すると考えられるので,その変位を下向きを正に$x_2$と考えてみることにする.
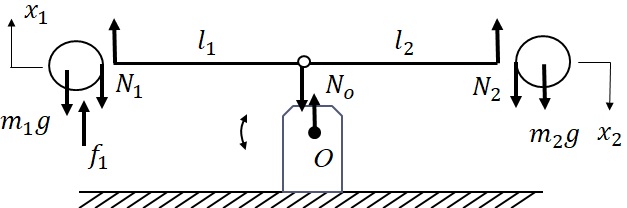
図3-5 支点回りの運動に対するFree-body Diagram
2つの質量,棒,支持部に存在する連結部に発生する力を考える.図に示すように
\begin{eqnarray*}
\begin{array}{ll}
N_1\text{, }N_2 & \text{:棒と各質点間に働く作用・反作用力}\\
N_0 & \text{:支持点での作用・反作用力}\\
m_1g\text{, }m_2g & \text{:重力}
\end{array}
\end{eqnarray*}
と置くと,Newtonの第2法則より,次の運動方程式を得る.
\begin{eqnarray*}
\left.\begin{array}{l}
m_1\ddot{x}_1 = f_1 - N_1 - m_1g \\
m_2\ddot{x}_2 = N_2 + m_2g
\end{array}\right\}
\end{eqnarray*}
また,棒に作用している力の釣合から
\begin{eqnarray*}
0= N_1 -N_0 + N_2
\end{eqnarray*}
また,点O回りのモーメントの釣合いから
\begin{eqnarray*}
&& 0 = l_1\times N_1 - l_2\times N_2 \\
&& \therefore N_2 = \frac{l_1}{l_2}N_1
\end{eqnarray*}
よって,運動方程式の第2式より
\begin{eqnarray*}
m_2\ddot{x}_2 = \frac{l_1}{l_2}N_1 + m_2g
\end{eqnarray*}
\begin{eqnarray*}
\therefore N_1 = \frac{l_2}{l_1}m_2\left(\ddot{x}_2-g\right)
\end{eqnarray*}
これを第1式に代入する.
\begin{eqnarray*}
m_1\ddot{x}_1=f_1 - m_1g -\frac{l_2}{l_1}m_2\left(\ddot{x}_2 - g\right)
\end{eqnarray*}
\begin{eqnarray*}
\therefore m_1\ddot{x}_1 + \frac{l_2}{l_1}m_2\ddot{x}_2 = f_1 + \left(\frac{l_2}{l_1}m_2-m_1\right)g
\end{eqnarray*}
両辺に$l_1$をかけると次式となる.
\begin{eqnarray*}
\therefore m_1l_1\ddot{x}_1 + m_2l_2\ddot{x}_2 = l_1f_1 + \left(m_2l_2-m_1l_1\right)g
\end{eqnarray*}
ここで,点O周りの回転角を時計回りを正として$\theta$とすると,$x_1$,$x_2$は次のように表現できる.
\begin{eqnarray*}
&& x_1 = l_1\theta \\
&& x_2 = l_2\theta
\end{eqnarray*}
よって,この系の運動方程式は次のようになる.
\begin{eqnarray*}
\left(m_1l_1^2 + m_2l_2^2\right)\ddot{\theta} = l_1\times f_1 + l_2\times m_2g - l_1\times m_1g
\end{eqnarray*}
上式において
\begin{eqnarray*}
I_0 = m_1l_1^2 + m_2l_2^2 \text{:点O回りの慣性モーメント}
\end{eqnarray*}
\begin{eqnarray*}
M_O=l_1\times f_1 + l_2\times m_2g - l_1\times m_1g\text{:点O回りに作用している力のモーメントの和}
\end{eqnarray*}
を考えると,運動方程式は次式となる.
\begin{eqnarray*}
I_O\ddot{\theta} = M_0
\end{eqnarray*}
つまり,並進運動のおけるNewtonの第2法則に対応する,回転運動にかける関係を考えることができる.
\begin{eqnarray*}
\begin{array}{ccc}
m\ddot{x}=f & \longleftrightarrow & I_O\ddot{\theta} = M_O \\
\frac{d}{dt}\left(mv\right) & \longleftrightarrow & \frac{d}{dt}\left(I_O\omega\right) = M_0
\end{array}
\end{eqnarray*}
但し,$v=\dot{x}$,$\omega=\dot{\theta}$である.物理量としては,質量に対して慣性モーメント,加速度に対して角加速度,運動量に対して,角運動量を定義できる(理解する必要がある).
ここで,質点系の慣性モーメントは支点,あるいは,回転中心Oから各質点までの距離の2乗に質量をかけた総和
\begin{eqnarray*}
I_O=\sum^i m_il_i^2
\end{eqnarray*}
により定まる.また,力のモーメントは,支点Oからの距離とその垂直力の力の積(力と支点からの垂直距離の積)の和
\begin{eqnarray*}
M_O=\sum^i l_i\times f_1
\end{eqnarray*}
で求められる.
【Quiz3】単振子を支点回りの回転運動と考え,運動方程式を導くとどうなるか?
支点回りの慣性モーメント,および,支点回りのモーメントの和を考える.
3.2 剛体の回転運動
図3-6に示すように,質量$m$,長さ$a$の細長い一様な棒の左端(点Oとする)を滑らかな台上に置き,右端を手で支えた状態から急に手をはなす問題を考える.最初,棒は水平の位置にあると仮定し,左端は台に接したまま重力(重力加速度$g$)の影響を受け運動するとし,水平,垂直方向に$x$,$y$座標を取り,時計回りの回転角変位を$\theta$とする.
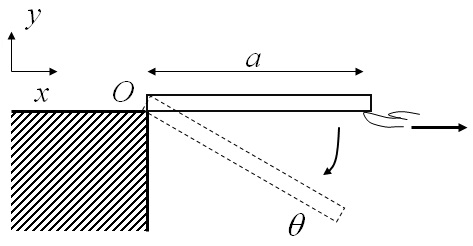
図3-6 剛体棒の回転運動
点O回りの回転運動となるので,点O回りの慣性モーメント$I_O$を定める必要がある.
【Quiz4】質量$m$,長さ$a$の細長い一様な棒の慣性モーメントは?
慣性モーメントの定義は,剛体のように質量が分布している場合は,支点からの距離$r$にある微小質量$dm$を剛体全体わたって質量で積分するという次式で表現できる.
\begin{eqnarray*}
I = \int_m r^2 dm
\end{eqnarray*}
今回の場合,細長い一様な棒,という仮定から,この棒の単位長さ辺りの質量,即ち線密度$\rho$を考えると,$\rho=\frac{m}{a}$とおくことができる.
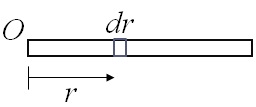
図3-6 細長い一様な棒の慣性モーメント
よって,図3-6に示すように支点Oから$r$距離離れた微小長さ$dr$の部分の質量は$\rho dr=dm$となる.また,積分は支点Oから棒の長さ$a$に亘って行うことになる.即ち,この場合の点O回りの慣性モーメントは次のように計算される.
\begin{eqnarray*}
I_O = \int_mr^2dm=\int_0^a r^2 \rho dr = \int_0^a r^2 \frac{m}{a}dr = \frac{m}{a}\int_0^a r^2 dr = \frac{m}{3}a^2
\end{eqnarray*}
次に運動方程式を求める.この系のFree-body Diagramは図3-7のようになる.ここで,台から棒に作用する垂直抗力を$N$として,重力$mg$は,一様な棒であることから,棒の中心に作用する.よって,棒の重心位置$(x_G,\ y_G)$と回転角$\theta$に対して,運動方程式は次のようにあらわされる.
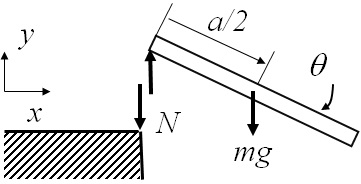
図3-7 剛体棒に対するFree-body Diagram例
\begin{eqnarray*}
\left.\begin{array}{l}
m\ddot{x}_G = 0 \\
m\ddot{y}_G = N - mg \\
\frac{m}{3}a^2\ddot{\theta} = \frac{a}{2}\cos\theta\times mg
\end{array}\right\}
\end{eqnarray*}
第3式より
\begin{eqnarray*}
\ddot{\theta} =\frac{3g}{2a}\cos\theta
\end{eqnarray*}
手を放した瞬間は,点O回りに棒は回転すると考えられるので,重心位置は回転角を用いて次のように表現できる.
\begin{eqnarray*}
\left.\begin{array}{l}
x_G=\frac{a}2\cos\theta \\
y_G=\frac{a}2\sin\theta
\end{array}\right\}
\end{eqnarray*}
時間で微分する.
\begin{eqnarray*}
\left.\begin{array}{l}
\dot{x}_G=-\frac{a}2\dot{\theta}\sin\theta \\
\dot{y}_G=\frac{a}2\dot{\theta}\cos\theta
\end{array}\right\}
\end{eqnarray*}
更に,もう一回微分して加速度を求める.
\begin{eqnarray*}
\left.\begin{array}{l}
\ddot{x}_G=-\frac{a}2\ddot{\theta}\sin\theta-\frac{a}2\dot{\theta}^2\cos\theta \\
\ddot{y}_G=\frac{a}2\ddot{\theta}\cos\theta-\frac{a}2\dot{\theta}^2\sin\theta
\end{array}\right\}
\end{eqnarray*}
運動方程式に代入すると次式を得る.
\begin{eqnarray*}
\left.\begin{array}{l}
\ddot{\theta}\sin\theta+\dot{\theta}^2\cos\theta =0 \\
N = mg+\frac{ma}2\left(-\ddot{\theta}\cos\theta+\dot{\theta}^2\sin\theta\right)
\end{array}\right\}
\end{eqnarray*}
$\ddot{\theta}$を消去してみると,
\begin{eqnarray*}
\left.\begin{array}{l}
\frac{3g}{2a}\sin\theta\cos\theta+\dot{\theta}^2\cos\theta =0 \\
N = mg+\frac{ma}2\left(-\frac{3g}{2a}\cos^2\theta+\dot{\theta}^2\sin\theta\right)
\end{array}\right\}
\end{eqnarray*}
第1式より
\begin{eqnarray*}
\cos\theta\left(\frac{3g}{2a}\sin\theta+\dot{\theta}^2\right) =0
\end{eqnarray*}
$\theta\neq \frac{\pi}{2}$なら
\begin{eqnarray*}
\frac{3g}{2a}\sin\theta+\dot{\theta}^2 =0
\end{eqnarray*}
この時の台からの反力は次のようになる.
\begin{eqnarray*}
N = mg-\frac{ma}2\left(-\frac{3g}{2a}\cos^2\theta+\frac{3g}{2a}\sin^2\theta\right)=mg-\frac{3}4mg = \frac{mg}4
\end{eqnarray*}
手を支えている状態の時は,$N=frac{mg}2$であるが,手を放した瞬間から台からの反力は$\frac{mg}4$に変化する,という結果が得られる.
3.3 角運動量
Newtonの第2法則をベクトルで表すと
\begin{eqnarray*}
\overrightarrow{f} =m\frac{d\overrightarrow{v}}{dt}
\end{eqnarray*}
位置ベクトル$\overrightarrow{r}$との外積を取ると
\begin{eqnarray*}
\overrightarrow{r}\times\overrightarrow{f} =m\overrightarrow{r}\times\frac{d\overrightarrow{v}}{dt}
\end{eqnarray*}
ここで,
\begin{eqnarray*}
\frac{d}{dt}\left(\overrightarrow{r}\times m\overrightarrow{v}\right)&=&\frac{d\overrightarrow{r}}{dt}\times m\overrightarrow{v} + \overrightarrow{r}\times m\frac{d\overrightarrow{v}}{dt}\\
&=& \overrightarrow{v}\times m\overrightarrow{v} + \overrightarrow{r}\times m\frac{d\overrightarrow{v}}{dt} \\
&=& \overrightarrow{r}\times m \frac{d\overrightarrow{v}}{dt}
\end{eqnarray*}
よって,次式の形で表現できる.
\begin{eqnarray*}
\overrightarrow{r}\times\overrightarrow{f} =\frac{d}{dt}\left(\overrightarrow{r}\times m\overrightarrow{v}\right)
\end{eqnarray*}
このとき,左辺は,力のモーメントであり,右辺は,角運動量の時間微分を表している.
3.4 演習
(1) 図に示す質量$m$,半径$r$の半円板を点Oを支点として振子運動させる.その運動を考えるのに必要な重心位置$r_g$と点O回りの慣性モーメント$I_G$を求めよ.
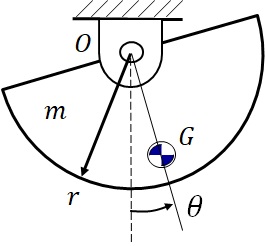
図3-8 半円板の重心と慣性モーメント
(2) 考えている長さ$a$の剛体棒が細長いわけではなく厚さ$b$である場合の慣性モーメントを求めよ.
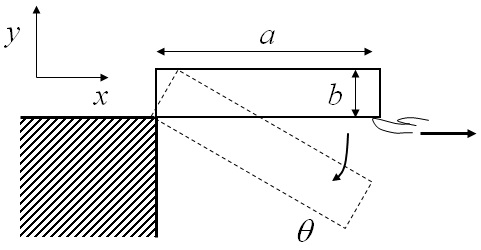
図3-9 剛体棒の慣性モーメント










