5.減衰のない場合の1自由度系の自由振動Ⅰ
5.1 モデル化とモデル化の例
自動二輪,あるいは,乗用車が路面を走行すると車体のみならず,ハンドル部やシート部に様々な振動が発生する(のではないかという)ことが予想される.その現象を調べるには様々な条件で走行させて,実際に走行データを測定し調べるのが手っ取り早いが,車種が変わったらとか想定される走行条件を変えたらとか実験条件には限りがない.そのため,様々な条件を計算上任意に設定できるようなモデルを使って,振動を含む動的な現象を調べる,ということがしばしば行われる.そのモデルで予想される現象から実現象を理解することができたり,走行中に発生する問題を改善するような手立てを考えることができれば,設計への応用も可能となる.
【QUIZ 1】自動二輪や自動車の振動のモデルとはどんなモデルが考えられるであろうか?
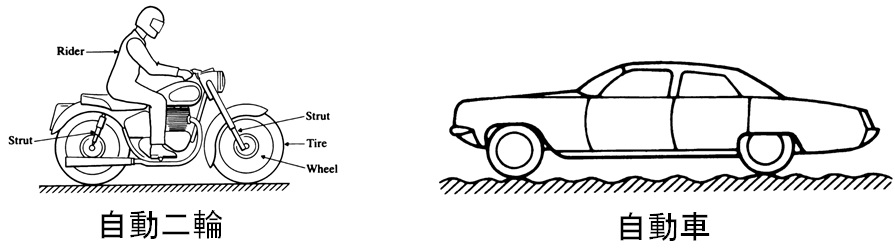
図5-1 乗物のモデル化
機械力学Ⅰでは,対象となる機械,あるいは,機械システム,あるいは,機械構造体について,その質量は重心に集中して存在する仮定して考える.さらに,対象物体の(弾性)変形をHookeの法則が成り立つばねで表現できると仮定してその運動を調べるのが常である.即ち,自動二輪,乗用車のモデルは,例えば図5-2に示すように,重心位置に質量$m$が集中しており,サスペンション,タイヤ等の弾性変形をばね定数$k$のばねで表現できるとして,上下方向の変位を考えることにより,その振動現象を調べる.
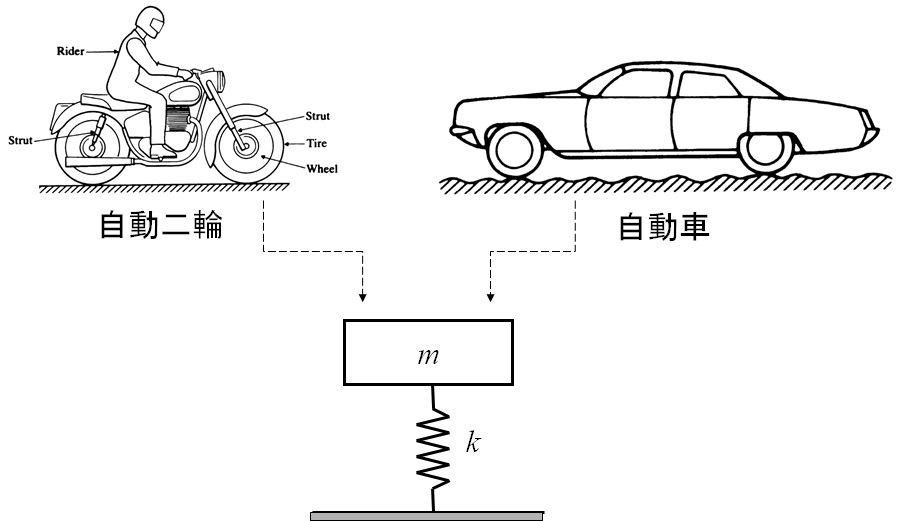
図5-2 乗物の1自由度振動系でのモデル化
【QUIZ 2】高い建物の揺れを調べるモデルはどんなモデルになるか?
高層ビルなどの高い建物は,地震や風荷重などで横揺れすることが予想される.こういった振動を調べる場合も同じように考えることができる.ビルの重心位置に質量が集中しているとして,建物の横方向の変形を弾性的な変形でモデル化すると,図5-3のようになる.即ち建物の重心がある位置に質量$m$が集中して存在し,横方向の変形に対してばね定数$k$のばねでモデル化することになる.
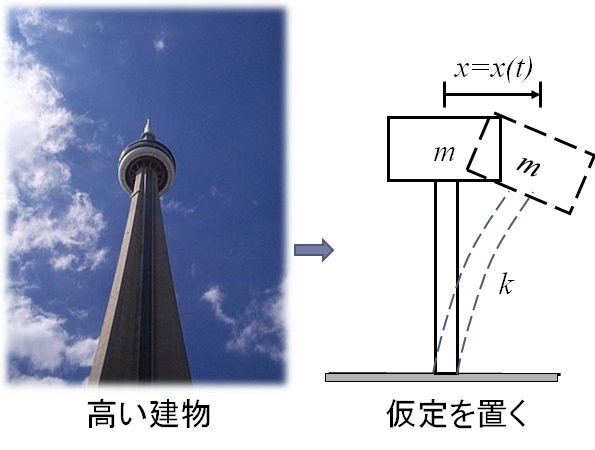
図5-3 高い建物の横揺れのモデル化
この場合は,図5-4右図に示すように,水平(左右)方向の運動に対応する変位$x$を考え,ばねが横向きに連結したモデルを考えることができる.
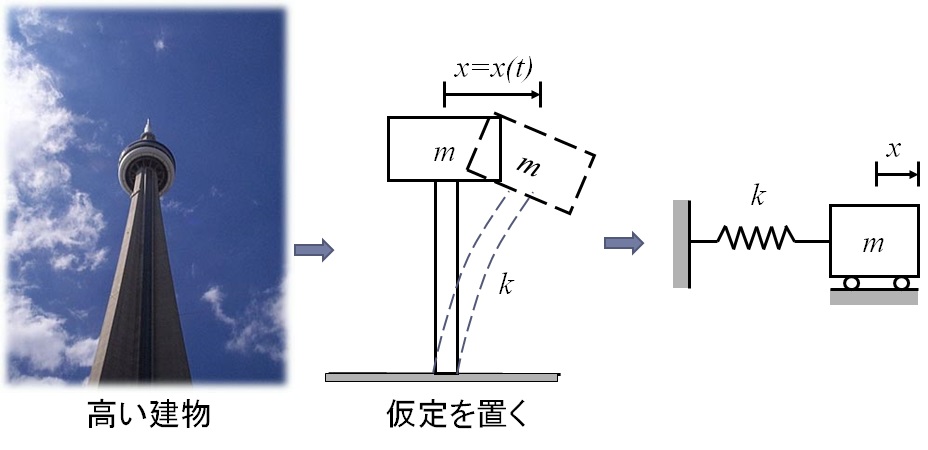
図5-4 高い建物の横揺れの1自由度振動系でのモデル化
同様に,図5-5に示す柔軟なフレーム構造のように横揺れが生じる(可能性のある)構造物なども,重心位置に質量$m$を集中させ,フレーム構造の横方向の変形に対応したばね定数$k$を持つ,ばねで水平方向に支持したモデルを考えることができる.
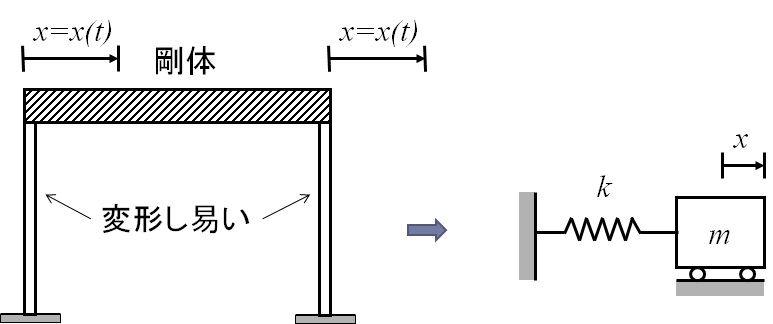
図5-5 柔軟なフレーム構造のモデル化
5.2 1自由度系モデル
対象物体を図5-6に示すように重心位置に質量$m$の質点とそれをばね定数$k$のばねで壁と連結されたモデルで考え,原点から$x$変位した状態の運動方程式を導出し,それを使って振動特性について調べることになる.ここで,運動方程式を導出に当たり,モデル化の際に考慮した事柄とこれまで説明したことの関係は,
〇座標系:変位方向(この場合は水平方向,あるいは,左右方向)に$x$を定義
〇ニュートンの第2法則:物体の質量$m$の動的な特性を定義
〇フックの法則:物体の変形をばね定数$k$で定義
〇作用・反作用の法則:連結部(質量とばね,ばねと壁など)の力学特性を記述
であり,これらの関係を用いて運動方程式を導くことができる.$x$の変位により,ばねは自然長からこの変位分伸ばされたとする.物体とばね,およびばねと壁を別々に取り,作用・反作用の関係で発生している(と考えられる)力を記述すると図5-7のようになる.
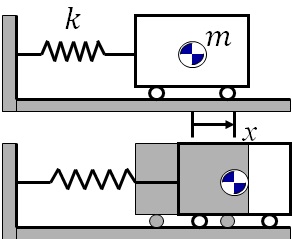
図5-6 1自由度振動系
図に示すように,作用・反作用の法則に基づき連結部で発生する力に関して,分かり易くするために(わざと)変位方向$x$と同じ方向の力を正,逆向きの力を負として表しており,
$+f_1$:壁がばねから受ける力で,ばねが壁を引っ張る力
$-f_1$:ばねが壁から受ける力で,壁がばねを引っ張り返す力
$+f_2$:ばねが物体から受ける力で,物体がばねを引っ張る力
$-f_2$:物体がばねから受ける力で,物体がばねによって引っ張り返される力
となる.ここで,考えたばねの質量は無視することができるとして,ばねに対してニュートンの第2法則を適用する.ニュートンの第2法則は,”ばねの持つ運動量の時間変化は,ばねに作用している力の和がと等しい”,あるいは,質量が変化しない場合は,”質量と加速度の積は,ばねに作用している力の和と等しい”ということになる.しかしながら,質量が零であるので,運動量は零であり,その時間変化も零となることから,次の関係となる.
\begin{eqnarray*}
&& 0= -f_1 + f_2\\
&& \therefore f_2=f_1
\end{eqnarray*}
となる.
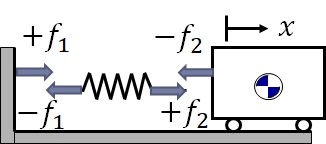
図5-6 1自由度振動系における発生力
当然の結果であるが,ばねの質量が無視できる場合は,ばね自体にも作用・反作用法則と同様に”大きさが同じで方向(符号)が逆の力が発生する”という関係が成り立つことになる.作用・反作用の法則が成り立つ場合,大きさが同じで方向が逆となることから,矢印の方向を正負に対応させ大きさのみを記述することで,発生力を描写することもできる.即ち,1自由度振動系モデルにおいて,質量,ばね,壁(構成要素)に発生している力を図5-7のように描写することができる.このように分解された要素に対して作用する力のイメージを表示した図をFree-body Diagramとも呼び,モデル化された物体の運動方程式を考える際によく利用される.
図中の$f_1$は,上で述べたようにばねを引っ張る力で,ばねの伸び$\Delta s$は,基準の位置(この場合は零)からの移動量となるので,$\Delta s=x-0=x$となるので,フックの法則から
\begin{eqnarray*}
f_1 = kx
\end{eqnarray*}
となる.ばねの右端を右向きのこの力で引っ張り,左端は左向きにこの力で引っ張り$x$だけ伸びていると考えると,質量$m$にかかっている力$f_1$は,右端の力の反作用力であるので,左向きにこの力がかかることになり,壁はばねから右向きにこの力で引っ張られている,ということを表すと考えることができる.よって,図5-7のFree-body Diagramを用いて,質量$m$の物体に,ニュートンの第2法則を適用すると次式となる.
\begin{eqnarray*}
&& m\ddot{x}= -f_1 = -kx \\
&& \therefore m\ddot{x} + kx=0
\end{eqnarray*}
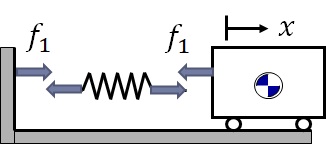
図5-7 1自由度振動系にFree-body Diagram
変形としてばねが伸びる場合を想定したが,ばねが圧縮されて縮む場合について同様に考えてみる.図5-8(a) に示すように,質量$m$の変位によりばねが圧縮する場合は,ばねには物体と壁から圧縮力が作用し,その反力が物体と壁にそれぞれ作用する.そのイメージを示したのが図5-8(b)である.ばねの圧縮に要する力は,$f_1=kx$となるので,物体に対する運動方程式は,
\begin{eqnarray*}
&& m\ddot{x}= -f_1 = -kx \\
&& \therefore m\ddot{x} + kx=0
\end{eqnarray*}
となり,引張力が作用する場合と同じ方程式となる.
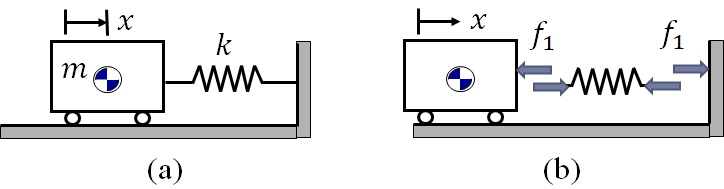
図5-8 1自由度振動系(ばねが圧縮する場合)
同じ場合について,ばねに引張力が作用していると仮定して運動方程式を導出してみる.この場合のFree-body Diagramは図5-9(b)のようになり,ばね力は物体の変位方向と同じ方向なので正符号となる.この時,ばねは引っ張られるので,ばねは伸びるとして,伸び量$\Delta s$を見積もる必要がある.この場合伸びは,ばねの右端の移動量と左端の移動量の差となるので,$\Delta s=0-x=-x$となり,引張力は$f_1=k\Delta s=-kx$となる.即ち運動方程式は次のように定まることになる.
\begin{eqnarray*}
&& m\ddot{x}= f_1 = -kx \\
&& \therefore m\ddot{x} + kx=0
\end{eqnarray*}
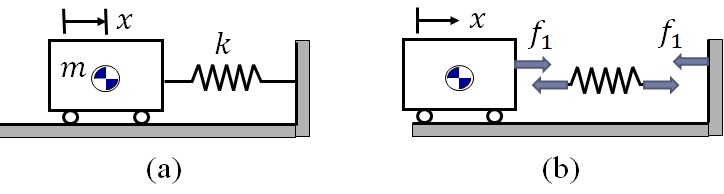
図5-9 1自由度振動系(引張力と考えた場合)
ばね要素に対する発生力をFree-body Diagramで描く場合に,引張力,圧縮力どちらで記載しても構わないが,物体にかかる力と物体からばねにかかる力を見誤らないようにする必要がある.材料力学や弾性力学などで応力,歪に関しは,引張に対応するものを正とするのが常道であるので,本講義では,ばねに対して(基本的に)引張力が作用し,その反力が接続物体(物体,壁など)に作用するとしてFree-body Diagramを記述することにする.
更に,図5-10(a)に示す上下方向変位の振動系において下向きの重力が作用する場合を考える.Free-body Diagramは図(b)のようになり,$f_1=kx$なので,運動方程式は次のようになる.
\begin{eqnarray*}
&& m\ddot{x}= -f_1 -mg = -kx-mg \\
&& \therefore m\ddot{x} + kx= -mg
\end{eqnarray*}
ここで,図5-10(a)の状態で静的な釣り合い状態を考えると,$\ddot{x}=0$なので,
\begin{eqnarray*}
&& kx= -mg \\
&& \therefore x=-\frac{mg}{k}\equiv -\delta
\end{eqnarray*}
となり,静的な釣り合い位置が原点とならないことが分かる.これは,質量$m$の物体をばね定数$k$のばねに載せた場合は,ばねは自然長から$\delta=mg/k$だけ縮み,重力と釣り合う位置で静止するということを意味している.即ち,静的な釣り合い状態までのばねの縮み分が元に戻りさらに$x$伸びたことになるので,ばねの発生力は
\begin{eqnarray*}
f_1=k\left(x-\delta\right)=k\left(x-\frac{mg}{k}\right) = kx -mg
\end{eqnarray*}
となる.よって運動方程式は次のようになる.
\begin{eqnarray*}
&& m\ddot{x}= -f_1 -mg = -kx + mg -mg = -kx \\
&& \therefore m\ddot{x} + kx= 0
\end{eqnarray*}
即ち,静的な釣り合い状態を原点とする運動方程式は,重力が作用しない場合の運動方程式と同じになる.
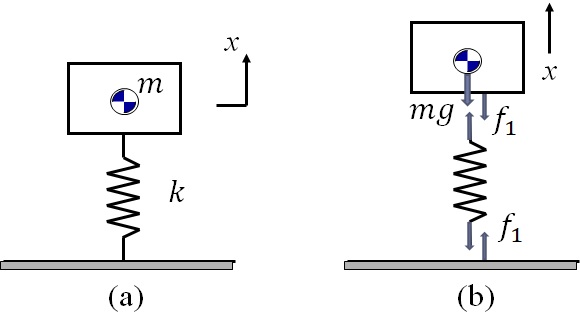
図5-10 1自由度振動系(重力の処理)
5.3 1自由度系振動モデルの解(固有角振動数・自由振動)
得られた運動方程式
\begin{eqnarray*}
m\ddot{x}+ kx =0
\end{eqnarray*}
は,定数係数の常微分方程式であるので,その解法にしたがって解を求めることにする.$m$で割ると
\begin{eqnarray*}
\ddot{x}+ \frac{k}{m}x =0
\end{eqnarray*}
特性根を$\lambda$,任意定数を$X$として,$x$を次のように置く.
\begin{eqnarray*}
x=Xe^{\lambda t}
\end{eqnarray*}
代入して整理すると
\begin{eqnarray*}
\left(\lambda^2+ \frac{k}{m}\right)Xe^{\lambda t} =0
\end{eqnarray*}
よって,次の特性方程式が求められる.
\begin{eqnarray*}
\lambda^2+ \frac{k}{m} =0
\end{eqnarray*}
虚数単位を$i$として,この方程式を解くと次の(2個の)特性根が定まる.
\begin{eqnarray*}
\lambda =\pm i\sqrt{\frac{k}{m}}
\end{eqnarray*}
即ち,この場合の特性は,両符号を持つ純虚数となる.
\begin{eqnarray*}
p=\sqrt{\frac{k}{m}}
\end{eqnarray*}
と置くと,$\pm ip$が特性となるので,$x$の一般解は次式のように置くことができる.
\begin{eqnarray*}
x=X_1e^{ipt}+X_2e^{-ipt}
\end{eqnarray*}
変形すると次のようになる.
\begin{eqnarray*}
x&=&X_1\left(\cos pt+i\sin pt\right)+X_2\left(\cos pt -i\sin pt\right)\\
&=& \left(X1+X2\right)\cos pt + i\left(X_1-X_2\right)\sin pt \\
&\equiv& a_1\cos pt + b_1\sin pt
\end{eqnarray*}
この解は,角振動数$p=\sqrt{\frac{k}{m}}$で振動する正弦波と余弦波の重ね合わせとなる時間の関数であり,コサインでまとめると
\begin{eqnarray*}
&& x=\sqrt{a_1^2+b_1^2}\cos\left(pt -\phi\right) \\
&& \phi=\tan^{-1}\frac{b_1}{a_1}
\end{eqnarray*}
サインでまとめると
\begin{eqnarray*}
&& x=\sqrt{a_1^2+b_1^2}\sin\left(pt + \beta\right) \\
&& \beta=\tan^{-1}\frac{a_1}{b_1}
\end{eqnarray*}
のように,角振動数$p$に対して,振幅と位相が定まるような解となる.ここで,$p$は,モデルの特性(パラメータ)である質量$m$とばね定数$k$で決まる角振動数であることから,固有角振動数と呼ばれる.固有角振動数は,固有振動数や固有周期として,表わすこともできる.この解の物理的な意味としては,ばね定数$k$のばねで支持された質量$m$の物体は,この固有角振動数$p$で振動するような応答をする,ということになる.また,この場合外部から力を受けて振動しているわけでなく,自分自身が(自由に,勝手に)振動していることから,”自由振動”と呼ばれる.そのため,固有振動数は,自由振動数と呼ばれることもある.
振幅と位相,あるいは,未定係数$a_1$,$b_1$は初期条件で定めることができ,例えば,$t=0$において,$x=x_0$,$\dot{x}=v_0$として,未定係数$a_1$,$b_1$を定めることにすると,次の2式を$a_1$,$b_1$の2元1次の連立方程式として解けばよい.ここで,
\begin{eqnarray*}
\dot{x}=p\left(-a_1\sin pt + b_1\cos pt\right)
\end{eqnarray*}
より,
\begin{eqnarray*}
&& x_0=a_1\cos(0)+b_1\sin(0)=a_1 \\
&& v_0=p\left\{-a_1\sin(0) + b_1\cos(0)\right\}=pb_1
\end{eqnarray*}
よって,$t=0$で変位$x=x_0$,速度$\dot{x}=v_0$を与えるとこの系の変位は
\begin{eqnarray*}
x = x_0\cos pt + \frac{v_0}{p}\sin pt
\end{eqnarray*}
のように時間的に変化することが分かる.この解は,初期条件に対する自由振動応答解と言われ,質量を持つ物体が弾性的に支持されている,あるいは,ばねで表現できるような弾性的な変形をする場合には,この解が示すような時間的な変動(応答)をすることになる.
5.4 演習
(1) 図5-11に示すように,東京丸の内から地面に穴を掘り,大阪梅田まで一直線のトンネルをつくる.長さはちょうど500kmとし,摩擦や抵抗を無視して,列車が重力だけによってこの距離を走るのに要する時間と最大速度を求めよ.ただし,地球の周囲は4万kmである.
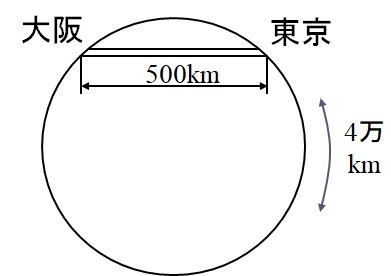
図5-11 重力による東京‐大阪間の列車の振動挙動
(2) 質量$m$がばね定数$k$のばねで鉛直に支持されている.質量$M$を$m$上$h$の高さから$m$に落下させ$m$に打ち当てる.衝突$後$Mと$m$は一体となって運動するものとして$m$の運動を解析せよ.












