6.減衰のない場合の1自由度系の自由振動II
6.1 剛体振子(物理振子)の運動
人間やヒト型ロボットの肩を中心とした上腕の運動や膝を中心とした歩行動作は支点回りの剛体の回転運動と捉えることができ,このモデルは一般に”剛体振子”,あるいは,”物理振子”と呼ばれる.エンジンのピストンクラン機構を担う連接棒(コネクティングロッド)など様座な機械システムの動的な機構部分には”剛体振子”でモデル化できるものが数多く存在する.剛体モデルは,図6-1に示すように鉛直下向きの軸を基準として,反時計回りの支点O回りの回転角度を$\theta$とする.
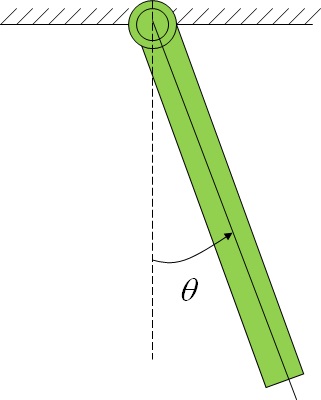
図6-1 剛体モデル
それではこのモデル化に辺り
【QUIZ 1】剛体振子の運動を考えるのに必要な量(物理的パラメータ)として何を考えたらよいであろうか?
剛体回転運動を考える必要があるので,その際に必要となる物体の”慣性”に関わるパラメータと”力の作用点”といった
質量 :$m$
支点O回りの慣性モーメント:$I_O$
支点Oと重心Gの距離 :$l_G$
などである.これらのパラメータを持つ剛体振り子に対して,図6-2に示すように鉛直下向きに$x$軸,水平方向を$y$軸を考える,ここで,支点部に発生する力を$x$軸,$y$軸方向に分解した場合と$r$方向と$\theta$方向に分解した表示を示している.
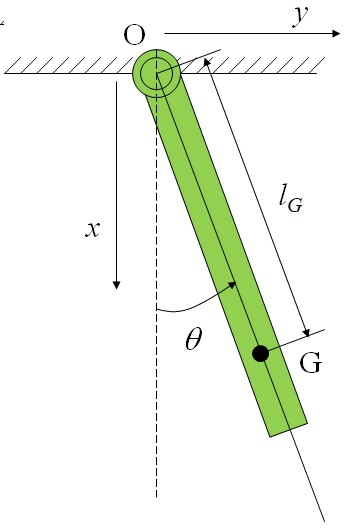
図6-2 剛体モデルの運動
この系に対してFree-body Diagramを考えると図6-3のようになる.一般的な剛体の運動を考える場合は,重心の並進運動と重心回りの回転運動を考えるのが良い.しかしながら,支点を有する回転運動の場合には,支点回りの回転運動を考える方が運動方程式の導出は容易になる.即ち,この場合の支点O回りの回転運動を考えると次のようになる.
\begin{eqnarray*}
I_O\ddot{\theta} = -l_G\times mg\sin\theta
\end{eqnarray*}
$\theta\ll 1$とすると
\begin{eqnarray*}
&& I_O\ddot{\theta} + mgl_G\theta = 0 \\
&& \therefore \ddot{\theta} + \frac{mgl_G}{I_O}\theta = 0
\end{eqnarray*}
よって,固有振動数$f_n$は
\begin{eqnarray*}
f_n = \frac{1}{2\pi}\sqrt{\frac{mgl_G}{I_O}}
\end{eqnarray*}
であり,固有周期$T$は
\begin{eqnarray*}
T = 2\pi\sqrt{\frac{I_O}{mgl_G}}
\end{eqnarray*}
となる.
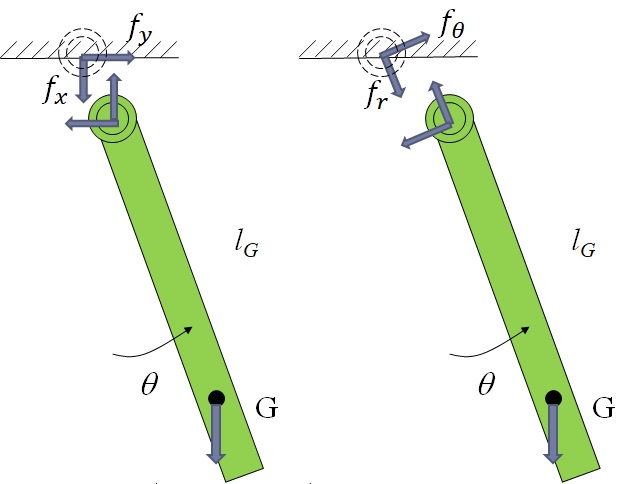
図6-3 剛体モデルのFree-body Diagram
【参考】
いわゆる剛体運動として,運動方程式を求める場合には
$(x,y)$座標系では,加速度ベクトル$\mathbf{a}=\left(\ddot{x},\ddot{y}\right)$に対応する,力ベクトルは
\begin{eqnarray*}
\mathbf{f}=\left(mg-f_x,-fy\right)
\end{eqnarray*}
で表現され,重心回りのモーメントは,
\begin{eqnarray*}
M=-l_G\sin\theta\times f_x + l_G\cos\theta\times f_y
\end{eqnarray*}
により,角速度$\ddot{\theta}$が生じる系と見なすことができる.
一方,$(r,\theta)$座標系では,加速度ベクトル$\mathbf{a}=\left(-l_G\dot{\theta}^2,l_G\ddot{\theta}\right)$に対して,力ベクトルは,
\begin{eqnarray*}
\mathbf{f}=\left(mg\cos\theta-f_r,-mg\sin\theta-f_\theta\right)
\end{eqnarray*}
であり,重心回りのモーメントは,
\begin{eqnarray*}
M=l_G\times f_\theta
\end{eqnarray*}
となる.
【QUIZ 2】剛体振子の慣性モーメントの測定方法について説明せよ.
”自由振動の周期$T$を測定することにより,支点回りの慣性モーメントを測定することができる”
\begin{eqnarray*}
T = 2\pi\sqrt{\frac{I_O}{mgl_G}}
\end{eqnarray*}
の関係を使う.即ち,
\begin{eqnarray*}
I_O = mgl_G\left(\frac{T}{2\pi}\right)^2
\end{eqnarray*}
様々な構造を有する機械構造体に対して,物体の持つ”様々な軸回りの慣性モーメント”の測定する方法として,このような固有周期がよく用いられる.
6.2 傾斜単振子の振動
角度のついた振り子の振動するために,図6-4に示す傾斜単振子を考える.即ち,長さ$l$,質量$m$の単振子が支点から距離$r$の位置をばねで支持され,水平面から$\alpha$だけ傾いた状態で静止している系を考える.知面内における本系の自由振動を解析し,固有角振動数を求める.
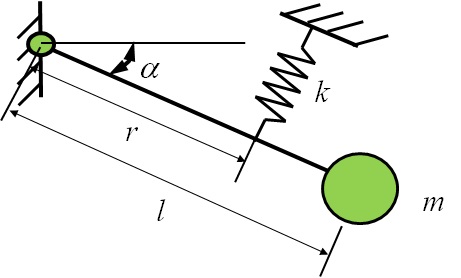
図6-4 傾斜単振子の振動
Free-body Diagramは図6-5のようになる.ばねの自然長からの伸びを$x_0$として,静的な状態における支点回りのモーメントの釣合いを考えると
\begin{eqnarray*}
l\times mg\cos\alpha - krx_0 = 0
\end{eqnarray*}
この位置を原点として図のように微小回転$\theta$を考えると,ばねの伸びは,$x_0+r\theta$となるので,支点回りのモーメントと運動の関係は次のようになる.
\begin{eqnarray*}
ml^2\ddot{\theta} = l\times mg \cos\left(\theta+\alpha\right) - kr\left(x_0+r\theta\right)\cos\theta
\end{eqnarray*}
変形すると
\begin{eqnarray*}
&& ml^2\ddot{\theta} = mgl \cos\theta\cos\alpha - mgl\sin\theta\sin\alpha - kr\left(x_0+r\theta\right)\cos\theta \\
&& \therefore ml^2\ddot{\theta} + mgl\sin\theta\sin\alpha + kr^2\theta\cdot\cos\theta = \cos\theta\left(mgl\cos\alpha-krx_0\right) = 0
\end{eqnarray*}
よって,$\theta\ll 1$より運動方程式は次のようになる.
\begin{eqnarray*}
&& ml^2\ddot{\theta} + \left(kr^2 + mgl\sin\alpha\right)\theta = 0 \\
&& \therefore \ddot{\theta} + \left\{\frac{k}{m}\left(\frac{r}{l}\right)^2 + \frac{g}{l}\sin\alpha\right\}\theta = 0
\end{eqnarray*}
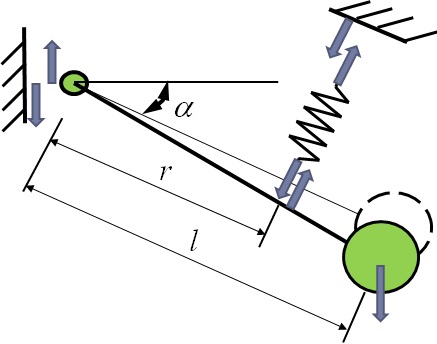
図6-5 傾斜単振子に対するFree-body Diagram
次に自由振動解について考える.定数係数の常微分方程式なので,次の解を仮定できる.
\begin{eqnarray*}
\theta=\Theta e^{\lambda t}
\end{eqnarray*}
運動方程式に代入し整理すると,特性方程式は次のようになる.
\begin{eqnarray*}
\lambda^2 + \left\{\frac{k}{m}\left(\frac{r}{l}\right)^2 + \frac{g}{l}\sin\alpha\right\} = 0
\end{eqnarray*}
よって,
\begin{eqnarray*}
\lambda^2 = - \left\{\frac{k}{m}\left(\frac{r}{l}\right)^2 + \frac{g}{l}\sin\alpha\right\} = 0
\end{eqnarray*}
となるので,$\frac{k}{m}\left(\frac{r}{l}\right)^2 + \frac{g}{l}\sin\alpha \geq 0$のとき,
\begin{eqnarray*}
\lambda = \pm i\sqrt{\frac{k}{m}\left(\frac{r}{l}\right)^2 + \frac{g}{l}\sin\alpha} = \pm ip
\end{eqnarray*}
$i$を虚数単位としており,$p$が固有角振動数となる.また,固有振動数$f_n$を示すと以下のようになる.
\begin{eqnarray*}
f_n = \frac{1}{2\pi}p = \frac{1}{2\pi}\sqrt{\frac{k}{m}\left(\frac{r}{l}\right)^2 + \frac{g}{l}\sin\alpha}
\end{eqnarray*}
この特性根に対する一般解は
\begin{eqnarray*}
\theta = \Theta_1e^{ipt} + \Theta_2e^{-ipt} = \left(\Theta_1+\Theta_2\right)\cos pt + i\left(\Theta_1-\Theta_2\right)\sin pt
\end{eqnarray*}
となるので,$t=0$で$\theta=\theta_0$,$\dot{\theta}=\omega_0$とするとその時の自由振動応答は次式となる.
\begin{eqnarray*}
\theta = \theta_0\cos pt + \frac{\omega_0}{p}\sin pt
\end{eqnarray*}
一方,$\frac{k}{m}\left(\frac{r}{l}\right)^2 + \frac{g}{l}\sin\alpha \leq 0$のとき,
\begin{eqnarray*}
\beta = \sqrt{-\left\{\frac{k}{m}\left(\frac{r}{l}\right)^2 + \frac{g}{l}\sin\alpha\right\}}
\end{eqnarray*}
と置くと,特性根は,$\lambda=\pm\beta$となるので,一般解は
\begin{eqnarray*}
\theta = \Theta_1e^{\beta t} + \Theta_2e^{-\beta t}
\end{eqnarray*}
となるので,$t=0$で$\theta=\theta_0$,$\dot{\theta}=\omega_0$とするとその時の自由振動応答は次式となる.
\begin{eqnarray*}
\theta = \frac{\theta_0+\frac{\omega_0}{\beta}}{2}e^{\beta t} + \frac{\omega_0-\frac{\omega_0}{\beta}}{2}e^{-\beta t}
\end{eqnarray*}
即ち,第一項は,$t\rightarrow\infty$で$e^{\beta t}\rightarrow\infty$となり,発散することを示す解となる.従ってこの場合は,”不安定な系”となる.また,
\begin{eqnarray*}
0\leq\alpha \pi
\end{eqnarray*}
では,
\begin{eqnarray*}
\sin\alpha\geq\pi
\end{eqnarray*}
より,系は”安定”であり,
\begin{eqnarray*}
\alpha =0
\end{eqnarray*}
のとき,固有(角)振動数は重力に無関係となる.また,
\begin{eqnarray*}
\alpha = -\frac{\pi}{2}
\end{eqnarray*}
のとき,”倒立振子”となり,
\begin{eqnarray*}
\frac{g}{l} \geq \frac{k}{m}\left(\frac{r}{l}\right)^2
\end{eqnarray*}
なら,”不安定な系”となる.
6.3 等価ばね,等価質量
並進運動,回転運動どちらにせよ,1自由度振動系の運動方程式が定まれば系の固有振動数を定めることができる.また,大雑把ではあるが1自由度系を仮定した場合の自由振動応答を調べることができる.そのため,様々な機械構造体に対して,1自由度系のモデルパラメータである,質量の大きさとばね定数の大きさを定め,1自由度振動系として調べることがよく行われる.例えば,機械構造物でよくみられる梁構造におけるばね定数について考えてみる.
【QUIZ 3】片持ち梁の撓み曲線を式で示せ.
梁の撓み曲線をの式を使って,最大変位の位置に質量が集中したと仮定した質量$m$,ばね定数$k$に対応する等価的な値を定めることができる.梁で定義される長さ$l$,断面積$A$,断面二次モーメント$I$,及び,密度$\rho$,ヤング率$E$とすると,片持ち梁に対する等価ばね定数$k_e$は
\begin{eqnarray*}
k_e=\frac{3EI}{l^2}
\end{eqnarray*}
また,等価質量$m_e$は,
\begin{eqnarray*}
m_e=\frac{33}{140}\rho Al
\end{eqnarray*}
のように定まる.
6.4 演習
1.直径50cmで一様な厚さの重い円板に,直径10cmの穴があいており,その中心は,円板の中心から15cmはずれている.円板がその中心軸を通る水平軸のまわりに,自由に摩擦なく回転できるように支持されているときの微小振動の周期を求めよ.
2.図6-6は,質量$m=2$kg,AB間の距離$l=0.3$mの連節棒を表しており,点Aから重心Gまでの距離$l_g=0.2$ mの剛体振子(物理振子)と考えることができる.点Aを支点として振子運動をさせ,周期を測ったところ周期 $T=1$ 秒であった.
(1) この剛体振子の重心回りの慣性モーメント$I_G$ を求めよ.
(2) Bの位置を支点として振子運動をさせた場合の固有周期を求めよ.
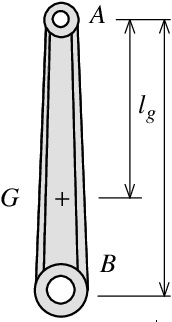
図6-6 剛体振子の慣性モーメントの測定






