�W�D���K���T
8.1�@�U���U���C�����x�C������
8.1.1 $t=0$�ɂ����āC���̂R�ʂ�̏����ŐU�����Ă���ꍇ���l����D
(a) $x=0$�C$\dot{x}=v_0$�̏ꍇ
(b) $x=x_0$�C$\dot{x}=0$�̏ꍇ
(c) $x=x_0$�C$\dot{x}=v_0$�̏ꍇ
���̎��̊p�U������$\omega$�Ƃ��āC(a)�`(c)�ɑ���U�������Ŏ����C����$t$�ɑ���ϓ��̗l�q��}������D
8.1.2 �ԗ��̐U���̐U�������x��0.1g�C�U������2Hz�Ƃ���D�g�`�͐����g�Ɖ��肷��Ƃ��̐U���͉�mm���H
8.1.3 �Q���ݎԂ������㉺�U�������Ă���D�U��20mm�C�U����3Hz�C�ˏ�̎ԑ̎���10t�C�ˉ��̗֎����̑��̎���2t�̂Ƃ��C�ԗւ��烌�[���\�ʂɗ^������͂̍ő�l�͂����炩�H
8.1.4 �}8-1-1�Ɏ����悤�ɁC����$M=20t$�̋@�B�̊�b���C�U��$250\mu m$�C�U����$9$Hz�ŏ㉺�����ɐU�����Ă���D���̋@�B�Ɗ�b�̊ԁi$M$��$M'$�Ƃ̊ԁj�ɂ͂��炭�͂̕ϓ��U���͂����炩�H
�@
�@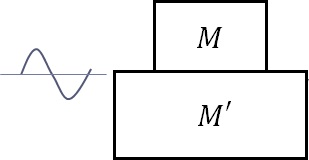
�@�}8-1-1�@��b��ɒu���ꂽ�@�B�̐U��
�@
8.1.5 �U����̏�ɕ��̂��ڂ��C�U�����$60$Hz�̐U����^����D�U����̐U����$0$���炵�����ɑ傫�����Ă������Ƃ��C���̂����ǂ�n�߂�i���Ȃ킿�C���̂��U���䂩�̕\�ʂ��痣��Ĕ�яオ��n�߂�j�U���͉�mm���H
8.2 �P���R�x�n�̎��R�U���T
8.2.1 �˂̉��[�ɏd��$W$�̕��̂��邵�C�Î~�����ʒu����}�ɉ����ɑ��x$v_0$�̏�����^�����Ƃ��C�U��$S$�����������Ă��ǂ����Ƃ����D���̂˂̂˒萔�͂����炩�H
8.2.2 �n���i���a$R$�j�̕\�ʂ���C���S��ʂ��Ĕ��Α��̕\�ʂ܂Ō����@�����Ƃ���D�d�͂̉����x�́C�n���\�ʂł�$g_0$�ł��邪�C���̂Ȃ��ł͒n�����S����̋����ɔ�Ⴗ��Ɖ��肷��ƁC������畨�𗎂Ƃ����Ƃ��C���̔��Α��ɓ��B����܂ł̎��Ԃ���эő呬�x�����߂�D�������C��C��R�͍l���Ȃ����̂Ƃ���D
8.2.3 �}8-2-1�Ɏ����悤�ɁC�ݎ�$20$t�̎ԗ���$40$t�̎ԗ��Ƃ��C�˒萔$1$kN/mm�̘A����ŘA������Ă���D�����̎Ԃ����Ή^������Ƃ��̌ŗL�U���������߂�D�������C�ԗւ̓]���薀�C�⊵�����[�����g�Ȃǂ͖����ł���Ƃ���D
�@
�@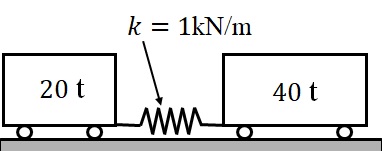
�@�}8-2-1�@�Q�̎ԗ��̑��ΐU��
�@
8.3 �P���R�x�n�̎��R�U���U
8.3.1 �}8-3-1�Ɏ����|���U�q�̌ŗL�U������Hz���ŕ\�킷���œ����D�������C�˂Ǝ��ʂ����ԃ��o�[���ނ̎��ʂ͖������Ă悢�D
�@
�@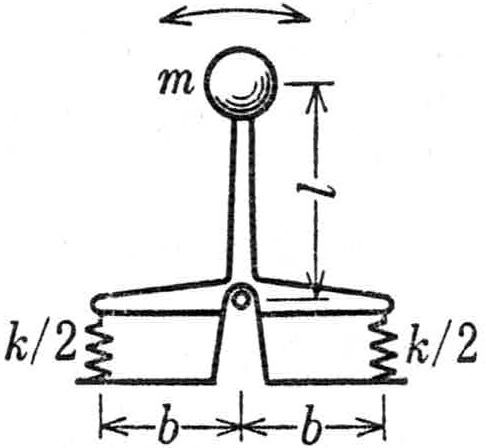
�@�}8-3-1�@�|���U�q�̐U��
�@
8.3.2 �}8-3-2�̌n�̌ŗL�U���������߂�D�������C�_�̒f�ʂ͒����ɉ����Ĉ�l�ŁC�_�̎��ʂ�$10$kg�ł���D�˂P�̂˒萔��$40$N/cm�Ƃ���D�ˎ��t���̂��߂ɖ_����o�Ă���r�̎��ʂ͖������Ă悢�D
�@
�@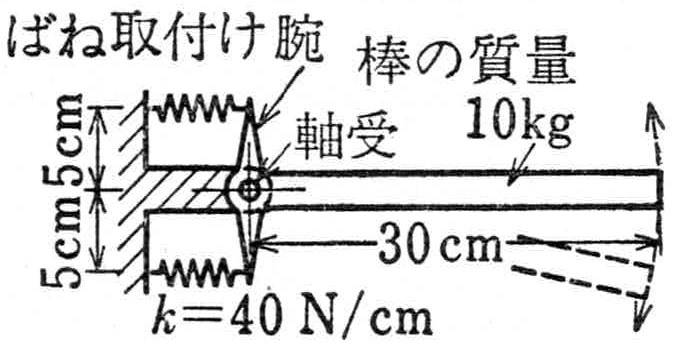
�@�}8-3-2�@���̐U�q�̐U��
�@
8.4 �P���R�x�n�̎��R�U���V
8.4.1 �}8-4-1�Ɏ��������U�q������D�n�̌������40%�ɂ��邽�߂ɁC�_���p�ɗ^����ׂ������W���̒l�����߂�D�������C�U�q�̎��ʂ�$300$kg�C�d�S���̉�]���a��$50$cm�Ƃ���D
�@
�@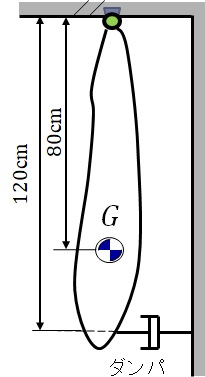
�@�}8-4-1�@�����U�q�̐U��
�@
8.4.2 �}8-4-2�Ɏ�����]�U���n�̌�����C�ΐ��������C�����ŗL�U���������߂�D�������C$m=20$kg�C$l=0.6$m�C$a=0.3$m�C$b=0.4$m�C$k=8000$N/m�C$c=200$N$\cdot$s/m�ł���D
�@
�@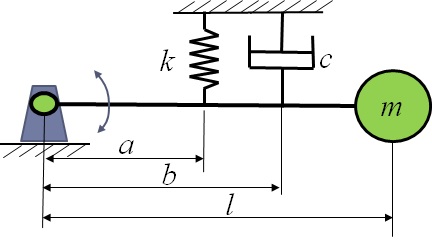
�@�}8-4-2�@��]�U���n�̐U��
�@






