9.減衰のない場合の1自由度系の強制振動
9.1 振動現象の種類・分類
これまで,機械システムに発生する振動を1自由度系でモデル化して,”自由振動”について調べてきた.この振動は,最初に初期変位,あるいは,初期速度が与えられた後に起こる振動であり,振動中に外部から力が作用しているわけではない.しかしながら,振動工学ハンドブック(養賢堂発行)には,
・自由振動 (free vibration):励振を取り除いた後に起こる振動
と記載されており,実際問題では,振動を誘発する”励振”が振動が発生する以前に作用していたと考えるのが一般的であると思われる.つまり,”自由振動”が発生する以前に何らかの力が作用しており,その結果として初期条件となる初期変位や初期速度が与えられて”自由振動”が発生するというのが実際に起こり得る現象である.機械システムを運転するためには,何らかの入力が必要である.起動時に加えた力は,結果として”自由振動”を誘発する可能性がある.また,運転状態を継続するためには,外部から力を加え続ける必要があるが,その力は機械システムに運動を伴う何らかの変形を誘発する可能性があり,それは振動現象として現れる.運転開始時,あるいは,運転中に振動が発生した場合は,単なる”自由振動”ではなく,運転に関連する何らかの”励振力”が作用した結果として起こる振動と捉えるべきであり,それは自由に振動している”自由振動”のみでは現象を説明できない.機械システムの運動は,繰り返し動作が多く,周期性を持つことから,周期的な入力を励振力とするのが常である.ここでは,振動工学ハンドブックに,
・強制振動(forced vibration) : 周期的な励振によって発生する定常振動
と記載されている振動現象を調べることにする.この振動現象は,”自由振動”に現れる”過渡的な振動”に対比して,”定常振動”と捉えられるが,”自由振動”で現れる特徴を反映した現象を調べることができ,機械システムの設計指針や運転指針の基礎となるものである.同ハンドブックには”自由振動”,”強制振動”の他に,
・(機械)振動(vibration) : 機械系の運動又は変位を表す量の大きさが、ある平均値又は基準値よりも大きい状態と小さい状態を交互に繰り返す時間的な変化.
・周期振動(periodic vibration) : 独立変数がある一定値増加するごとに、同じ値を繰り返すような関数によって示される振動.
$\star$時間の関数として示される周期量$y$は、次のように表される.
\begin{eqnarray*}
y=f(t)=f(t+nT)
\end{eqnarray*}
ここで、$n$;整数,$T$:定数,$t$: 独立変数.
・不規則振動(random vibration) : 任意の時刻における大きさが正確に予知できない振動.
・定常振動(steady-state vibration) : 継続的な周期振動.
・過度振動(transient vibration) : 定常状態でない振動.
などが記載されている.これらは,現実に起こる様々な”振動現象”の特徴を表しているが,実際の振動がこれらのどれかに分類されるわけではなく,起こっている振動は,これらの特徴のいくつかを有していると考えるべきである.
9.2 強制振動
図9-1に示すように,質量$m$,ばね定数$k$の不減衰の1自由度系に$f(t)=P\cos\omega t$の周期的な励振力が作用している系を考える.
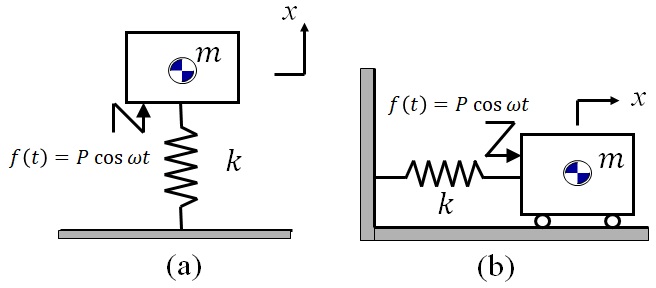
図9-1 1自由度不減衰系の強制振動
この系に対するFree-body Diagramは図8-2のようになる.図に示す力は
\begin{eqnarray*}
&& f_k = kx \\
&& f(t)=P\cos\omega t
\end{eqnarray*}
であるので,運動方程式は次のようになる.
\begin{eqnarray*}
m\ddot{x} = f(t) - f_k = P\cos\omega t - kx
\end{eqnarray*}
\begin{eqnarray*}
\therefore m\ddot{x} + kx = P\cos\omega t
\end{eqnarray*}
両辺を$m$で割ると
\begin{eqnarray*}
\ddot{x} + \frac{k}{m}x = \frac{P}{m}\cos\omega t
\end{eqnarray*}
この方程式は,非同次の常微分方程式となるので,解は,右辺を零とおいて得られる同次解と右辺を成り立たせる解(特解)との和となる.
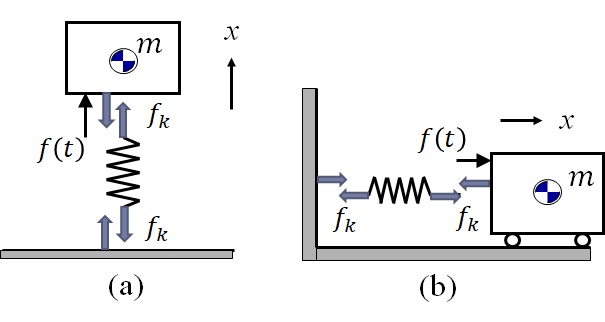
図9-2 1自由度不減衰系強制振動に対するFree-body Diagram
同次解$x_h$はすでに導出しており,この系の固有角振動数$p=\sqrt{\frac{k}{m}}$と未定係数$a_1$,$b_1$を用いて次のようになる.
\begin{eqnarray*}
x_h = a_1\cos pt + b_1\sin pt
\end{eqnarray*}
一方特解$x_s$は,左辺において必要な微分を施した際に現れる関数形を仮定すればよいので,微分して$\cos\omega t$が現れるのは,$\cos\omega t$もしくは$\sin\omega t$なので,未定係数を$a_2$,$b_2$として,次のように仮定することができる.
\begin{eqnarray*}
x_s = a_2\cos\omega t + b_2\sin\omega t
\end{eqnarray*}
特解$x_s$で表した運動方程式
\begin{eqnarray*}
\ddot{x}_s + p^2x_s = \frac{P}{m}\cos\omega t
\end{eqnarray*}
に代入すると次式を得る.
\begin{eqnarray*}
\left(p^2a_2-a_2\omega^2 -\frac{P}{m}\right)\cos\omega t + b_2\sin\omega t = 0
\end{eqnarray*}
よって,未定係数は次のようになる.
\begin{eqnarray*}
&& a_2=\frac{P/m}{p^2-\omega^2} \\
&& b_2 =0
\end{eqnarray*}
ここで,
\begin{eqnarray*}
\frac{P}{m}=\frac{P}{m}=\frac{P}{k}\frac{k}{m}=\frac{P}{k}p^2
\end{eqnarray*}
より,$\delta_{st}=P/k$とおくと,特解は次のようになる.
\begin{eqnarray*}
x_s = \frac{\delta_{st}p^2}{p^2-\omega^2}\cos\omega t = \frac{\delta_{st}}{1-\left(\frac{\omega}{p}\right)^2}\cos\omega t
\end{eqnarray*}
従って,この系の応答は次式となる.
\begin{eqnarray*}
x=x_h + x_s = a_1\cos pt+ b_1\sin pt + \frac{\delta_{st}}{1-\left(\frac{\omega}{p}\right)^2}\cos\omega t
\end{eqnarray*}
時間微分して速度を求めると次式となる.
\begin{eqnarray*}
\dot{x} = p\left(-a_1\sin pt+ b_1\cos pt\right) - \frac{\omega\delta_{st}}{1-\left(\frac{\omega}{p}\right)^2}\sin\omega t
\end{eqnarray*}
よって,初期条件を$t=0$において,$x=x_0$,$\dot{x}=v_0$とすると次式を得る.
\begin{eqnarray*}
&& x_0 = a_1 + \frac{\delta_{st}}{1-\left(\frac{\omega}{p}\right)^2}\\
&& v_0 = pb_1
\end{eqnarray*}
故に,
\begin{eqnarray*}
\left.\begin{array}{l}
a_1 = x_0 -\frac{\delta_{st}}{1-\left(\frac{\omega}{p}\right)^2}\\
b_1 = \frac{v_0}{p}
\end{array}\right\}
\end{eqnarray*}
即ち,この系の応答は次式となる.
\begin{eqnarray*}
x = \left\{x_0 -\frac{\delta_{st}}{1-\left(\frac{\omega}{p}\right)^2}\right\}\cos pt + \frac{v_0}{p}\sin pt + \frac{\delta_{st}}{1-\left(\frac{\omega}{p}\right)^2}\cos\omega t
\end{eqnarray*}
この式から,この系の応答は,系の固有角振動数$p=\frac{k}{m}$で振動する自由振動応答に対応する項と励振力の角周波数(角振動数)$\omega$で応答する項の和で表現されることが分かる.ここで,
\begin{eqnarray*}
x_0 =\frac{\delta_{st}}{1-\left(\frac{\omega}{p}\right)^2}\text{, }v_0 = 0
\end{eqnarray*}
のとき,
\begin{eqnarray*}
x = \frac{\delta_{st}}{1-\left(\frac{\omega}{p}\right)^2}\cos\omega t
\end{eqnarray*}
となる.この解は,励振力の角振動数で応答する場合を示しており,この時の応答は,強制振動応答と呼ばれる.即ち,系の強制振動応答では,自由振動応答の項を含まない,励振力により強制的に発生させられる応答のみを考える.
一方,$\omega\approx p$を考えるために,
\begin{eqnarray*}
&& p-\omega = 2\Delta \\
&& p+\omega \approx 2\omega
\end{eqnarray*}
とすると
\begin{eqnarray*}
&& \cos pt = \cos\left(\frac{p+\omega+p-\omega}{2}\right)t = \cos\omega t\cos\Delta t - \sin\omega t\sin\Delta t \\
&& \sin pt = \sin\left(\frac{p+\omega+p-\omega}{2}\right)t = \sin\omega t\cos\Delta t + \cos\omega t\sin\Delta t
\end{eqnarray*}
また,
\begin{eqnarray*}
&& \frac{1}{1-\left(\frac{\omega}{p}\right)^2} = \frac{p^2}{(p^2-\omega^2}\approx\frac{\omega^2}{\left(p-\omega\right)\left(p+\omega\right)} = \frac{\omega^2}{2\Delta\cdot2\omega}=\frac{\omega}{4\Delta} \\
&& \cos\omega t\approx \cos pt = \cos\omega t\cos\Delta t - \sin\omega t\sin\Delta t
\end{eqnarray*}
となるので,応答は次のようになる.
\begin{eqnarray*}
x &=& \left\{x_0 -\frac{\omega\delta_{st}}{4\Delta}\right\}\left(\cos\omega t\cos\Delta t - \sin\omega t\sin\Delta t\right) + \frac{v_0}{p}\left(\sin\omega t\cos\Delta t + \cos\omega t\sin\Delta t \right) + \frac{\omega\delta_{st}}{4\Delta}\left(\cos\omega t\cos\Delta t - \sin\omega t\sin\Delta t\right) \\
&=& \left\{\left(x_0 -\frac{\omega\delta_{st}}{4\Delta}\right)\cos\Delta t + \frac{v_0}{p}\sin\Delta t + \frac{\omega\delta_{st}}{4\Delta}\cos\Delta t\right\}\cos\omega t
+ \left\{\left(-x_0 + \frac{\omega\delta_{st}}{4\Delta}\right)\sin\Delta t + \frac{v_0}{p}\cos\Delta t + \frac{\omega\delta_{st}}{4\Delta}\sin\Delta t\right\}\sin\omega t
\end{eqnarray*}
よって,$\Delta \ll 1$のとき,
\begin{eqnarray*}
x &\approx& \left(x_0 + \frac{v_0}{p}\Delta t\right)\cos\omega t + \left\{-\left(x_0 + \frac{\omega\delta_{st}}{2\Delta}\right)\Delta t + \frac{v_0}{p}\right\}\sin\omega t \\
&=&\left(x_0 + \frac{v_0}{p}\Delta t\right)\cos\omega t + \left(-x_0 + \frac{v_0}{p} + \frac{\omega\delta_{st}}{2}t\right)\sin\omega t
\end{eqnarray*}
よって,第3項
\begin{eqnarray*}
\frac{\omega\delta_{st}}{2}t\sin\omega t
\end{eqnarray*}
は,$\omega\approx p$のとき,振幅が時間と共に増大することを示しており,時間的変動は励振力の$\cos\omega t$ではなく,$\sin\omega t$で変動することが分かる.つまり,$\omega$の値を徐々に変化させ,$p$の値に近づいていくと,この振幅が時間と共に増大することになるが,最初余弦振動であったものが正弦振動に変化するということが起こる.強制振動応答
\begin{eqnarray*}
x = \frac{\delta_{st}}{1-\left(\frac{\omega}{p}\right)^2}\cos\omega t
\end{eqnarray*}
の応答振幅$A$は
\begin{eqnarray*}
A = \frac{\delta_{st}}{1-\left(\frac{\omega}{p}\right)^2}
\end{eqnarray*}
であり,この応答振幅$A$は"励振角周波数$\omega$の関数"と見なすことができる.横軸に無次元化角周波数$\frac{\omega}{p}$,縦軸に無次元化振幅$\frac{A}{\delta_{st}}$を取り,グラフに表わすと,図9-3のようになる.
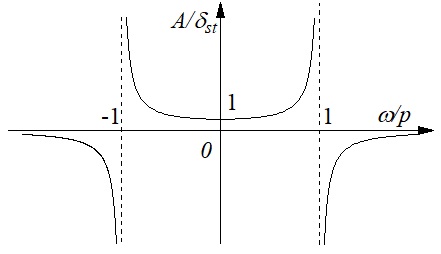
図9-3 1自由度不減衰系の周波数応答曲線
図から明らかなように$\omega$の絶対値を零から徐々に大きくしていくと,振動振幅は次第に大きくなり,$\frac{\omega}{p}=\pm1$のとき,振動振幅は最大(この場合は無限大)となる.この時の状態を”共振(resonance)”あるいは,共振状態という.この値を越えると,振動振幅はマイナス無限だとなり,更に周波数を大きくすると符号が負の振幅のまま,大きさは次第に小さくなり,零に近づいていく様子が分かる.ここで,$\frac{\omega}{p}\pm1$,即ち,$\omega\pm p$の前後で振幅の符号が変化する.
Quiz 1 これは何を意味すると考えたらよいであろうか?
$\omega\approx p$で考えると余弦的な変動が正弦的な変動に変わるということが分かった.これは,振動の基本表現である,振幅,振動数,位相を使って表わすと次のようになる.即ち,
\begin{eqnarray*}
x= A\cos(\omega t - \varphi)
\end{eqnarray*}
において,$0\leq \omega < p$では,$\varphi=0$であり,$\omega \approx p$のときには,$\varphi=\frac{\pi}{2}$と考えると,
\begin{eqnarray*}
x= A\cos(\omega t - \frac{\pi}{2}) =A\sin\omega t
\end{eqnarray*}
と変形できる.さらに,$\omega\geq p$のときに,$\varphi = \pi$と考えると
\begin{eqnarray*}
x= A\cos(\omega t - \pi) = -A\cos\omega t
\end{eqnarray*}
となり,振幅の符号の変化は,”位相”を使って考えなくても良いことになる.即ち,振幅は大きさのみを考えれば良いので,応答曲線を振幅と位相を使って表わすと図9-4のようになる.
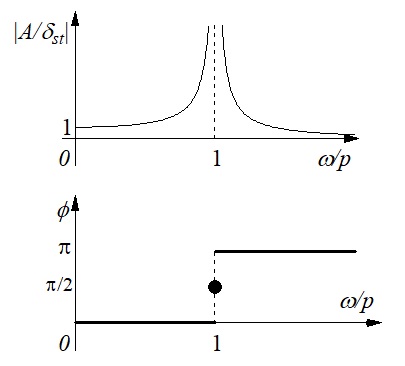
図9-4 1自由度不減衰系の周波数応答の振幅と位相特性
図9-4に示す振幅特性は,機械を運転する際の判定基準として用いられることがある.即ち,運転時の振動振幅基準値が$r$の場合,
\begin{eqnarray*}
\left|A\right| =\frac{\delta_{st}}{\left|1-\left(\frac{\omega}{p}\right)^2\right|}\leq r
\end{eqnarray*}
となるように,$\delta_{st}$,$p$,$\omega$などを検討する.この許容値を越える$\omega$を危険範囲と呼び,それを避ける設計や運転範囲が設定される.また,$\omega\rightarrow p$のとき,$\omega$を危険角周波数のように”危険”何某という言い方をする.
9.3 演習
(1) 周期的な加振力が加わる質量$5$kgの機械をばね定数$2$kN/mの防振ゴムで支持する.加振力の振幅は$10$Nとして,加振周波数が5Hzの時,強制振動の振幅はいくらになるか?また,周波数が3Hzになると振幅はいくらになるか?
(2) 図9-5に示す系の質量$m$の物体に,正弦波状の外力が作用するときの定常応答を計算し,応答の振幅,位相,振動数について説明せよ.ここで,$F_0=10$N,$f_0=5$Hzとする.
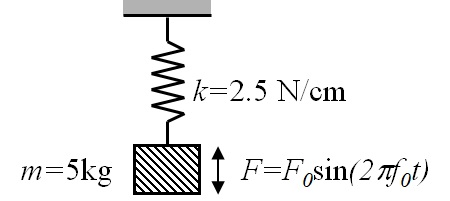
図9-5 1自由度不減衰系の強制振動





