12.振動の測定と制御
12.1 振動計の数学モデル
機械システムに発生する振動現象を1自由度系でモデル化して調べてきたが,実際に起こっていることを調べるには,実際の振動データを取得する必要がある.振動を測定する装置は”振動計”で,振動変位,振動速度,振動加速度などが用途に応じて用いられる.ところで,
Quiz 1:身の回りで振動計が利用されている例を上げよ.
と言われたとき,何を想像するであろうか?
例えば,Smart Phoneにも搭載されており,図12-1に示すように,Wiiリモコンには”モーションセンサー”として3次元的な加速度を測定する”振動計”が搭載されている.図に示す$xyz$方向の加速度を計測することができ,その値をもとにリモコンの動きを推定している.
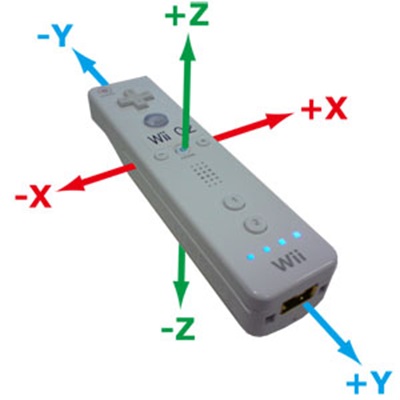
図12-1 Wiiリモコン 加速度センサ(振動計)
(モーションセンサー / 3次元加速度センサー)
振動計の基本的な構造を図12-2に示す.筐体(ケース)のなかに,ばね支持されたおもりが振動系を形成するように設置されており,おもりの振動は圧電体に伝わり”圧電効果”により,振動変位あるいは加速度に比例した電圧(電荷)が出力される.振動している物体に設置することにより,筐体自体の振動により,内部のおもりが振動し,圧電体に電気的な変動が起こるので,それを測定することにより,振動変位などの物理量を測定できる振動計として用いることができる.
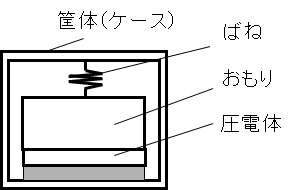
図12-2 振動計の基本的な構造
このセンサーを$u(t)$で表現できる関数で時間的に変動している物体に設置した場合の出力応答について考える.
Quiz 2:振動計を数学モデルで表わすと?
この系は,図12-3に示すように変位励振を受ける1自由度粘性減衰系でモデル化することができる.振動物体の変位を振幅$a$,角周波数$\omega$の正弦波と置くと,$u=a\sin\omega t$となるので,筐体の支持部に基準(原点)を設けた相対変位$x_r$を用いてこの系の運動方程式は次式のようになる.
\begin{eqnarray*}
m\ddot{x}_r + c\dot{x}_r + kx_r = -mu(t) = m\omega^2\sin\omega t
\end{eqnarray*}
よって,定常応答を求めると
\begin{eqnarray*}
x_r =x_r(t) = \frac{a\left(\frac{\omega}{p}\right)^2}{\sqrt{\left\{1-\left(\frac{\omega}{p}\right)^2\right\}^2+\left(2\zeta\frac{\omega}{p}\right)^2}}\sin\left(\omega t - \varphi\right)
\end{eqnarray*}
但し,
\begin{eqnarray*}
\varphi=\tan^{-1}\frac{2\zeta\frac{\omega}{p}}{1-\left(\frac{\omega}{p}\right)^2}\text{, }\quad p=\sqrt{\frac{k}{m}}\text{, }\quad \zeta=\frac{c}{2\sqrt{mk}}
\end{eqnarray*}
ちなみに,絶対系(絶対座標)では,次のような応答となる.
\begin{eqnarray*}
&& x =a\sqrt{\frac{1+ \left(2\zeta\frac{\omega}{p}\right)^2}{\left\{1-\left(\frac{\omega}{p}\right)^2\right\}^2+\left(2\zeta\frac{\omega}{p}\right)^2}}
\sin\left(\omega t-\theta\right) \\
&& \tan\theta = \frac{2\zeta\left(\frac{\omega}{p}\right)^3}{1-\left(\frac{\omega}{p}\right)^2 + \left(2\zeta\frac{\omega}{p}\right)^2}
\end{eqnarray*}
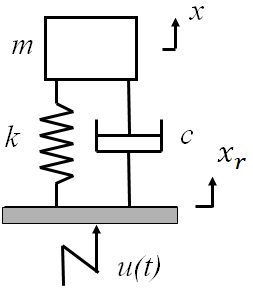
図12-3 振動計の数学モデル
12.2 振動計の設計:モデルバラメータの決定
センサ―の設計に当たっては,モデルパラメータである$m$,$c$,$k$を調整して,性能や用途等を満たすことが求められる.センサーの即応性も必要であるが過渡的な変動はなるべく無くした方が良いので,一般に減衰比は大きい値とする場合が多い.ここでは,
\begin{eqnarray*}
\zeta = \frac{c}{2\sqrt{mk}} = \frac{1}{\sqrt{2}}
\end{eqnarray*}
とする.この時,
\begin{eqnarray*}
&& x_r(t) = \frac{a\left(\frac{\omega}{p}\right)^2}{\sqrt{\left\{1-\left(\frac{\omega}{p}\right)^2\right\}^2+2\left(\frac{\omega}{p}\right)^2}}\sin\left(\omega t - \varphi\right)
= \frac{a\left(\frac{\omega}{p}\right)^2}{\sqrt{1+\left(\frac{\omega}{p}\right)^4}}\sin\left(\omega t-\varphi\right) \\
&& \varphi=\tan^{-1}\frac{\sqrt{2}\frac{\omega}{p}}{1-\left(\frac{\omega}{p}\right)^2}
\end{eqnarray*}
i) $\frac{\omega}{p} \gg 1$となるように,$m$,$k$を設定する.
すると,応答は次式のようになる.
\begin{eqnarray*}
&& x_r(t) = \frac{a\left(\frac{\omega}{p}\right)^2}{\sqrt{1+\left(\frac{\omega}{p}\right)^4}}\sin\left(\omega t-\varphi\right) \fallingdotseq \frac{a\left(\frac{\omega}{p}\right)^2}{\sqrt{\left(\frac{\omega}{p}\right)^4}}\sin\left(\omega t-\varphi\right) = a\sin\left(\omega t-\varphi\right) \\
&& \varphi=\tan^{-1}\frac{\sqrt{2}\frac{\omega}{p}}{1-\left(\frac{\omega}{p}\right)^2} \fallingdotseq \tan^{-1}\frac{\sqrt{2}}{-\frac{\omega}{p}} \fallingdotseq \tan^{-1}(-0) = \pi
\end{eqnarray*}
よって,この場合のセンサー出力は,
\begin{eqnarray*}
x_r(t) = a\sin\left(\omega t-\pi\right) = -a\sin\omega t = -u(t)\\
\end{eqnarray*}
となり,$x_r(t)$は,物体の変位$u(t)$に比例した応答となる.即ち,振動変位計として利用することができる.
振動計の特性$\frac{\omega}{p}\gg 1$は,
\begin{eqnarray*}
\omega \gg p\quad\text{ or }\quad p\ll \omega
\end{eqnarray*}
と表現でき,センサー自体の固有角振動数$p$を測定しようとしている角周波数$\omega$(の帯域)よりも小さく設定することが求められることになる.一般に$\frac{1}{\sqrt{2}}$以下とする.また,$p^2=\frac{k}{m}$の関係から,$m$をある程度大きくするか$k$を小さくすることが必要であり,減衰比は$\zeta=\frac{1}{\sqrt{2}}$程度に設定する場合が多く,一般に$0.5\sim0.7$辺りが用いられる.
ii) $\frac{\omega}{p}\ll 1$の場合
内部のおもりの応答は次式のようになる.
\begin{eqnarray*}
&& x_r(t) = \frac{a\left(\frac{\omega}{p}\right)^2}{\sqrt{1+\left(\frac{\omega}{p}\right)^4}}\sin\left(\omega t-\varphi\right) \fallingdotseq a\left(\frac{\omega}{p}\right)^2\sin\left(\omega t-\varphi\right) \\
&& \varphi=\tan^{-1}\frac{\sqrt{2}\frac{\omega}{p}}{1-\left(\frac{\omega}{p}\right)^2} \fallingdotseq \tan^{-1}\sqrt{2}\frac{\omega}{p} \fallingdotseq 0
\end{eqnarray*}
よって,センサー出力は,次のように表すことができる.
\begin{eqnarray*}
x_r(t) = a\left(\frac{\omega}{p}\right)^2\sin\omega = \frac{1}{p^2}a\omega^2\sin\omega t = -\frac{1}{p^2}\ddot{u}(t)\\
\end{eqnarray*}
即ち,$x_r(t)$は,物体の加速度$\ddot{u}(t)$に比例した応答となる.つまり,加速度計として利用することができる.
特性$\frac{\omega}{p}\ll 1$は,
\begin{eqnarray*}
\omega \ll p\quad\text{ or }\quad p\gg \omega
\end{eqnarray*}
となるので,センサー自体の固有角振動数を測定しようとしている角周波数$\omega$の帯域よりも高い値に設定する必要がある.一般に$\sqrt{2}$倍以上と言われている.固有角振動数$p=\sqrt{\frac{k}{m}}$の値を大きくすれば良いので,$m$を非常に小さくする,あるいは,$k$を大きいものに設定することで実現できる.
12.3 振動によって発生する力とその伝播
図12-4に示すような1自由度粘性減衰系の強制振動において,強制入力による機械自体の応答だけでなく,発生する振動がばねとダッシュポットの支持点を通して外部に伝わっていくことも問題なる.そこで,振動応答に伴う力の伝播特性について調べることにする.この系の運動方程式は次のようになる.
\begin{eqnarray*}
m\ddot{x} + c\dot{x} + kx = P\cos\omega t
\end{eqnarray*}
よって,$p^2=\frac{k}{m}$,$\zeta=\frac{c}{2\sqrt{mk}}$,$\delta_{st}=\frac{P}{k}$とおくと
\begin{eqnarray*}
\ddot{x} + 2\zeta p\dot{x} + p^2x = p^2\delta_{st}\cos\omega t
\end{eqnarray*}
となるので,定常応答を
\begin{eqnarray*}
x = A\cos\omega t + B\sin\omega t
\end{eqnarray*}
として,応答振幅を求める.即ち,運動方程式に代入すると
\begin{eqnarray*}
\left(p^2-\omega^2\right)\left(A\cos\omega t + B\sin\omega t\right) +2\zeta p\omega\left(-A\sin\omega t + B\cos\omega t\right) = p^2\delta_{st}\cos\omega t
\end{eqnarray*}
\begin{eqnarray*}
\therefore \cos\omega t\left\{\left(p^2-\omega^2\right)A + 2\zeta p\omega B -p^2\delta_{st}\right\} +\sin\omega t\left\{\left(p^2-\omega^2\right)B - 2\zeta p\omega A\right\} = 0
\end{eqnarray*}
よって次の行列形式の連立一次方程式を得る.
\begin{eqnarray*}
\left[\begin{array}{cc}
p^2-\omega^2 & 2\zeta p\omega\\
- 2\zeta p\omega & p^2-\omega^2
\end{array}\right]\left[\begin{array}{c}
A \\ B
\end{array}\right]=\left[\begin{array}{c}
p^2\delta_{st} \\ 0
\end{array}\right]
\end{eqnarray*}
\begin{eqnarray*}
\therefore \left[\begin{array}{c}
A \\ B
\end{array}\right]=
\frac{p^2\delta_{st}}{\left(p^2-\omega^2\right)^2 + \left(2\zeta p\omega\right)^2}
\left[\begin{array}{cc}
p^2-\omega^2 & -2\zeta p\omega\\
2\zeta p\omega & p^2-\omega^2
\end{array}\right]\left[\begin{array}{c}
1 \\ 0
\end{array}\right] = \frac{p^2\delta_{st}}{\left(p^2-\omega^2\right)^2 + \left(2\zeta p\omega\right)^2}\left[\begin{array}{c}
p^2-\omega^2 \\ 2\zeta p\omega
\end{array}\right]
\end{eqnarray*}
分母分子を$p^4$で割ると次式となる.
\begin{eqnarray*}
\therefore \left[\begin{array}{c}
A \\ B
\end{array}\right]=\frac{\delta_{st}}{\left\{1-\left(\frac{\omega}{p}\right)^2\right\}^2 + \left(2\zeta \frac{\omega}{p}\right)^2}\left[\begin{array}{c}
1-\left(\frac{\omega}{p}\right)^2 \\ 2\zeta \frac{\omega}{p}
\end{array}\right]
\end{eqnarray*}
よって,物体の変位応答は次式となる.
\begin{eqnarray*}
x&=& \frac{\delta_{st}}{\left\{1-\left(\frac{\omega}{p}\right)^2\right\}^2 + \left(2\zeta \frac{\omega}{p}\right)^2}\left[
\left\{1-\left(\frac{\omega}{p}\right)^2\right\}\cos\omega t + 2\zeta \frac{\omega}{p}\sin\omega t\right] \\
&=& \frac{\delta_{st}}{\sqrt{\left\{1-\left(\frac{\omega}{p}\right)^2\right\}^2 + \left(2\zeta \frac{\omega}{p}\right)^2}}\cos\left(\omega t - \varphi\right) \\
&\quad& \varphi = \tan^{-1}\frac{2\zeta\frac{\omega}{p}}{1-\left(\frac{\omega}{p}\right)^2}
\end{eqnarray*}
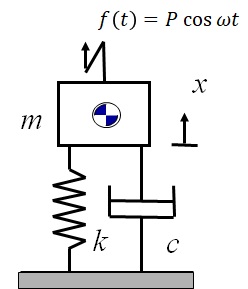
図12-4 1自由度粘性減衰系の強制振動
Quiz 3:物体の振動によって基礎に伝わる力は?
1自由度粘性減衰系の強制振動モデルに対して,Free-body Diagramを描くと図11-5のようになる.即ち,振動によって基礎には図に示す上向きの力$q(t)$が作用する.ここで,
\begin{eqnarray*}
f_k = kx= kx(t) \\
f_c =c\dot{x} = c\dot{x}(t)
\end{eqnarray*}
なので,$q(t)$は次式となる.
\begin{eqnarray*}
q(t) &=& f_k + f_c = kx(t)+ c\dot{x}(t) \\
&=&k\frac{\delta_{st}}{\sqrt{\left\{1-\left(\frac{\omega}{p}\right)^2\right\}^2 + \left(2\zeta \frac{\omega}{p}\right)^2}}\cos\left(\omega t - \varphi\right) -c\omega\frac{\delta_{st}}{\sqrt{\left\{1-\left(\frac{\omega}{p}\right)^2\right\}^2 + \left(2\zeta \frac{\omega}{p}\right)^2}}\sin\left(\omega t - \varphi\right) \\
&=&\frac{P/k}{\sqrt{\left\{1-\left(\frac{\omega}{p}\right)^2\right\}^2 + \left(2\zeta \frac{\omega}{p}\right)^2}}\left\{k\cos\left(\omega t - \varphi\right)-c\omega\sin\left(\omega t - \varphi\right) \right\} \\
&=&\frac{P}{\sqrt{\left\{1-\left(\frac{\omega}{p}\right)^2\right\}^2 + \left(2\zeta \frac{\omega}{p}\right)^2}}\sqrt{1+\left(\frac{c\omega}{k}\right)^2}\cos\left(\omega t - \varphi + \alpha \right)\text{, }\quad \alpha=\tan^{-1}\frac{c\omega}{k}
\end{eqnarray*}
ここで,
\begin{eqnarray*}
\frac{c\omega}{k}=2\frac{c}{2\sqrt{mk}}\frac{\omega}{\sqrt{\frac{k}{m}}}=2\zeta\frac{\omega}{p}
\end{eqnarray*}
より,床に働く力は次式となる.
\begin{eqnarray*}
q(t) =P\sqrt{\frac{1+\left(2\zeta\frac{\omega}{p}\right)^2}{\left\{1-\left(\frac{\omega}{p}\right)^2\right\}^2 + \left(2\zeta \frac{\omega}{p}\right)^2}}
\cos\left(\omega t - \varphi + \alpha \right)\equiv Q\cos\left(\omega t - \varphi + \alpha \right)
\end{eqnarray*}
物体に作用している力の振幅$P$に対して,基礎の作用する力の振幅$Q$は次式のような比率となる.
\begin{eqnarray*}
\frac{Q}{P} = \sqrt{\frac{1+\left(2\zeta\frac{\omega}{p}\right)^2}{\left\{1-\left(\frac{\omega}{p}\right)^2\right\}^2 + \left(2\zeta \frac{\omega}{p}\right)^2}} \equiv \tau
\end{eqnarray*}
ここで,定義される$\tau$は,ばねとダッシュポットで指示された物体に作用している力の大きさが基礎にどの位伝わるかを表わす量で,”力に関する振動伝達率”と呼ばれる.
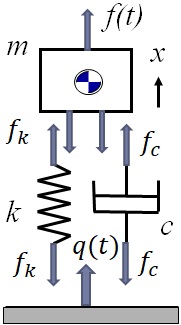
図12-5 1自由度粘性減衰系の強制振動におけるFree-body Diagram
ここで,変位励振受ける系に対して得られた入力変位$u=u(t)a\sin\omega t$に対して得られた物体の絶対変位応答を示すと
\begin{eqnarray*}
x =a\sqrt{\frac{1+ \left(2\zeta\frac{\omega}{p}\right)^2}{\left\{1-\left(\frac{\omega}{p}\right)^2\right\}^2+\left(2\zeta\frac{\omega}{p}\right)^2}}
\sin\left(\omega t-\theta\right) \equiv X\sin\left(\omega t-\theta\right)
\end{eqnarray*}
であり,この場合は
\begin{eqnarray*}
\frac{X}{a} = \tau
\end{eqnarray*}
この場合は,基礎を強制的に振動させた場合の基礎台の振幅$a$に対する物体の振動振幅$X$の比率であり,こちらは”変位に関する振動伝達率”と呼ばれる.力の伝達率とは意味合いが異なるが,その比率を表わす関係式は同一となる.
機械システムに生じる振動の低減
1自由度振動系で考察される
1) 強制振動応答の振幅特性
2) 力の振動伝達率
3) 変位の震度伝達率
を応用し,モデルパラメータである$m$,$c$,$k$を”うまく”設計する.こういった手法は,受動(振動)制御:Passive controlとも呼ばれる.これに対して,アクチュエーターを利用して振動制御が行われる場合もあり,それらは能動(振動)制御:Active controlと呼ばれる.
12.4 演習
(1) 変位振動計を用いて7Hzの正弦振動を10%以内の誤差で測定したい.振動計に減衰器がついていない場合,振動系の固有振動数はどのように選べばよいか.5%以内ではどうなるか?
(2) 5Hzの振動数をもつ調和振動を5%以内の誤差で測定できる変位計を作りたい.固有振動数をいくらにすればよいか.減衰のない系で考えよ.





