14.過渡応答
14.1 ステップ入力に対する1自由度系の応答
図14-1に示す質量$m$,ばね定数$k$の1自由度不減衰振動系に入力$f(t)$が作用した場合の過渡的な応答を考える.入力として,図14-2に示す大きさ$P$のステップ入力を加える.

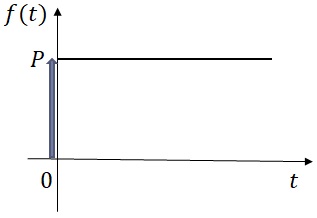
図14-1 1自由度不減衰振動系 図14-2 ステップ入力による励振
運動方程式は次式となる.
\begin{eqnarray*}
m\ddot{x} + kx = P \quad(t\geqq 0)
\end{eqnarray*}
\begin{eqnarray*}
\therefore \ddot{x} + p^2x = \frac{P}{m} \quad p=\sqrt{\frac{k}{m}}
\end{eqnarray*}
静止状態からの運動を考えると初期条件は,$t=0$で,$x=0$,$\dot{x}=0$とする.まず,右辺を零と置いた同次方程式の解$x_1$は,
\begin{eqnarray*}
x_1 = A\cos pt + B\sin pt
\end{eqnarray*}
となる.次に,右辺が一定値なので,特解$x_2$も定数となる必要があるので,
\begin{eqnarray*}
x_2 = C
\end{eqnarray*}
として,運動方程式に代入すると
\begin{eqnarray*}
p^2C = \frac{k}{m}C = \frac{P}{m}\quad \therefore C = \frac{P}{k}
\end{eqnarray*}
特解は次式となる.
\begin{eqnarray*}
x_2 = \frac{P}{k}
\end{eqnarray*}
よって,この系の一般解は次式となる.
\begin{eqnarray*}
x = x_1 + x_2 = A\cos pt + B\sin pt + \frac{P}{k}
\end{eqnarray*}
微分すると
\begin{eqnarray*}
\dot{x} = p\left(-A\sin pt + B\cos pt\right)
\end{eqnarray*}
となるので,初期条件を適用する.
\begin{eqnarray*}
\left.\begin{array}{l}
0 = A + \frac{P}{k} \\
0 = B
\end{array}\right\}
\end{eqnarray*}
即ち,$A = -\frac{P}{k}$,$B=0$より,系の応答は次式となる.
\begin{eqnarray*}
x = \frac{P}{k}\left(1 - \cos pt\right) = \delta_{st}\left(1-\cos pt\right)
\end{eqnarray*}
時間に対するこの系の応答を図示すると図14-3のようになる(グラフの記述に当たっては,グラフの形状だけでなく,最大,最大が生じる時刻とその値,あるいは,各軸と交わる点など特徴を表す点を具体的に描くようにする).
$P=P(t)=1$[N]のとき,単位ステップ応答と呼ばれ,入力の関数形を$u(t)$で表現し,$f(t) = Pu(t)$で任意の大きさのステップ入力を記述する.ここで,
\begin{eqnarray*}
u\left(t\right) =
\left\{\begin{array}{ll}
1 & (t\geqq 0) \\
0 & (t< 0)
\end{array}\right.
\end{eqnarray*}
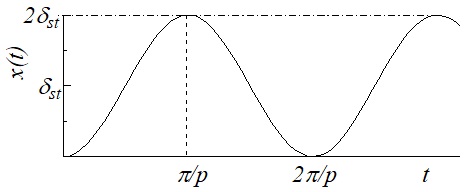
図14-3 ステップ入力に対する応答
14.2 インパルス入力と応答について
次に,図14-3に示すように$t=0$において,ステップ入力を加え,$t_1$秒後に零となる入力を考える.$t_1\rightarrow 0$とすると,瞬間的に入力が働いて無くなる”衝撃的な入力,いわゆるインパルス入力と考えることができる.
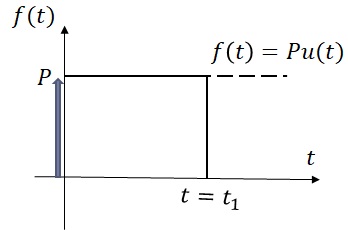
図14-4 一定時間のみのステップ入力
図14-4に示す入力は,2つのステップ入力の組合せで生成することができる.図14-5の左図の上側は$f(t) = Pu(t)$であり,下側は$f(t)=-P(t-t_1)$であり,両者を加えると右図のような入力となる.即ち,$t=0$でステップ入力$Pu(t)$を与え,$t=t_1$で大きさが同じで符号が逆のステップ入力$-Pu(t)$を加えれば,$t_1$秒以降の入力は零となる.即ち,この入力は次式となる.
\begin{eqnarray*}
f(t) = P\left\{u(t) - u(t-t_1)\right\}
\end{eqnarray*}
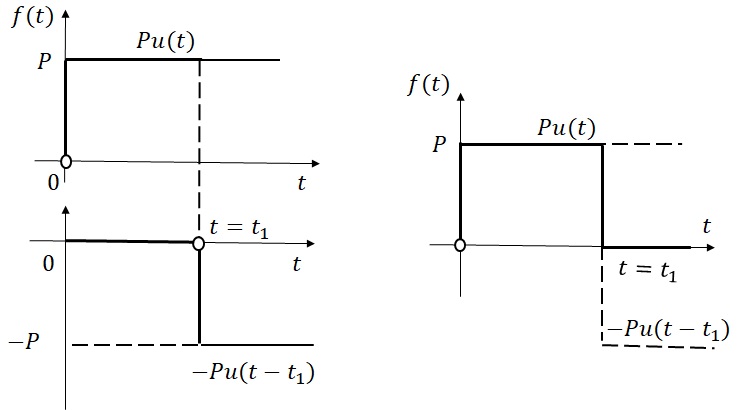
図14-5 インパルス入力の生成
この入力に対する応答は,各ステップ入力が各時間ごとに作用することになるので,各応答を重ね合わせればよいことになる.即ち前に示した図14-1の1自由度不減衰振動系に関しては次のような時刻歴応答を示すことになる.
\begin{eqnarray*}
x &=& \delta_{st}\left(1-\cos pt\right) + \delta_{st}\left\{1-\cos\left(t-t_1\right)\right\} \\
&=& \delta_{st}\left(-\cos pt + \cos pt\cos pt_1 + \sin pt\sin pt_1\right)
\end{eqnarray*}
ここで,$t_1=\Delta t$と置き直して整理する.
\begin{eqnarray*}
x = \delta_{st}\left\{\left(\cos p\Delta t -1 \right)\cos pt + \sin p\Delta t\sin pt\right\}
\end{eqnarray*}
$\Delta t\rightarrow0$とした時の応答を考えると,$\Delta t\ll 1$より
\begin{eqnarray*}
\cos p\Delta t \rightarrow 1\text{, } \sin p\Delta t\rightarrow p\Delta t
\end{eqnarray*}
となるので,
\begin{eqnarray*}
x = \delta_{st}p\Delta t\sin pt = \frac{P}{k}\sqrt{\frac{k}{m}}\sin pt = \frac{P\Delta t}{mp}\sin pt
\end{eqnarray*}
の形にまとめることができる.この形式の応答は初期速度のみが与えられた場合の応答と同じとなる.ここで,$P\Delta t$は力積であり,$\frac{P\Delta t}{m}$は,力積を加えた時の物体の速度と見なすことができる.よって,インパルス入力を受ける系は,$\frac{P\Delta t}{m}$の初速度を与えられた自由振動する系と見なすことができる.ここで,力の大きさを$P$としているが,$P=1$[N]とすると,$t=0$で,変位$x=0$,速度$\dot{x}=\frac{\Delta t}{m}$を与えたときの応答は,
\begin{eqnarray*}
x = \frac{\Delta t}{mp}\sin pt
\end{eqnarray*}
となり,この応答は大きさ$1$Nの力を瞬間的に加えた(単位衝撃入力が作用した)ときの応答,即ち,単位衝撃応答と見なすことができる.
14.3 任意入力に対する応答
単位衝撃入力が作用した時の応答を用いて,任意の大きさの入力に対する応答を表現することを考える.
図14-6上図に示す任意の時間的変化を有する入力波形を考える.この任意波形を例えば,下の図のようにある微小な時間間隔$d\tau$毎に分割し,時刻$t=\tau$において,$d\tau$の間,大きさ$f(\tau)=Pu(\tau)$の入力が加わった時の応答の変化$dx$は,14-3で得られた結果から,次式となると考えられる.
\begin{eqnarray*}
dx = \frac{f(\tau)d\tau}{mp}\sin p\left(t-\tau\right)
\end{eqnarray*}
ここで,$t=0$からの運動は,作用力に対する応答の重ね合わせであり,$f(\tau)$が連続で,$d\tau\rightarrow0$を考えると$t=0$から任意時刻$t$までの応答は次のような積分方程式で表せることになる.
\begin{eqnarray*}
x = x(t) = \int_0^t\frac{f(\tau)}{mp}\sin p\left(t-\tau\right)d\tau = \int_0^tf(\tau)\phi_n\left(t-\tau\right)d\tau
\end{eqnarray*}
ここで,
\begin{eqnarray*}
\phi_n\left(t\right)=\frac{1}{mp}\sin p\left(t\right)
\end{eqnarray*}
は,この系の単位衝撃応答関数と呼ばれ,系の伝達関数のラプラス逆変換したものとなる.また,この積分表現は,畳み込み積分(Convolution integral)と呼ばれ,任意の入力$f(t)$に対する系の応答を表現できる.

図14-6 任意入力の生成
単位衝撃応答関数(単位インパルス応答関数)
図14-1で示した1自由度不減衰振動系に対する運動方程式
\begin{eqnarray*}
m\ddot{x}(t) + kx(t) = f(t)
\end{eqnarray*}
を$t=0$で,$x(0)=0$,$\dot{x}(0)=0$(初期条件はすべて零)として,Laplace変換する.
\begin{eqnarray*}
L\left[m\ddot{x}(t) + kx(t)\right] = L\left[f(t)\right]
\end{eqnarray*}
ここで,
\begin{eqnarray*}
L\left[x(t)\right] = X(s)\text{, }L\left[f(t)\right]=F(s)
\end{eqnarray*}
とすると,
\begin{eqnarray*}
\left(x^2+k\right)X(s) = F(s)\quad\therefore X(s)=\frac{F(s)}{ms^2+k}
\end{eqnarray*}
単位衝撃入力(単位インパルス入力)のとき,$F(s)=1$より,$p^2=\frac{k}{m}$とおくと
\begin{eqnarray*}
X(s)=\frac{1}{ms^2+k}=\frac{1}{m}\frac{1}{2ip}\left(\frac{1}{s-ip} - \frac{1}{s+ip}\right)
\end{eqnarray*}
よって,ラプラス逆変換すると
\begin{eqnarray*}
x(t)=L^{-1}\left[X(s)\right] =\frac{1}{m}\frac{1}{2ip}\left(e^{ipt} - e^{-ipt}\right) = \frac{1}{mp}\sin pt
\end{eqnarray*}
ここで,
\begin{eqnarray*}
\frac{X(s)}{F(s)} = G(s)
\end{eqnarray*}
は,伝達関数と呼ばれるが,$F(s)=1$のときの応答は,$X(s)=G(s)$なので,出力が伝達関数そのものとなる.よって,系の伝達関数をLaplace逆変換したものが,単位衝撃(インパルス)応答関数となることがわかる.
1自由度粘性減衰系の応答
図14-7に示す1自由度粘性減衰系の運動方程式は次式となる.
\begin{eqnarray*}
m\ddot{x}(t) + +c\dot{x}(t) + kx(t) = f(t)
\end{eqnarray*}
$t=0$で,$x(0)=0$,$\dot{x}(0)=0$として,Laplace変換する.
\begin{eqnarray*}
&& \left(ms^2 +cs + k\right)X(s) = F(s) \\
&& \therefore G(s) = \frac{X(s)}{F(s)} = \frac{1}{ms^2 +cs + k} = \frac{1/m}{s^2 + 2\zeta p + p^2}
\end{eqnarray*}
ここで,$p=\sqrt{\frac{k}{m}}$,$\zeta=\frac{c}{2\sqrt{mk}}$である.$\zeta < 1$となる振動系を考えると
\begin{eqnarray*}
G(s) = \frac{1/m}{(s+\zeta p)^2 + (1-\zeta^2)p^2} = \frac{1}{m}\frac{1}{i2p\sqrt{1-\zeta^2}}\left(\frac{1}{s+\zeta p - ip\sqrt{1-\zeta^2}} - \frac{1}{s+\zeta p + ip\sqrt{1-\zeta^2}}\right)
\end{eqnarray*}
よって,逆変換することにより,この系の単位衝撃応答関数が次のように定まる.
\begin{eqnarray*}
\phi_n(t) &=& L^{-1}\left[G(s)\right] = \frac{1}{i2mp\sqrt{1-\zeta^2}}e^{-\zeta pt}\left(e^{ip\sqrt{1-\zeta^2}t} - e^{-ip\sqrt{1-\zeta^2}t}\right) \\
&=& \frac{1}{mp\sqrt{1-\zeta^2}}e^{-\zeta pt}\sin p\sqrt{1-\zeta^2}t
\end{eqnarray*}
従って,この系に任意入力$f(t)$が作用した時の応答は,次のように表現できる.
\begin{eqnarray*}
x &=& x(t) = \int_0^tf(\tau)\phi_n(t-\tau)d\tau = \int_0^tf(\tau)\frac{1}{mp\sqrt{1-\zeta^2}}e^{-\zeta p\left(t-\tau\right)}\sin\left\{p\sqrt{1-\zeta^2}(t-\tau)\right\}d\tau \\
&=& \frac{1}{mp\sqrt{1-\zeta^2}}\int_0^tf(\tau)e^{-\zeta p\left(t-\tau\right)}\sin\left\{p\sqrt{1-\zeta^2}(t-\tau)\right\} d\tau
\end{eqnarray*}
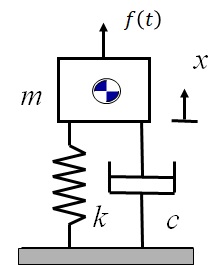
図14-7 1自由度粘性減衰系の応答
14.4 演習
(1) 図14-8に示すように,質量$m=30$kgの物体が,高さ$h=1$mのところから,ばね定数$k=30$N/cmのばねの上に落下する.落下後,物体のうける最大加速度をg単位で表せ.
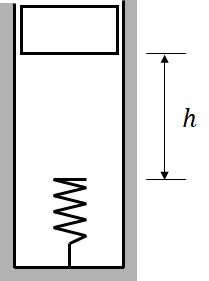
図14-8 ばね上に落下する物体に発生する加速度
(2) 不減衰1自由度ばね−質量系$(k,\ m)$に図13-6に示すように,$t_1$間に半周期正弦パルスが作用するとき,系の応答はいかになるか?ただし,$t_1=\pi/p = \pi/\sqrt{k/m}$とする.
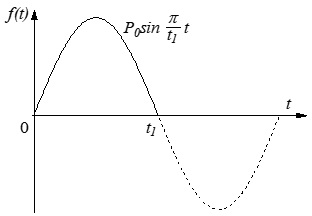
図14-9 半波正弦波入力に対する応答










