1.機械力学Ⅱについて
論理的に物事を決めていく際に必要な事柄とはどんなことであろうか?ここでは,物理現象を理解するために,数学的な手法を用いて考えるうえで必要となる事柄について考える.
根本原理や最初に全員が合意できる根源的な事柄,概念を決める必要がある.数学の世界では
公理:axiom その理論の出発点として,論証抜きで真だと仮定し,他の命題の前提とする根本命題
がそれにあたる.機械力学の講義では,以下の5つの項目を共通認識として定め,話を進める.
【機械力学における共通認識】
1.Newtonの第2法則(運動の法則)が成り立つ
2.作用・反作用の法則が成り立つ
3.一般に釣合位置(平衡状態)を中心として運動を仮定する
4.定めた座標方向に運動すると仮定する
5.一般に変形は微小であると仮定する
実際の現象において,これらが成立してるかどうかは別にして,基本的に上記の5項目を共通認識として今後は話を進める.但し,$3\sim5$に関しては,対象とする問題によっては該当しない場合についても今後考える場合もある.
ここで,Newtonの三法則は次の通りである.
Newtonの第1法則(慣性の法則)
物体に力が働いていないとき,物体は等速直線運動を続ける.
$\Rightarrow$ どんな種類の外力も働かない物体の運動を(静止している場合も含めて)等速直線運動として記述できる座標がつねに存在する.
$\cdots$ 慣性の法則が成り立つ座標系:慣性系
Newtonの第2法則(運動の法則)
力が働くと速度は変化し,このときの加速度は力の大きさに比例し,方向・向きは力の方向・向きと同一である.
$\Longrightarrow$ 力の定義:物体の運動状態を変化させる作用
Newtonの第3法則(作用・反作用の法則)
二つの物体が互いに力を及ぼしあうとき,作用と反作用は大きさが相等しく,同一直線状にあり,向きは互いに反対である.
1.1 モデル化
様々な”物理現象”を理解する,利用する,対策する,制御するなど多くの工学(あるいは科学)的捉え方が存在する.その特徴を抽出するためには,観察,測定,実験,…などなど,様々な定性的な評価,定量的な評価が必要となる.
$\Leftrightarrow$ 有力な手法として,その特性を表す数学モデルの利用というのがある!
動力学・振動現象:例として,自動車に対する数学モデル
質点系の力学では,質量 $m$ と力 $f$ を定義して,移動,走行などの運動を考えることができる.
.jpg) ⇒
⇒ 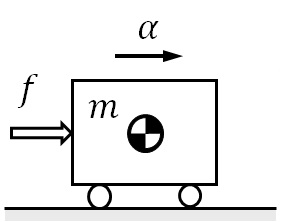
図1‐1 自動車走行運動のモデル化
すなわち,図1-1に示す路面を走行してる乗用車の走行運動について,加速度を$\alpha$として,
\begin{eqnarray*}
f=m\alpha
\end{eqnarray*}
なるNewtonの第2法則は,”乗用車の走行モデル”の運動方程式に対応することになる.
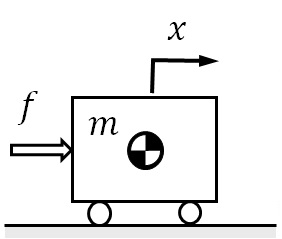
図1‐2 自動車の走行モデル(1自由度系)
ここで,水平面上を移動する自動車の運動を車体の重心位置を水平面と平行に取った絶対座標$x$を定義し,
$m$:車体質量(質点:重心に集中していると仮定)
$f$:駆動力 (重心位置に作用すると仮定)
を用いて,1自由度系でモデル化できることになり,モデル図を示すと図1-2のようになる.このとき,力を”駆動力”と称しているが,この意味について考えてみる.
ここでは,質点の運動を考えているので,この駆動力は,車両の重心に作用していると仮定している.しかしながら,車両は大きさを持っており,力の三要素の大きさ,方向,作用点(着力点)の作用点はどうなるかというと
駆動力 $\Rightarrow$ エンジントルクによるタイヤの回転に伴って発生する路面からの反力
が実際の現象に対応しているので,作用点を考えると図1-3のような描写が物理現象に対応しているように思われる.
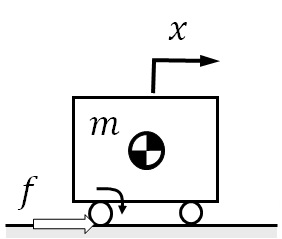
図1‐3 自動車の走行モデル(駆動力の表示)
作用点を気にしないで,運動方程式(基礎方程式)を示すと
\begin{eqnarray*}
m\ddot{x}=f
\end{eqnarray*}
逆に,駆動力の作用点をタイヤ接地点と考える場合は,前後輪のタイヤ接地点で作用・反作用の関係が考える必要が出てくる.
即ち,図1-4に示すように,前後輪の上下方向反力,重心位置などを考慮することにする場合は,座標系は水平方向$x$だけでなく,鉛直方向$y$,及び,面内回転$\theta$を考える必要がある.
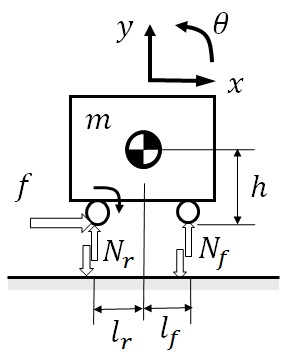
図1‐4 自動車の走行モデル(面内運動)
よって,この場合は,
$m$:車体質量(分布している)
$I_G$:車体慣性モーメント(紙面に垂直な軸の重心回り)
$f$:駆動力,駆動タイヤ(この場合は後輪)が路面から受ける力
$N_f$,$N_r$:路面反力,前後輪タイヤが路面から受ける垂直方向の力
$l_f$,$l_r$,$h$:重心から前後輪接地点距離,及び,重心高さ
を考え,座標系として
$x$:重心の水平方向絶対変位
$y$:重心の垂直方向絶対変位
$\theta$:重心回りの回転角変位(ここでは,反時計回りを正に取る)
を考えると運動方程式は次のようになる.
\begin{eqnarray*}
&& m\ddot{x}=f \\
&& m\ddot{y}=N_f+N_r-mg \\
&& I_G\ddot{\theta} = l_f\times N_f - l_r\times N_r+ h\times f
\end{eqnarray*}
従って,一般の面内(2次元の)運動は,座標位置2つと回転角度(姿勢と呼ばれる)の1つの計3つの自由度で表現されることになる.これが三次元空間に拡張される場合は,位置座標3つと座標系を表す3つの軸からの回転角で表した3つの姿勢角の計6個の自由度,即ち,6自由度系となる.
機械力学で対象とする系は更に次の2つの法則を持つ,力学要素を付加したモデルとなる.
Hookeの法則
粘性減衰の仮定
Newtonの第2法則を適用する際に必要となるモデルパラメータ(質量)とHookeの法則を適用するときに必要となるモデルパラメータ(ばね定数)を持つ系では,運動エネルギーとポテンシャルエネルギーのやり取りが可能となる系となるため,一般に振動現象が表現可能なモデルとなる.そのため,多くの機械システムで観察される(生じる)振動現象を調べる際のモデルとして広く使われることになる.
1.2 1自由度振動系
機械力学Ⅰで学んだように,自動車の上下(鉛直)方向の振動モデルは図1-5のようになる.
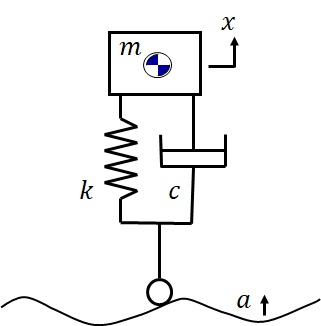
図1‐5 自動車上下振動1自由度モデル
ここで,各パラメータは次のように解釈される.
$m$:全車体質量(但し質点)
$x$:重心の上下方向変位
$k$:タイヤ,サスペンション等を考慮したばね定数(剛性)
$c$:タイヤ,サスペンション部ショックアブソーバーの減衰に対する粘性減衰係数
$a$:走行速度に依存して変化する路面からの上下(垂直)方向変位入力
各パラメータ値は,上記解釈に対応した形で数値化する必要がある.図1-5に対するFree-Body Diagramは図1-6のようになる.
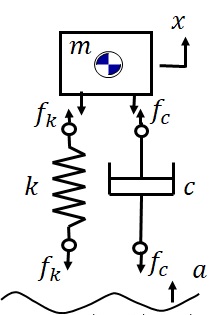
図1‐6 自動車1自由振動系に対するFBD
図1-6において,ばねの伸び(相対変位)は,$x-a$であり,ダッシュポットの伸び速度(相対速度)は,$\dot{x}-\dot{a}$となるので,ばね,ダッシュポットの発生力$f_k$,$f_c$は,Hookeの法則,及び,粘性減衰の関係から,それぞれ,次のようになる.
\begin{eqnarray*}
&& f_k=k\left(x-a\right) \\
&& f_c=c\left(\dot{x}-\dot{a}\right)
\end{eqnarray*}
よって,Newtonの第2法則より次式となる.
\begin{eqnarray*}
m\ddot{x} = -f_k-f_c =-k\left(x-a\right)-c\left(\dot{x}-\dot{a}\right)
\end{eqnarray*}
従って,この系の運動方程式は次のようになる.
\begin{eqnarray*}
m\ddot{x} + c\dot{x} + kx= kx+c\dot{a}
\end{eqnarray*}
この絶対座標系$x$に対して,$y=x-a$なる路面‐車体間の相対変位を考えると$x=y+a$より,次式となる.
\begin{eqnarray*}
&& m\left(\ddot{y}+\ddot{a}\right)=-ky-cy \\
&& \therefore m\ddot{y}+c\dot{y}+ky = -m\ddot{a}
\end{eqnarray*}
即ち,1自由度粘性減衰系の運動方程式となり,自由振動,強制振動,また,それらに伴う共振現象や固有振動数,減衰比と言った系の振動特性を調べることができるモデルとなる.
ここまでは,機械力学Ⅰで学んだモデル化である.機械を対象としているのであれば(多分)大きさは持つけれども,質量は重心に集中していると考え,局所的な変形も存在する(ことは明らかである)が,弾性的な変形をばね一個で,また,減衰特性を表現する(要素として)ダッシュポットを考えることにより,複雑な機械の振動の説明を試みてきた.それでは,運動が重心に集中していない,あるいは,変形を一個のばねやダッシュポットで表現できないとしたらどうなるか?あるいは,複雑な現象を十分に表現できないことが起こるとしたらどんな現象が現れる場合であろうか?
1.3 2自由度振動系
乗員乗車部と路面に接しているタイヤ部の上下方向の運動が必ずしも同じでない場合は,図1-7に示すように,車体をばね上とばね下に分け,相対的な運動を調べる場合がある.
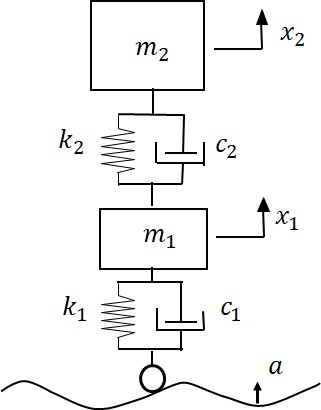
図1‐7 自動車上下振動2自由度系モデル
ばね上,ばね下の二か所のどこかに重心を定め,その上下方向の運動を考えるので自由度は2となるため,”2自由度系”と呼ばれる.また,図に示す座標変数,モデルパラメータ値の解釈は次のようになる.
$x_1$:ばね下重心位置変位
$m_1$:ばね下質量(主にタイヤでリム,軸径などが含まれる)
$k_1$:主にタイヤのばね剛性に対応するばね定数
$c_1$:主に,タイヤの減衰特性に対応する粘性減衰係数
$x_2$:ばね上重心位置変位
$m_2$:ばね上質量(タイヤ回りの質量を除く車体質量)
$k_1$:主にサスペンション部のばね剛性に対応するばね定数
$c_1$:主にサスペンション部ショックアブソーバーの減衰に対応する粘性減衰係数
$a$:走行速度に依存して変化する路面からの上下(垂直)方向変位入力
このモデルは,車体の左右方向と前後方向に配したタイヤ部とそれより上の車体部をまとめたものとなるので,”四分の一車体モデル”と呼ばれることもある.単純なモデルであるようにも見えるし,少し複雑になったようにも見えるが,本モデルで考えることにより,どんなこれまでには十分に表現できなかったことが分かるのであろうか?
前のモデルは,ばね上とばね下の部分の運動を2つの質点の上下方向運動として表現したものであるが,車体の大きさを考えると例えば,図1-8のようなモデルで表現される現象も乗用車の運動では散見される.
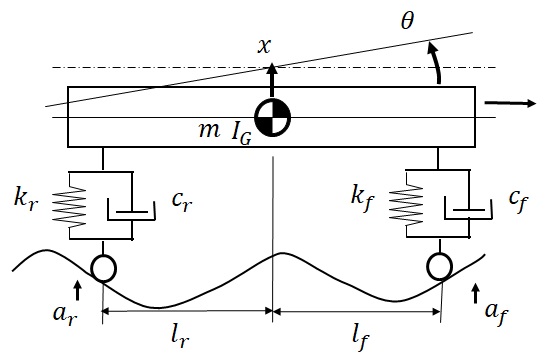
図1‐8 自動車上下-回転振動2自由度系モデル
このモデルでは,前後輪(あるいは左右輪)の路面との接地を考えるので,荷重のかかり方に応じて路面反力が変化するため,前後輪(あるいは左右輪)の接地位置と車体をつなぐサスペンション部の伸び(縮み)は,前後(左右)で必ずしも同じにならないため,車体の上下運動だけでなく,回転運動も生じることになる.この回転運動は,車体を横から見た場合には,”ピッチング運動”であり,前後方向から見た場合は,”ローリング運動”を上下振動と同時に調べていることになる.前と同様に,図に示す座標変数,モデルパラメータ値の解釈は次のようになる.
$x$:車体上下方向重心位置変位
$\theta$:重心回りの回転角変位
$m$:全車体質量
$I_G$:重心回りの全車体慣性モーメント(紙面に垂直な軸回り)
$k_f$,$k_r$:前後輪タイヤ,サスペンション部のばね剛性に対応したばね定数
$c_f$,$c_r$:前後輪タイヤ,サスペンションショックアブソーバー部に対応した粘性減衰係数
$l_f$,$l_r$:重心から前後輪タイヤ接地地点までの水平方向距離
$a_f$,$a_r$:走行速度に依存して変化する前後輪接地路面からの上下(垂直)方向変位入力
車体の特性を表すパラメータとして,質量と慣性モーメントを考えることから,車体を”剛体モデルでモデル化している”という表現もできる.
1.4 3自由度振動系
以上は2自由度系としてのモデルについて考えたが,前述の通り,面内運動では自由度は3つある.即ち,車両の上下方向だけでなく,前後あるいは左右方向の運動も考慮すると図1-9に示すようなモデルを考えることができる.
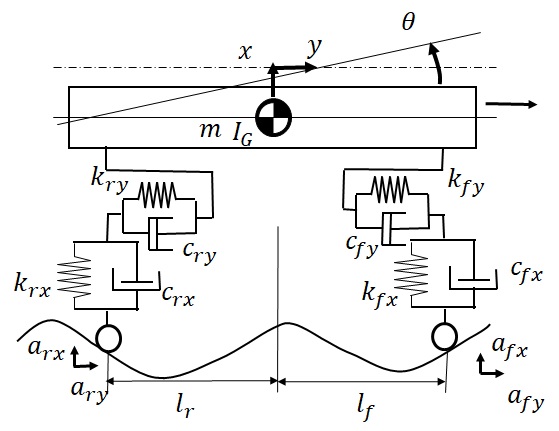
図1‐9 自動車面内振動3自由度系モデル
このモデルにおける座標変数,モデルパラメータ値の解釈は次のようになる.
$x$:車体上下方向重心位置変位
$y$:車体前後(左右)方向重心位置変位
$\theta$:重心回りの回転角変位
$m$:全車体質量
$I_G$:重心回りの全車体慣性モーメント(紙面に垂直な軸回り)
$k_{fx}$,$k_{rx}$:前後輪タイヤ,サスペンション部の上下方向ばね剛性に対応したばね定数
$c_{fx}$,$c_{rx}$:前後輪タイヤ,サスペンションショックアブソーバー部上下方向の減衰に対応した粘性減衰係数
$k_{fy}$,$k_{ry}$:前後輪タイヤ,サスペンション部の前後(左右))方向ばね剛性に対応したばね定数
$c_{fy}$,$c_{ry}$:前後輪タイヤ,サスペンションショックアブソーバー部前後(左右))方向の減衰に対応した粘性減衰係数
$l_f$,$l_r$:重心から前後輪タイヤ接地地点までの水平方向距離
$a_{fx}$,$a_{rx}$:走行速度に依存して変化する前後輪接地路面からの上下(垂直)方向変位入力
$a_{fy}$,$a_{ry}$:走行速度に依存して変化する前後輪接地路面からの前後(左右)方向変位入力
一般の乗用車では,前後や左右方向の振動は上下方向に比べて小さいが,ラグ付きタイヤで走行する農用トラクターや舗装されていない悪路では,上下,左右方向に起振力が加わることがあり,そういった現象を調べるためには面内振動を考慮したモデリングが必要になる.
1.5 4自由度振動系
これまで考えてきたモデルで表現されてきた現象を更に統合すると,車体のばね上の上下運動とばね下の上下運動を区別することと,車体の前輪部と後輪部に発生する反力を区別することのできるモデルが考えられる.図1-10は,タイヤ部を除くばね上の車体に関しては,重心の上下運動と重心回りの回転運動を考え,前後輪タイヤ部の各重心位置の上下運動を考慮したモデルで,自由度は4となる.
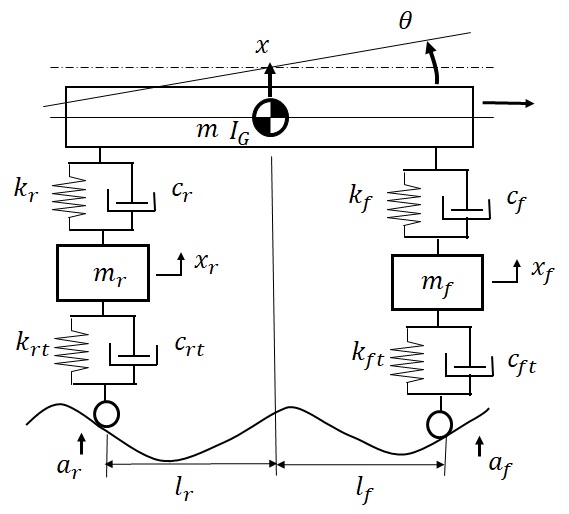
図1‐10 自動車面内振動4自由度系モデル
本モデルは,左右,あるいは,前後から見た車体の運動を表現していることから,二分の一車体モデルと呼ばれる.このモデルの座標変数,モデルパラメータ値は次のように解釈される.
$x$:ばね上(車体)重心位置の上下方向変位
$\theta$:ばね上(車体)の重心回りの回転角変位
$x_f$,$x_r$:前後輪に振り分けた各ばね下質量重心位置の上下方向変位
$m$:ばね上(車体)質量
$I_G$:ばね上(車体)重心回りの全車体慣性モーメント(紙面に垂直な軸回り)
$m_f$,$m_r$:前後輪に振り分けた各ばね下質量
$k_f$,$k_r$:サスペンション部のばね剛性に対応した各前後輪部側ばね定数
$c_f$,$c_r$:サスペンションショックアブソーバー部に対応した各前後輪部粘性減衰係数
$k_{ft}$,$k_{rt}$:前後輪タイヤ部のばね剛性に対応した各ばね定数
$c_{ft}$,$c_{rt}$:前後輪タイヤ部の減衰に対応した各粘性減衰係数
$l_f$,$l_r$:重心から前後輪タイヤ接地地点までの水平方向距離
$a_f$,$a_r$:走行速度に依存して変化する前後輪接地路面からの上下(垂直)方向変位入力
ばね上の上下と回転自由度と前後輪タイヤの上下方向を考えているので,4自由度となるが,前後輪の前後方向を加えると6自由度となり,前後輪の傾きを考えると更に,高次の自由度のモデルとなり得る.
このように,見たい現象に応じて様々なモデル化は可能であるが,現象の本質的な部分を具体的に表現できる簡易なモデリングを行うことができるかどうかが,エンジニアリングセンス,という事ができる.このセンスを磨くには,多くの現象に触れ,モデリング経験を積むことが重要である.
1.6 演習
(1) 図に示すように質量$m_1$,$m_2$ の物体が両端を各ばね定数$k_1$,$k_2$,$k_3$のばねを介して壁に繋がれている.この系に対するFree-body Diagramを示しなさい.また,2つの物体に対する運動方程式を求めなさい.
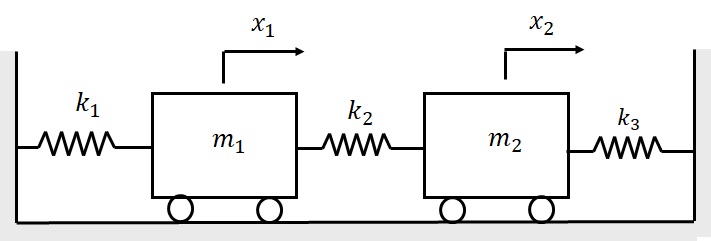
図1‐11 2自由度振動系
(2) 図1-12 は,質量$m_1$の台車がばね定数$k_1$のばねで壁に連結されており,台車上に設置された質量$m_2$の荷物がばね定数$k_2$のばねで台車と連結された系を表している.台車は地面に対して水平方向に滑らかに動くことができ,荷物もまた台車上を水平方向に滑らかに動くことができるとする.台車と荷物の水平方向変位をそれぞれ$x_1$,$x_2$として,この系に対するFree-body Diagramを示し,台車と荷物に対する運動方程式を求めなさい.
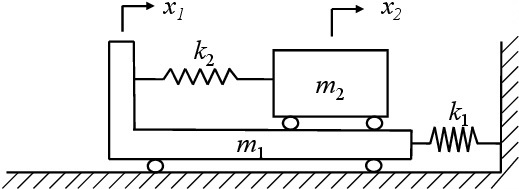
図1‐12 ばねで連結された2自由度振動系
.jpg) ⇒
⇒ 
.jpg) ⇒
⇒ 










