2.不減衰2自由度振動系の自由振動
2.1 2自由度振動系の運動方程式
図2-1に示すように,質量$m_1$,$m_2$の物体が3つのばねで連結されている不減衰2自由度振動系を取りあげる.まず,ばね定数を$k_1=k_2=k_3=k$,$m_1=m_2=m_3=m$の場合を考察する.まずは,初期条件を$x_1=5$m,$x_2=0$,$\dot{x}_1=\dot{x}_2=0$として,自由振動の式を導くことにする.

図2‐1 不減衰2自由度系
まず,運動方程式を求める.下向きの重力を考え,ばねに引張力が働くとして力の作用点と方向を考えてFree-body Diagramを書くと図2-2のようになる.
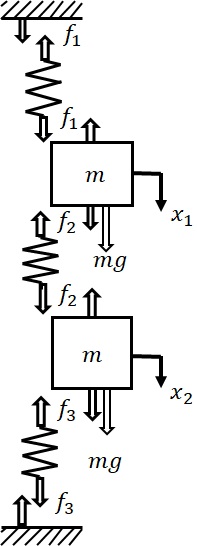
図2‐2 不減衰2自由度系に対するFree-body Diagram
ばねの伸びは,
\begin{eqnarray*}
\begin{array}{ll}
k_1\text{:} & x_1-0=x_1\\
k_2\text{:} & x_2-x_1 \\
k_3\text{:} & 0-x_2=-x_2
\end{array}
\end{eqnarray*}
となるので(マイナス符号は縮んだことを意味することになる),図に示すばね力(引張力)$f_1$,$f_2$,$f_3$は,Hookeの法則より
\begin{eqnarray*}
\left.\begin{array}{l}
f_1=k x_1\\
f_2=k\left(x_2-x_1\right)\\
f_3=-kx_2
\end{array}\right\}
\end{eqnarray*}
となる.
よって,2つの質量に対してNewtonの第2法則を適用すると次の運動方程式が定まる.
\begin{eqnarray*}
\left.\begin{array}{l}
m\ddot{x}_1=-f_1+f_2+mg=-k x_1+k\left(x_2-x_1\right)+mg\\
m\ddot{x}_2=-f_2+f_3+mg=-k\left(x_2-x_1\right)-kx_2+mg
\end{array}\right\}
\end{eqnarray*}
整理すると次式となる.
\begin{eqnarray*}
\left.\begin{array}{l}
m\ddot{x}_1+2k x_1-kx_2=mg\\
m\ddot{x}_2-kx_1+2kx_2=mg
\end{array}\right\}
\end{eqnarray*}
ここで,静的な釣り合い状態を考える.静的な状態は運動していないので,$\ddot{x}_1=\ddot{x}_2=0$であり,ばねが伸縮し重力と釣り合う状態ができる(はずである).この時,$x_1=x_{10}$,$x_2=x_{20}$とすると次式が成り立つ.
\begin{eqnarray*}
\left.\begin{array}{l}
2k x_{10}-kx_{20}= mg\\
-kx_{10}+2kx_{20} = mg
\end{array}\right\}
\end{eqnarray*}
よって,重力と釣り合ってばねが伸縮して静止している位置を原点とする座標系を考える.即ち,
\begin{eqnarray*}
&& x_1'=x_1-x_{10}\\
&& x_2'=x_2-x_{20}
\end{eqnarray*}
とすると,$\ddot{x}_{10}=\ddot{x}_{20}=0$より,運動方程式は次のようになる.
\begin{eqnarray*}
&& \left.\begin{array}{l}
m\ddot{x}_1'+2k \left(x_1'+x_{10}\right)-k\left(x_2'+x_{20}\right)=mg\\
m\ddot{x}_2'-k\left(x_1'+x_{10}\right)+2k\left(x_2'+x_{20}\right)=mg
\end{array}\right\}\\
&& \left.\begin{array}{l}
m\ddot{x}_1'+2k x_1'-kx_2' +2k x_{10}-kx_{20} =mg\\
m\ddot{x}_2'-kx_1'+2kx_2'-kx_{10}+2kx_{20}=mg
\end{array}\right\}
\end{eqnarray*}
よって,静的状態を原点とする座標$x_1'$,$x_2'$で表したこの系の運動方程式は次式となる.
\begin{eqnarray*}
\left.\begin{array}{l}
m\ddot{x}_1'+2k x_1'-kx_2' =0\\
m\ddot{x}_2'-kx_1'+2kx_2' = 0
\end{array}\right\}
\end{eqnarray*}
このように,運動方向に方向を変えず一定力(この場合は重力)が加わる系では,一定力との釣合位置を原点とする座標系で運動方程式を立てると一定力をキャンセルした方程式とすることができる.即ち,記号を置き直して,静的な釣り合い状態を原点とする座標系をそれぞれ$x_1$,$x_2$とすると,この系の運動方程式は次のようになる.
\begin{eqnarray*}
\left.\begin{array}{l}
m\ddot{x}_1+2k x_1-kx_2 = 0\\
m\ddot{x}_2-kx_1+2kx_2 = 0
\end{array}\right\}
\end{eqnarray*}
2.2 自由振動解
求められた運動方程式を共に$m$で除すと
\begin{eqnarray*}
\left.\begin{array}{l}
\ddot{x}_1+\frac{2k}{m}x_1-\frac{k}{m}x_2=0\\
\ddot{x}_2-\frac{k}{m}x_1+\frac{2k}{m}x_2=0
\end{array}\right\}
\end{eqnarray*}
この2式は,定数係数の線形連立常微分方程式なので,特性根を$\lambda$,未定係数を$X_1$,$X_2$として,次の解を仮定することができる.
\begin{eqnarray*}
x_j=X_je^{\lambda t} \quad (j=1\text{, }2)
\end{eqnarray*}
ここで,$\dot{x}_j=\lambda X_je^{\lambda t}$,$\ddot{x}_j=\lambda^2X_je^{\lambda t}$より,次式を得る.
\begin{eqnarray*}
\left.\begin{array}{l}
\left\{\left(\lambda^2+\frac{2k}{m}\right)X_1-\frac{k}{m}X_2\right\}e^{\lambda t}=0\\
\left\{-\frac{k}{m}X_1+\left(\lambda^2+\frac{2k}{m}\right)X_2\right\}e^{\lambda t}=0
\end{array}\right\}
\end{eqnarray*}
$e^{\lambda t}\neq 0$より,$X_1$,$X_2$を未知数とする次の連立一次方程式を得る.
\begin{eqnarray*}
\left.\begin{array}{l}
\left(\lambda^2+\frac{2k}{m}\right)X_1-\frac{k}{m}X_2=0\\
-\frac{k}{m}X_1+\left(\lambda^2+\frac{2k}{m}\right)X_2=0
\end{array}\right\}
\end{eqnarray*}
この方程式の解は,明らかであるが,行列形式で表示して,解$X_1$,$X_2$を求めることにする.
\begin{eqnarray*}
\left[\begin{array}{cc}
\lambda^2+\frac{2k}{m} & -\frac{k}{m}\\
-\frac{k}{m} & \lambda^2+\frac{2k}{m}
\end{array}\right]\left[\begin{array}{c}
X_1 \\ X_2 \end{array}\right]=\left[\begin{array}{c}
0 \\ 0 \end{array}\right]
\end{eqnarray*}
係数行列の行列式を$\Delta$として,左から逆行列をかけることにより次式を得る.
\begin{eqnarray*}
\left[\begin{array}{c}
X_1 \\ X_2 \end{array}\right]=
\frac{1}{\Delta}\left[\begin{array}{cc}
\lambda^2+\frac{2k}{m} & \frac{k}{m}\\
\frac{k}{m} & \lambda^2+\frac{2k}{m}
\end{array}\right]\left[\begin{array}{c}
0 \\ 0 \end{array}\right]=
\left[\begin{array}{c}
0 \\ 0 \end{array}\right]
\end{eqnarray*}
即ち,自明な解(と言われる)$X_1=X_2=0$となる.この場合は,仮定した変位そのものが零となるので振動しないことを意味し,運動が起こらない,つまり(自由)振動を生じない場合の解,つまり,無意味な解となる.与えられた運動方程式において,無意味でない解を得るには,この解が得られない条件を考えればよい.それは,前に示したような変形ができない条件,逆行列をかけて,$X_1$と$X_2$を求めることができない条件,即ち,$\Delta =0$(逆行列が存在しない条件)である.ここで,
\begin{eqnarray*}
&& \quad \left|\begin{array}{cc}
\lambda^2+\frac{2k}{m} & -\frac{k}{m}\\
-\frac{k}{m} & \lambda^2+\frac{2k}{m}
\end{array}\right|=0 \\
&& \quad \left(\lambda^2+\frac{2k}{m}\right)^2-\left(\frac{k}{m}\right)^2=0 \\
&& \therefore \left(\lambda^2+\frac{k}{m}\right)\left(\lambda^2+\frac{3k}{m}\right)=0
\end{eqnarray*}
となり,$\lambda$に関する4次方程式,あるいは,$\lambda^2$に関する2次方程式が定まる.この方程式は,特性方程式と呼ばれ,この場合は次の4つ(あるいは2組)の特性根を持つことになる.
\begin{eqnarray*}
\lambda=\pm i\sqrt{\frac{k}{m}}\text{, }\pm i\sqrt{\frac{3k}{m}}
\end{eqnarray*}
ここで,$i$は虚数単位である.不減衰振動系では,このように特性根は純虚数となるので,振動問題では,$x_j=X_je^{\lambda t}$を$x_j=X_je^{i\omega t}$とき,角振動数$\omega$に関する方程式を考える場合がある.この場合の方程式は,振動数方程式と呼ばれ,今回の場合は,
\begin{eqnarray*}
\Delta=\Delta(\omega)=\left(\omega^2-\frac{k}{m}\right)\left(\omega^2-\frac{3k}{m}\right)=0
\end{eqnarray*}
となる.そこで,
\begin{eqnarray*}
\lambda_1=i\omega_1=i\sqrt{\frac{k}{m}}\text{, }\lambda_2=i\omega_2=i\sqrt{\frac{3k}{m}}
\end{eqnarray*}
と置く.$X_1$,$X_2$が共に零とならない場合として,特性根を定めたが,$X_1$と$X_2$について何か考えるべき特性があるのであろうか?
元々の方程式中に$\lambda^2$があるので,実際にその関係式を代入して,どんな関係があるか調べてみる.即ち,$\lambda_1^2=-\frac{k}{m}$を元の式に代入すると,
\begin{eqnarray*}
&& \quad \left.\begin{array}{l}
\left\{\left(-\frac{k}{m}\right)+\frac{2k}{m}\right\}X_1 - \frac{k}{m}X_2=0 \\
-\frac{k}{m}X_1 + \left\{\left(-\frac{k}{m}\right) + \frac{2k}{m}\right\}X_2=0
\end{array}\right\}\\
&& \quad \left.\begin{array}{l}
\frac{k}{m}X_1 - \frac{k}{m}X_2=0 \\
-\frac{k}{m}X_1 + \frac{k}{m}X_2=0
\end{array}\right\}\\
&& \therefore X_1=X_2
\end{eqnarray*}
となる.一方,$\lambda_2^2=-\frac{3k}{m}$のとき,
\begin{eqnarray*}
&& \quad \left.\begin{array}{l}
\left\{\left(-3\frac{k}{m}\right)+\frac{2k}{m}\right\}X_1 - \frac{k}{m}X_2=0 \\
-\frac{k}{m}X_1 + \left\{\left(-3\frac{k}{m}\right) + \frac{2k}{m}\right\}X_2=0
\end{array}\right\}\\
&& \therefore X_1=-X_2
\end{eqnarray*}
となる.即ち,
\begin{eqnarray*}
\left.\begin{array}{ll}
\lambda_1=\pm i\omega_1=\pm i\sqrt{\frac{k}{m}}\text{のとき} & X_2=X_1\\
\lambda_2=\pm i\omega_2=\pm i\sqrt{\frac{3k}{m}}\text{のとき} & X_2=-X_1
\end{array}\right\}
\end{eqnarray*}
の関係が成立していることが分かる.従って,$x_1$,$x_2$に対する一般解は4個の未定係数を用いて次のように表わすことができる.
\begin{eqnarray*}
\left.\begin{array}{l}
x_1 = X_{11}e^{i\sqrt{\frac{k}{m}}t}+X_{12}e^{-i\sqrt{\frac{k}{m}}t}+X_{13}e^{i\sqrt{\frac{3k}{m}}t}+X_{14}e^{-i\sqrt{\frac{3k}{m}}t} \\
x_2 = 1\times\left(X_{11}e^{i\sqrt{\frac{k}{m}}t}+X_{12}e^{-i\sqrt{\frac{k}{m}}t}\right)+\left(-1\right)\times\left(X_{13}e^{i\sqrt{\frac{3k}{m}}t}+X_{14}e^{-i\sqrt{\frac{3k}{m}}t}\right)
\end{array}\right\}
\end{eqnarray*}
変形すると
\begin{eqnarray*}
\left.\begin{array}{l}
x_1 = \left(X_{11}+X_{12}\right)\cos\sqrt{\frac{k}{m}}t+i\left(X_{11}-X_{12}\right)\sin\sqrt{\frac{k}{m}}t+\left(X_{13}+X_{14}\right)\cos\sqrt{\frac{3k}{m}}t+i\left(X_{13}-X_{14}\right)\sin\sqrt{\frac{3k}{m}}t\\
x_2 = \left(X_{11}+X_{12}\right)\cos\sqrt{\frac{k}{m}}t+i\left(X_{11}-X_{12}\right)\sin\sqrt{\frac{k}{m}}t-\left\{\left(X_{13}+X_{14}\right)\cos\sqrt{\frac{3k}{m}}t+i\left(X_{13}-X_{14}\right)\sin\sqrt{\frac{3k}{m}}t\right\}
\end{array}\right\}
\end{eqnarray*}
よって,未定係数を置き直すことにより,次の一般解を得る.
\begin{eqnarray*}
\left.\begin{array}{l}
x_1 = a_1\cos\sqrt{\frac{k}{m}}t+b_1\sin\sqrt{\frac{k}{m}}t+a_2\cos\sqrt{\frac{3k}{m}}t+b_2\sin\sqrt{\frac{3k}{m}}t\\
x_2 = a_1\cos\sqrt{\frac{k}{m}}t+b_1\sin\sqrt{\frac{k}{m}}t-\left(a_2\cos\sqrt{\frac{3k}{m}}t+b_2\sin\sqrt{\frac{3k}{m}}t\right)
\end{array}\right\}
\end{eqnarray*}
時間で微分して,各速度を求めると次のようになる.
\begin{eqnarray*}
\left.\begin{array}{l}
\dot{x}_1 = \sqrt{\frac{k}{m}}\left(-a_1\sin\sqrt{\frac{k}{m}}t+b_1\cos\sqrt{\frac{k}{m}}t\right)+\sqrt{\frac{3k}{m}}\left(-a_2\sin\sqrt{\frac{3k}{m}}t+b_2\cos\sqrt{\frac{3k}{m}}t\right)\\
\dot{x}_2 = \sqrt{\frac{k}{m}}\left(-a_1\sin\sqrt{\frac{k}{m}}t+b_1\cos\sqrt{\frac{k}{m}}t\right)-\sqrt{\frac{3k}{m}}\left(-a_2\sin\sqrt{\frac{3k}{m}}t+b_2\cos\sqrt{\frac{3k}{m}}t\right)
\end{array}\right\}
\end{eqnarray*}
よって,初期条件$t=0$で,$x_1=5$m,$x_2=0$,$\dot{x}_1=\dot{x}_2=0$より次式を得る.
\begin{eqnarray*}
&& \left.\begin{array}{l}
a_1+a_2=5 \\
a_1-a_2=0 \\
\sqrt{\frac{k}{m}}b_1+\sqrt{\frac{3k}{m}}b_2=0 \\
\sqrt{\frac{k}{m}}b_1-\sqrt{\frac{3k}{m}}b_2=0
\end{array}\right\}\\
&& \therefore a_1=a_2=2.5\text{, }b_1=b_2=0
\end{eqnarray*}
を得る.よって,この系は次の式で示すような時間的な変動を起こす,
\begin{eqnarray*}
\left.\begin{array}{l}
x_1=2.5\left(\cos\sqrt{\frac{k}{m}}t + \cos\sqrt{\frac{3k}{m}}t\right) \\
x_2=2.5\left(\cos\sqrt{\frac{k}{m}}t - \cos\sqrt{\frac{3k}{m}}t\right)
\end{array}\right\}
\end{eqnarray*}
即ち,$\sqrt{\frac{k}{m}}$と$\sqrt{\frac{3k}{m}}$という2つの角振動数で振動するような自由振動応答をすることになる.即ち,上式がこの系の自由振動応答解である.
2.3 固有角振動数と固有モード
自由振動応答解から分かるように,特性根に$\lambda_i(i=1\text{, }2)$対し,角振動数に対応する$\omega_i(i=1\text{, }2)$は,自由振動の特性を表わすことから,固有角振動数と呼ばれ,一般に,値の小さい順から,第1次,第2次固有角振動数とされる.特性根,固有角振動数は,線形代数で学ぶ固有値に対応しており,この値を元の式に代入して定まる関係は,固有ベクトルに対応し,ここでは次のような振幅比として定まった.つまり,
\begin{eqnarray*}
\left.\begin{array}{ll}
\omega_1=\sqrt{\frac{k}{m}}\text{に対して}&\frac{X_2}{X_1}=1 \\
\omega_2=\sqrt{\frac{3k}{m}}\text{に対して}&\frac{X_2}{X_1}=-1
\end{array}\right\}
\end{eqnarray*}
なる固有角振動数に対応した固有の振幅比が定まる.これは,”振動する様子を表している”と考えることもできるので,固有モード,あるいは,振動モード,と呼ばれる.
第1次と第2次の固有モードに対応する振幅比の分布のイメージ図を図2-3に示す.
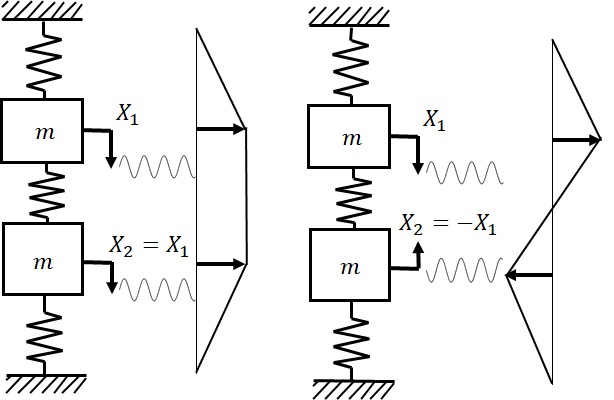
図2‐3 固有モードに対応する振幅比の分布イメージ
振幅比が$1$である一次モードは,2つの地点は,同じ振幅で角振動数$\omega_1=\sqrt{\frac{k}{m}}$で振動することを意味している.一方,振幅比が$-1$である二次モードは,振幅の大きさは同じであるが,符号が逆で,角振動数$\omega_2=\sqrt{\frac{3k}{m}}$で振動することを意味することになるので,こちらは2つの地点は逆位相,あるいは,位相が$\pi$,180度ずれた振動をすることを意味することになる.
更にこの2つの固有モードについて考えてみる.図2-4(a)に示すように,$\frac{X_2}{X_1}=1$,即ち,1次モードの時には,2点の位置における振幅が同じであり,かつ,同じ振動数で振動することから,中央部のばねの伸びはゼロになる.ばねの伸びが零となる場合のばね定数を逆に考えると,値が$\infty$となるときであるので,1次モードは,中央部のばね定数が無限大となった,とも考えられる.これらに対応して2点に分布している質量は,剛体のように一体となって振動していると見なせるので,質量が$2m$となったとも考えられる.よって,1次モードの振動系は,質量$2m$の物体がばね定数$k$のばねで両側から連結されたいる1自由度振動系と見なすこともできる.したがって,質量中心からの変位を$y_1$とおくと,この場合の運動方程式は次のようになる.
\begin{eqnarray*}
&& \quad 2m\ddot{y}_1+2ky_1=0 \\
&& \therefore \ddot{y}_1+\frac{k}{m}y_1=0
\end{eqnarray*}
この場合の固有角振動数は当然の如く,$\omega_1=\sqrt{\frac{k}{m}}$である.
一方,振幅比が$\frac{X_2}{X_1}=-1$のとき,即ち,2次モードの時には,2つの質量が近づいたり,離れたりといった中央部ばねの中心があたかも固定されているかのような振動であるので,ばね中央部から上側と下側に同じばね定数$k'$のばねが直列につながっていると考え,それが合成されたばね定数がもともとのばね定数$k$とすると
\begin{eqnarray*}
&& \quad \frac{1}{k}=\frac{1}{k'}+\frac{1}{k'} \\
&& \therefore k'=2k
\end{eqnarray*}
となり,中央部から上下両側にばね定数$2k$のばねがあり,中央が固定された状態で運動しているように見なすことができる.即ち,上下両方の質量の変位を$y_2$として,両者とも次の同じ運動方程式となる.
\begin{eqnarray*}
&& \quad m\ddot{y}_2+3ky_2=0 \\
&& \therefore \ddot{y}_2+\frac{3k}{m}y_2=0
\end{eqnarray*}
即ち,固有角振動数$\omega_2=\sqrt{\frac{3k}{m}}$の1自由度系が上下対称に並んでいる系と見なすことができる.但し,2つは互いに方向が逆(逆位相)の運動をする.

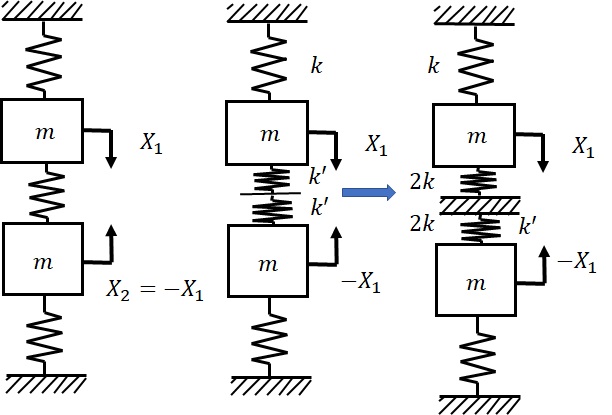
(a)1次モード (b)2次モード
図2‐4 2つの固有モードにおける質量,ばねの寄与
2.4 運動方程式からの考察
元々の運動方程式に立ち返って考えてみる.
\begin{eqnarray*}
\left.\begin{array}{l}
m\ddot{x}_1+2k x_1-kx_2=0\\
m\ddot{x}_2-kx_1+2kx_2=0
\end{array}\right\}
\end{eqnarray*}
2式を足すと
\begin{eqnarray*}
m\left(\ddot{x}_1+\ddot{x}_2\right)+k\left(x_1+x_2\right)=0
\end{eqnarray*}
ここで,元々もの系の重心位置は,
\begin{eqnarray*}
x_G=\frac{x_1+x_2}{2}
\end{eqnarray*}
となるので,出てきた方程式は
\begin{eqnarray*}
&& m\left(2\ddot{x}_G\right)+k\left(2x_G\right)=0 \\
&& \therefore m\ddot{x}_G + kx_G=0
\end{eqnarray*}
となり,この系の重心の運動を表す運動方程式となる.一方,第2式から第1式を引くと
\begin{eqnarray*}
m\left(\ddot{x}_2-\ddot{x}_1\right)+3k\left(x_2-x_1\right)=0
\end{eqnarray*}
となる.よって,$x_1$に対する$x_2$の相対変位$x_R=x_2-x_1$を考えると,
\begin{eqnarray*}
m\ddot{x}_R+3kx_R=0
\end{eqnarray*}
は,この相対変位に関する運動を表す運動方程式となることがわかる.
2.5 演習
(1) 図2-5に示す2自由度振動系において,$m_1=m_2=1$ [kg],$k_1=k_2=1$ [N/m]とする.$t=0$ [s]において,$x_1=x_2=0$ [m],$x_1=1$[m/s],$x_2=0$[m/s]を与えた場合の自由振動応答を時間の関数として示せ.

図2‐5 一方のみが壁でばね支持された不減衰2自由度振動系の振動
(2) 図2-6は,質量$m_1$の台車がばね定数$k_1$のばねで壁に連結されており,台車上に設置された質量$m_2$の荷物がばね定数$k_2$のばねで台車と連結された系を表している.台車は地面に対して水平方向に滑らかに動くことができ,荷物もまた台車上を水平方向に滑らかに動くことができるとする.$m_1=10$[kg],$m_2=1$[kg],$k_1=1.75$[kN/m],$k_2=1.5$[kN/m]の系に対して,荷物$m_2$に初期変位$0.1$[m]を与え,静かに放したときの自由振動応答を求めよ.
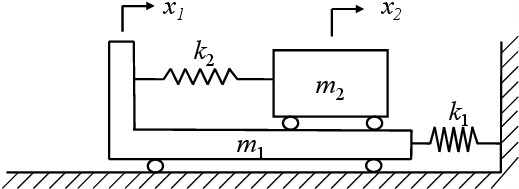
図2‐6 ばねで連結された2自由度振動系







