3.不減衰2自由度振動系の自由振動(回転運動)
図3-1は,長さ$l$の糸で繋がれた同じ質量$m$の2つの物体(質点)が長さ$l$の糸で吊り下げられたモデルを表しており,微小振動を仮定すると,系の2つの固有角振動数は,
\begin{eqnarray*}
p=\sqrt{\frac{g}{l}\left(2\mp \sqrt{2}\right)}
\end{eqnarray*}
で与えられる.実際に運動方程式を求め,固有角振動数と固有モードを求めてみる.
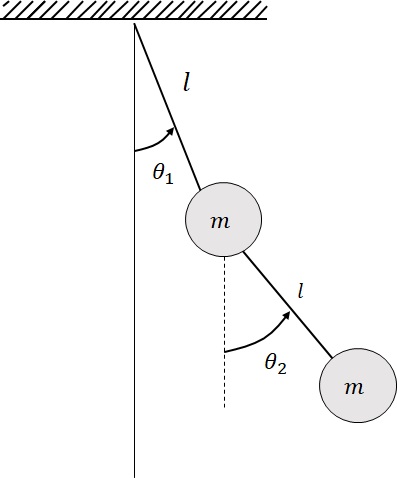
図3-1 2重振り子の自由振動
3.1 2重振り子の運動方程式
鉛直下向きを正に$x$軸,水平方向右向きを正に$y$軸とする$xy$座標系を考え,$x$軸を基準とする回転角変位を反時計回りを正として$\theta_1$,$\theta_2$とする.また,2つの質点の座標位置をそれぞれ$(x_1,\ y_1)$,$(x_2,\ y_2)$として,Free-body Diagramを考えると図3-2のようになる.ここで,図中に示すように,各糸には$T_1$,$T_2$の張力が発生する.
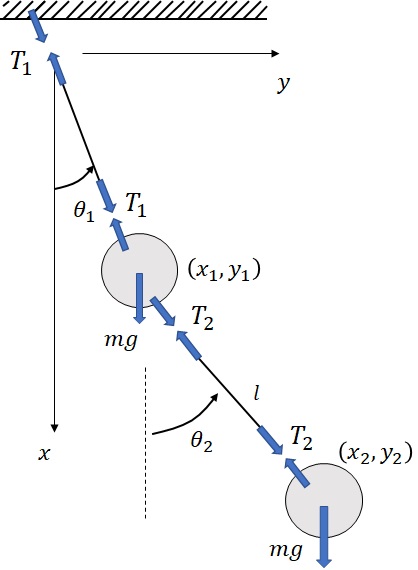
図3-2 不減衰2自由度系に対するFree-body Diagram
よって,$xy$方向の分力と各質点に作用する重力から2つの質点に対する$xy$方向の運動方程式を次のように考えることができる.
\begin{eqnarray*}
\left.\begin{array}{l}
m\ddot{x}_1 = mg + T_2\cos\theta_2 - T_1\cos\theta_1 \\
m\ddot{y}_1 = T_2\sin\theta_2 - T_1\sin\theta_1
\end{array}\right\}
\end{eqnarray*}
\begin{eqnarray*}
\left.\begin{array}{l}
m\ddot{x}_2 = mg - T_2\cos\theta_2\\
m\ddot{y}_2 = -T_2\sin\theta_2
\end{array}\right\}
\end{eqnarray*}
一方,各質点の座標は,角度$\theta_1$,$\theta_2$を用いて次のように表すことができる.
\begin{eqnarray*}
&& \left.\begin{array}{l}
x_1 = l\cos\theta_1\\
y_1=l\sin\theta_1
\end{array}\right\} \\
&& \left.\begin{array}{l}
x_2 = l\left(\cos\theta_1+\cos\theta_2 \right)\\
y_2=l\left(\sin\theta_1+\sin\theta_2 \right)
\end{array}\right\}
\end{eqnarray*}
$\theta_j=\theta_j(t)(j=1,2)$であることを考慮して時間微分して,速度成分を求める.
\begin{eqnarray*}
&& \left.\begin{array}{l}
\dot{x}_1 = -l\dot{\theta}_1\sin\theta_1\\
\dot{y}_1=l\dot{\theta}_1\cos\theta_1
\end{array}\right\}\\
&&\left.\begin{array}{l}
\dot{x}_2 = -l\left(\dot{\theta}_1\sin\theta_1+\dot{\theta}_2\sin\theta_2 \right)\\
\dot{y}_2=l\left(\dot{\theta}_1\cos\theta_1+\dot{\theta}_2\cos\theta_2 \right)
\end{array}\right\}
\end{eqnarray*}
さらに,微分して加速度成分を求める.
\begin{eqnarray*}
\left.\begin{array}{l}
\ddot{x}_1 = -l\ddot{\theta}_1\sin\theta_1-l\dot{\theta}_1^2\cos\theta_1\\
\dot{y}_1 = l\ddot{\theta}_1\cos\theta_1 - l\dot{\theta}_1^2\sin\theta_1
\end{array}\right\}
\end{eqnarray*}
\begin{eqnarray*}
\left.\begin{array}{l}
\ddot{x}_2 = -l\left(\ddot{\theta}_1\sin\theta_1 + \dot{\theta}_1^2\cos\theta_1 + \ddot{\theta}_2\sin\theta_2+\dot{\theta}_2^2\cos\theta_2 \right)\\
\ddot{y}_2 = l\left(\ddot{\theta}_1\cos\theta_1-\dot{\theta}_1^2\sin\theta_1 + \ddot{\theta}_2\cos\theta_2 -\dot{\theta}_2^2\sin\theta_2\right)
\end{array}\right\}
\end{eqnarray*}
よって,これらを運動方程式に代入すると次式となる.
\begin{eqnarray*}
\left.\begin{array}{l}
-ml\left(\ddot{\theta}_1\sin\theta_1+\dot{\theta}_1^2\cos\theta_1\right)=mg+T_2\cos\theta_2-T_1\cos\theta_1 \\
ml\left(\ddot{\theta}_1\cos\theta_1 - \dot{\theta}_1^2\sin\theta\right)=T_2\sin\theta_2-T_1\sin\theta_1
\end{array}\right\}
\end{eqnarray*}
\begin{eqnarray*}
\left.\begin{array}{l}
-ml\left(\ddot{\theta}_1\sin\theta_1 + \dot{\theta}_1^2\cos\theta_1 + \ddot{\theta}_2\sin\theta_2+\dot{\theta}_2^2\cos\theta_2 \right)=mg - T_2\cos\theta_2 \\
ml\left(\ddot{\theta}_1\cos\theta_1-\dot{\theta}_1^2\sin\theta_1 + \ddot{\theta}_2\cos\theta_2 -\dot{\theta}_2^2\sin\theta_2\right) = -T_2\sin\theta_2
\end{array}\right\}
\end{eqnarray*}
第3,4式より
\begin{eqnarray*}
-ml\left(\ddot{\theta}_1\sin\theta_1 + \dot{\theta}_1^2\cos\theta_1 + \ddot{\theta}_2\sin\theta_2+\dot{\theta}_2^2\cos\theta_2 \right)\sin\theta_2 - ml\left(\ddot{\theta}_1\cos\theta_1-\dot{\theta}_1^2\sin\theta_1 + \ddot{\theta}_2\cos\theta_2 -\dot{\theta}_2^2\sin\theta_2\right)\cos\theta_2 = =mg\sin\theta_2 - T_2\cos\theta_2\sin\theta_2+T_2\sin\theta_2\cos\theta_2
\end{eqnarray*}
\begin{eqnarray*}
\therefore -ml\left(\ddot{\theta}_1\sin\theta_1\sin\theta_2 + \dot{\theta}_1^2\cos\theta_1\sin\theta_2 + \ddot{\theta}_2\sin^2\theta_2+\dot{\theta}_2^2\sin\theta_2\cos\theta_2 + \ddot{\theta}_1\cos\theta_1\cos\theta_2-\dot{\theta}_1^2\sin\theta_1\cos\theta_2 + \ddot{\theta}_2\cos^2\theta_2 -\dot{\theta}_2^2\sin\theta_2\cos\theta_2\right) = mg\sin\theta_2
\end{eqnarray*}
故に,次のような一つ目の運動方程式が得られる.
\begin{eqnarray*}
ml\left\{\ddot{\theta}_1\cos\left(\theta_2-\theta_1\right)+ \dot{\theta}_1^2\sin\left(\theta_2-\theta_1\right) + \ddot{\theta}_2\ \right\} + mg\sin\theta_2 = 0
\end{eqnarray*}
また,第3,4式から張力$T_2$を次のように表すことができる.
\begin{eqnarray*}
-ml\left(\ddot{\theta}_1\sin\theta_1 + \dot{\theta}_1^2\cos\theta_1 + \ddot{\theta}_2\sin\theta_2+\dot{\theta}_2^2\cos\theta_2 \right)\cos\theta_2 + ml\left(\ddot{\theta}_1\cos\theta_1-\dot{\theta}_1^2\sin\theta_1 + \ddot{\theta}_2\cos\theta_2 -\dot{\theta}_2^2\sin\theta_2\right)\sin\theta_2 = mg\cos\theta_2 - T_2\cos^2\theta_2 -T_2\sin^2\theta_2
\end{eqnarray*}
\begin{eqnarray*}
\therefore T_2 = mg\cos\theta_2 + ml\left\{-\ddot{\theta}_1\sin\left(\theta_2-\theta_1\right)+\dot{\theta}_1^2\cos\left(\theta_2-\theta_1\right)+\dot{\theta}_2^2\right\}
\end{eqnarray*}
同様に,第1,2式より,張力$T_1$を消去すると次式となる.
\begin{eqnarray*}
-ml\left(\ddot{\theta}_1\sin\theta_1+\dot{\theta}_1^2\cos\theta_1\right)\sin\theta_1- ml\left(\ddot{\theta}_1\cos\theta_1 - \dot{\theta}_1^2\sin\theta\right)\cos\theta_1 = mg\sin\theta_1+T_2\cos\theta_2\sin\theta_1-T_1\cos\theta_1\sin\theta_1 -T_2\sin\theta_2\cos\theta_1+T_1\sin\theta_1\cos\theta_1
\end{eqnarray*}
\begin{eqnarray*}
\therefore ml\ddot{\theta}_1 + mg\sin\theta_1 - T_2\sin\left(\theta_2-\theta_1\right)=0
\end{eqnarray*}
この式に,$T_2$を代入すると次式となる.
\begin{eqnarray*}
ml\ddot{\theta}_1 + mg\sin\theta_1 - mg\cos\theta_2\sin\left(\theta_2-\theta_1\right) + ml\ddot{\theta}_1\sin^2\left(\theta_2-\theta_1\right)-ml\dot{\theta}_1^2\sin\left(\theta_2-\theta_1\right)\cos\left(\theta_2-\theta_1\right)-ml\dot{\theta}_2^2\sin\left(\theta_2-\theta_1\right) = 0
\end{eqnarray*}
よって,この系の運動方程式は次の2式となる.
\begin{eqnarray*}
&& ml\left\{1+\sin^2\left(\theta_2-\theta_1\right)\right\}\ddot{\theta}_1 + mg\sin\theta_1 - mg\cos\theta_2\sin\left(\theta_2-\theta_1\right) - ml\dot{\theta}_1^2\sin\left(\theta_2-\theta_1\right)\cos\left(\theta_2-\theta_1\right)-ml\dot{\theta}_2^2\sin\left(\theta_2-\theta_1\right) = 0 \\
&& ml\left\{\ddot{\theta}_1\cos\left(\theta_2-\theta_1\right)+ \dot{\theta}_1^2\sin\left(\theta_2-\theta_1\right) + \ddot{\theta}_2\ \right\} + mg\sin\theta_2 = 0
\end{eqnarray*}
3.2 固有角振動数と固有モード
微小振動を仮定して,固有角振動数と固有モードを求める.微小振動の場合,
\begin{eqnarray*}
\theta_1\ll 1\text{,}\theta_2\ll 1\text{, }\left|\theta_2-\theta_1\right|\ll1\text{, }\dot{\theta}_1\ll1\text{, }\dot{\theta}_2\ll1
\end{eqnarray*}
より,
\begin{eqnarray*}
&& \sin\theta_j\simeq\theta_j \left(j=1\text{, }2\right) \\
&& \cos\theta_j\simeq 1 \left(j=1\text{, }2\right) \\
&& \dot{\theta}_j^2 \simeq 0 \left(j=1\text{, }2\right)\\
&& \sin\left(\theta_2-\theta_1\right)\simeq\theta_2-\theta_1 \\
&& \cos\left(\theta_2-\theta_1\right)\simeq 1
\end{eqnarray*}
となるので,運動方程式は次式となる.
\begin{eqnarray*}
\left.\begin{array}{l}
ml\ddot{\theta}_1 + mg\theta_1 - mg\left(\theta_2-\theta_1\right) = 0 \\
ml\left(\ddot{\theta}_1 + \ddot{\theta}_2\ \right) + mg\theta_2 = 0
\end{array}\right\}
\end{eqnarray*}
第2式から第1式を引くと
\begin{eqnarray*}
ml\ddot{\theta}_2 + 2mg\left(\theta_2-\theta_1\right) = 0
\end{eqnarray*}
よって,第1式とこの式で次のような運動方程式を得る.
\begin{eqnarray*}
\left.\begin{array}{l}
\ddot{\theta}_1 + \frac{2g}{l}\theta_1 - \frac{g}{l}\theta_2 = 0 \\
\ddot{\theta}_2 - \frac{2g}{l}\theta_1 + \frac{g}{l}\theta_2 = 0
\end{array}\right\}
\end{eqnarray*}
定数係数の線形連立常微分方程式であり,特性根は純虚数となるので,$\Theta_j\left(j=1\text{, }2\right)$を未定係数として
\begin{eqnarray*}
\theta_j=\Theta_je^{ipt}
\end{eqnarray*}
とおいて,$p$に関する振動方程式を求める.即ち,
\begin{eqnarray*}
\left.\begin{array}{l}
\left(-p^2+\frac{2g}{l}\right)\Theta_1 - \frac{g}{l}\Theta_2 = 0 \\
- \frac{2g}{l}\Theta_1 + \left(-p^2+\frac{2g}{l}\right)\Theta_2 = 0
\end{array}\right\}
\end{eqnarray*}
行列表示すると
\begin{eqnarray*}
\left[\begin{array}{cc}
-p^2+\frac{2g}{l} & - \frac{g}{l} \\
- \frac{2g}{l} & -p^2+\frac{2g}{l}
\end{array}\right]\left[\begin{array}{c}
\Theta_1\\ \Theta_2
\end{array}\right]=
\left[\begin{array}{c}
0 \\ 0
\end{array}\right]
\end{eqnarray*}
よって,$\Theta_1$,$\Theta_2$が無意味な解を持たない条件
\begin{eqnarray*}
\left|\begin{array}{cc}
-p^2+\frac{2g}{l} & - \frac{g}{l} \\
- \frac{2g}{l} & -p^2+\frac{2g}{l}
\end{array}\right|=0
\end{eqnarray*}
が振動数方程式となる.よって,
\begin{eqnarray*}
\left(p^2-\frac{2g}{l}\right)^2 - 2\left(\frac{g}{l}\right)^2=0
\end{eqnarray*}
\begin{eqnarray*}
\therefore \left(p^2-\frac{2g}{l}+\sqrt{2}\frac{g}{l}\right)\left(p^2-\frac{2g}{l}-\sqrt{2}\frac{g}{l}\right)=0
\end{eqnarray*}
よって,
\begin{eqnarray*}
p^2=\frac{g}{l}\left(2\mp \sqrt{2}\right)
\end{eqnarray*}
即ち,符号のマイナス,プラスの順に第1次,第2次の固有角振動数となる.
\begin{eqnarray*}
\left.\begin{array}{l}
p_1\\
p_2
\end{array}\right\}=\sqrt{\frac{g}{l}\left(2\mp \sqrt{2}\right)}
\end{eqnarray*}
また,元の式に$p_j^2\left(j=1\text{, }2\right)$を代入すると次のような振幅比が定まる.
\begin{eqnarray*}
\left.
\frac{\Theta_2}{\Theta_1}
\right|_j = 2 - \frac{l}{g}p_j^2 =\left\{\begin{array}{cc}
\sqrt{2} & j=1 \\
-\sqrt{2} & j=2
\end{array}\right.
\end{eqnarray*}
よって,この系を固有な角振動数$p_1$,$p_2$で振動させると,$\theta_1$,$\theta_2$の振幅比が$\sqrt{2}$,$-\sqrt{2}$倍の振動をすることになる.即ち,1次モードで振動する場合
\begin{eqnarray*}
\left.\begin{array}{l}
\theta_1 =\alpha_1e^{ip_1t} \\
\theta_2=\sqrt{2}\alpha_1e^{ip_1t}
\end{array}\right\}
\end{eqnarray*}
一方,2次モードで振動する場合は,
\begin{eqnarray*}
\left.\begin{array}{l}
\theta_1 =\alpha_e^{ip_2t} \\
\theta_2=-\sqrt{2}\alpha_2e^{ip_2t}
\end{array}\right\}
\end{eqnarray*}
となる.1次モード,2次モードのイメージを示すと,図3-3のようになる.図3-3(a)に示す1次モードは,単振子と同様な振動をするのに対し,図3-3(b)の2次モードは2つの質点の振幅の符号が異なる,即ち,位相が180度ずれて振動することになる.
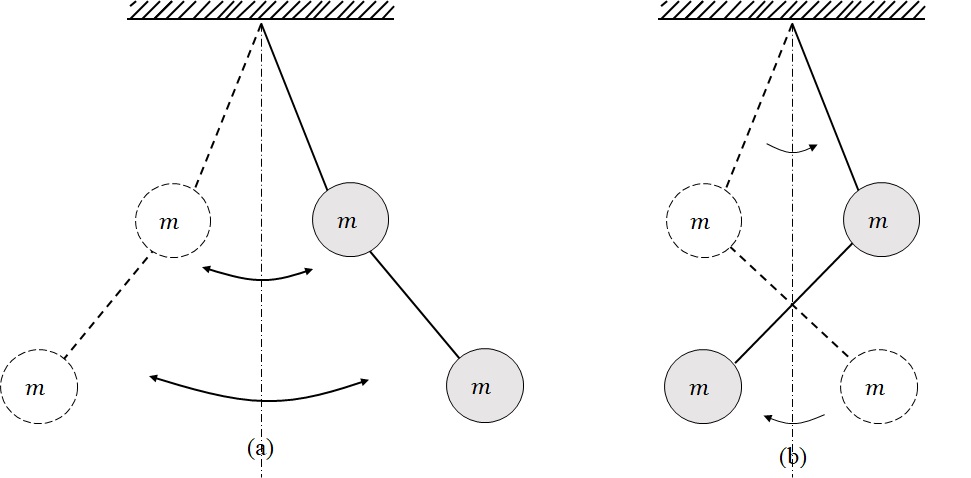
図3‐3 固有モードに対応する振幅比の分布イメージ
3.3 1自由度系との比較
2重振り子を1自由度系でモデル化することを考える.この場合,2つの質点が重心にあるとすると重心位置は支点から$\frac{3}{2}l$となり,この位置に$2m$の質量を集中させればよい.支点回りの慣性モーメント$I_O$は,2重振り子のままでも計算できるので計算すると
\begin{eqnarray*}
I_O=ml^2+m\left(2l\right)^2=5ml^2
\end{eqnarray*}
よって,支点回りの回転運動として運動方程式を立てると次のようになる.
\begin{eqnarray*}
I_O\ddot{\theta}+\frac{3l}{2}\sin\theta\times\left(2m\right)g =0
\end{eqnarray*}
よって,
\begin{eqnarray*}
5ml^2\ddot{\theta}+3mgl\sin\theta =0
\end{eqnarray*}
\begin{eqnarray*}
\therefore \ddot{\theta}+\frac{3g}{5l}\sin\theta =0
\end{eqnarray*}
微小振動を仮定すると
\begin{eqnarray*}
\therefore \ddot{\theta}+\frac{3g}{5l}\theta =0
\end{eqnarray*}
よって,この場合の固有角振動数は,
\begin{eqnarray*}
p=\sqrt{\frac{3g}{5l}}=\sqrt{\frac{g}{l}}\sqrt{0.6}
\end{eqnarray*}
となる.2重振り子の1次モードは
\begin{eqnarray*}
p_1=\sqrt{\frac{g}{l}\left(2-\sqrt{2}\right)}\simeq \sqrt{\frac{g}{l}}\sqrt{0.586}
\end{eqnarray*}
であるので,ある程度の近似が成り立つ.
3.4 演習
(1) 図3-4に示すようにそれぞれ質量$m_1$,$m_2$,長さ$l_1$,$l_2$の2つの単振子が支点から$h$の位置でばね定数$k$のばねで連結されている連結振り子を考える.2つの質量に対する運動方程式を求めよ.
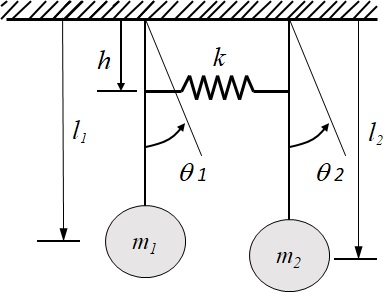
図3-4 連結振子の振動
(2)ばねに連結され水平方向に自由に移動できる質量$M$の台車に,図3-5に示すように質量$m$,長さ$l$の単振子が連結されている.台車の重心の水平方向位置を$x$,重心を原点として鉛直下向きに$z$軸を取り,その軸を基準とした単振子の回転角変位を反時計回りを正として$\theta$とする.$x$,$\theta$,共必ずしも微小で無いとして運動方程式を求める.
1) 単振子の絶対変位の$(x,z)$成分を与えられた記号を用いて示せ.
2) 単振子に発生する張力を$T$として,台車の$x$方向と単振子の$x$,$z$方向の運動方程式を示せ.
3) (1)の関係を用いて,$z$,張力$T$を消去し,$x$,$\theta$に対する運動方程式を求めよ.
4) 回転角変位が微小とした場合の運動方程式を求めよ.
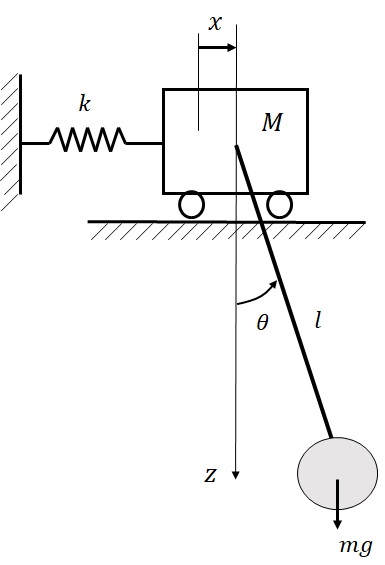
図3-5 クレーンモデルの振動





