4.回転と並進を伴う2自由度振動系
機械システムの運動は,一般に回転運動を伴いながら並進運動をしたり,並進運動している最中に回転動作をすることが多々存在する.ここでは,並進運動と回転運動を各1個ずつ考えた場合の振動問題について考える.
4.1 ばね支持された剛体の振動
乗用車の上下振動において,重心の運動だけでなく,前輪部,後輪部などの位置における変動まで調べたい場合には,車体に大きさを持たせ,重心の上下運動と重心回りの回転運動の2つを考えることにより,ある程度の事は調べることができる.
図4-1は,乗用車を真横から見た場合のモデルで,車体全体の質量を$m$,重心回りの慣性モーメントを$J$とし,重心位置がGで,重心位置から前後輪接地点までの水平方向距離をそれぞれ$l_1$,$l_2$しており,前後輪接地点で車体を支えているサスペンションに対応するばねのばね定数をそれぞれ$k_1$,$k_2$とおいたモデルである.この系に対する運動方程式を導出し,具体的な固有振動数と固有モードを計算し,振動特性について調べる.各モデルパラメータ値として,実際の普通自動車の値を想定して,$m=1600$kg, $J=mR^2=2304$kg$\cdot$m$^2$, $l_1=1.3$m, $l_2=1.7$m, $k_1=3.92\times10^4$N/m, $k_2=4.41\times10^4$N/mとして,実際に計算を行う.
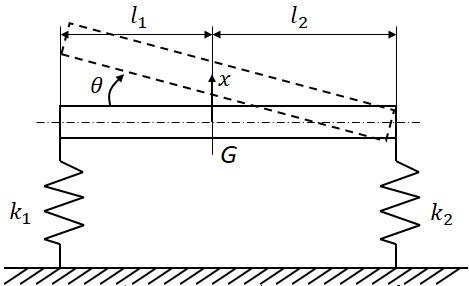
図4-1 乗用車の上下-ピッチ運動モデル
4.2 系の運動方程式
車体は重心Gが$x$上側に変位し,重心を中心に時計回りに$\theta$回転するとし,前後輪ばねには,引張力が発生しているとすると,この系に対するFree-body Diagramは,図4-2のようになる.前後輪部のばねの伸び$\Delta_1$,$\Delta_2$は,微小変形を仮定すると,$\sin\theta\simeq\tan\theta\simeq\theta$とおくことができるので,それぞれ
\begin{eqnarray*}
&& \Delta_1=x+l_1\sin\theta = x+l_1\tan\theta \simeq x + l_1\theta \\
&& \Delta_2=x-l_2\sin\theta = x-l_2\tan\theta \simeq x - l_2\theta
\end{eqnarray*}
となる.即ち,前後輪ばね部に発生する引張力$f_1$,$f_2$はそれぞれ
\begin{eqnarray*}
&& f_1= k_1\Delta_1 = k_1\left(x + l_1\theta\right) \\
&& f_2= k_2\Delta_2 = k_2\left(x - l_2\theta\right)
\end{eqnarray*}
と表現できる.これらの力によって発生する重心回りのモーメント$M_G$は時計回りを正とすると
\begin{eqnarray*}
M_G =-l_1\cos\theta\times f_1 + l_2\cos\theta\times f_2
\end{eqnarray*}
微小変形を仮定すると$\cos\theta\simeq1$なので,
\begin{eqnarray*}
M_G \simeq -l_1\times f_1 + l_2\times f_2
\end{eqnarray*}
重力による重心回りのモーメントは零となるので,回転運動を決めるモーメントは$M_G$のみとなる.よって,微小振動を仮定した場合の車体の並進運動と重心回りの回転運動に対する運動方程式は次のようになる.
\begin{eqnarray*}
&& m\ddot{x} = -f_1 - f_2 -mg = -k_1\Delta_1 -k_2\Delta_2 - mg = -k_1\left(x + l_1\theta\right)-k_2\left(x - l_2\theta\right) - mg \\
&& J\ddot{\theta} = M_G = -l_1\times f_1 + l_2\times f_2 = -l_1\times k_1\left(x + l_1\theta\right)+l_2\times k_2\left(x - l_2\theta\right)
\end{eqnarray*}
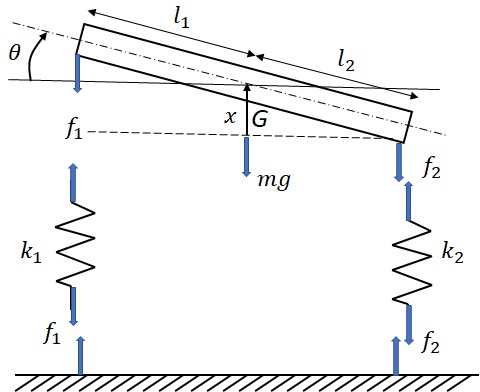
図4‐2 乗用車の上下-ピッチ運動モデルに対するFree-body Diagram
整理すると,この系の運動方程式は次式のようになる.
\begin{eqnarray*}
&& m\ddot{x} + \left(k_1+k_2\right)x + \left(k_1l_1-k_2l_2\right)\theta= -mg \\
&& J\ddot{\theta} + \left(k_1l_1-k_2l_2\right)x + \left(k_1l_1^2+k_2l_2^2\right)\theta=0
\end{eqnarray*}
この方程式において,静的な釣り合い状態を考えると,$\ddot{x}=0$,$\ddot{\theta}=0$であり,変位と回転は,$x=x_0$,$\theta=\theta_0$なる一定値とおけるので,
\begin{eqnarray*}
&& \left(k_1+k_2\right)x_0 + \left(k_1l_1-k_2l_2\right)\theta_0 = -mg \\
&& \left(k_1l_1-k_2l_2\right)x_0 + \left(k_1l_1^2+k_2l_2^2\right)\theta_0 = 0
\end{eqnarray*}
よって,$x$,$\theta$の原点をずらし,$x+x_0$,$\theta+\theta_0$で表現できる新たな変数$x$,$\theta$を取ると運動方程式は次のようになる.
\begin{eqnarray*}
&& \quad \left.\begin{array}{l}
m\ddot{x} + \left(k_1+k_2\right)\left(x+x_0\right) + \left(k_1l_1-k_2l_2\right)\left(\theta+\theta_0\right) = -mg \\
J\ddot{\theta} + \left(k_1l_1-k_2l_2\right)\left(x+x_0\right) + \left(k_1l_1^2+k_2l_2^2\right)\left(\theta+\theta_0\right)=0
\end{array}\right\} \\
&& \therefore \left.\begin{array}{l}
m\ddot{x} + \left(k_1+k_2\right)x + \left(k_1l_1-k_2l_2\right)\theta + \left(k_1+k_2\right)x_0 + \left(k_1l_1-k_2l_2\right)\theta_0 = -mg \\
J\ddot{\theta} + \left(k_1l_1-k_2l_2\right)x + \left(k_1l_1^2+k_2l_2^2\right)\theta + \left(k_1l_1-k_2l_2\right)x_0 + \left(k_1l_1^2+k_2l_2^2\right)\theta_0 = 0
\end{array}\right\} \\
\end{eqnarray*}
よって,静的な釣り合い状態からの運動を考える場合には,静的な釣り合い状態の関係を使って,次のような運動方程式とすることができる.
\begin{eqnarray*}
&& m\ddot{x} + \left(k_1+k_2\right)x + \left(k_1l_1-k_2l_2\right)\theta= 0 \\
&& J\ddot{\theta} + \left(k_1l_1-k_2l_2\right)x + \left(k_1l_1^2+k_2l_2^2\right)\theta=0
\end{eqnarray*}
このように,重力方向と同じ方向の重心の並進運動,重心回りの回転運動を考え,静的な釣り合い状態を原点とする並進,回転変位を考えることにより,重力をキャンセルした形の運動方程式を求めることができる.
4.3 固有振動数と固有モード
得られた運動方程式をそれぞれ$m$,$J$で割ると
\begin{eqnarray*}
&& \ddot{x} + \frac{k_1+k_2}{m}x + \frac{k_1l_1-k_2l_2}{m}\theta=0\\
&& \ddot{\theta} + \frac{k_1l_1-k_2l_2}{J}x + \frac{k_1l_1^2+k_2l_2^2}{J}\theta=0
\end{eqnarray*}
未定係数をそれぞれ$X$,$\Theta$,$p$を角振動数として解を次式とおく.
\begin{eqnarray*}
&& x=Xe^{ipt} \\
&& \theta=\Theta e^{ipt}
\end{eqnarray*}
運動方程式に代入し,整理すると次式を得る.
\begin{eqnarray*}
&& \left(-p^2 + \frac{k_1+k_2}{m}\right)X + \frac{k_1l_1-k_2l_2}{m}\Theta=0\\
&& \frac{k_1l_1-k_2l_2}{J}X + \left(-p^2+\frac{k_1l_1^2+k_2l_2^2}{J}\right)\Theta = 0
\end{eqnarray*}
この式を行列形式で表すと
\begin{eqnarray*}
\left[\begin{array}{cc}
-p^2 + \frac{k_1+k_2}{m} & \frac{k_1l_1-k_2l_2}{m}\\
\frac{k_1l_1-k_2l_2}{J} & -p^2+\frac{k_1l_1^2+k_2l_2^2}{J}
\end{array}\right]\left[\begin{array}{c}
X \\ \Theta
\end{array}\right]=\left[\begin{array}{c}
0 \\ 0
\end{array}\right]
\end{eqnarray*}
よって,$X$,$\Theta$が共に零にはならない解が存在するためには,左辺の係数行列について次の関係が成り立つ必要がある.
\begin{eqnarray*}
\left|\begin{array}{cc}
-p^2 + \frac{k_1+k_2}{m} & \frac{k_1l_1-k_2l_2}{m}\\
\frac{k_1l_1-k_2l_2}{J} & -p^2+\frac{k_1l_1^2+k_2l_2^2}{J}
\end{array}\right| = \left(-p^2 + \frac{k_1+k_2}{m}\right)\left(-p^2+\frac{k_1l_1^2+k_2l_2^2}{J}\right) - \left(\frac{k_1l_1-k_2l_2}{m}\right)\left(\frac{k_1l_1-k_2l_2}{J}\right)= 0
\end{eqnarray*}
即ち,次の角振動数$p$に関する4次方程式が定まる.
\begin{eqnarray*}
p^4 - \left(\frac{k_1+k_2}{m}+\frac{k_1l_1^2+k_2l_2^2}{J}\right)p^2 + \frac{\left(k_1+k_2\right)\left(k_1l_1^2+k_2l_2^2\right)}{mJ}- \frac{\left(k_1l_1-k_2l_2\right)^2}{mJ}= 0
\end{eqnarray*}
この方程式は$p^2$の2次方程式であるので,解の性質について考える.判別式$D$は,
\begin{eqnarray*}
D=\left(\frac{k_1+k_2}{m}+\frac{k_1l_1^2+k_2l_2^2}{J}\right)^2-\frac{4\left(k_1+k_2\right)\left(k_1l_1^2+k_2l_2^2\right)}{mJ}+ \frac{4\left(k_1l_1-k_2l_2\right)^2}{mJ}=\left(\frac{k_1+k_2}{m}-\frac{k_1l_1^2+k_2l_2^2}{J}\right)^2 + \frac{4\left(k_1l_1-k_2l_2\right)^2}{mJ}\geq 0
\end{eqnarray*}
となるので,$p^2$は,2つの実根となる.また,元の方程式の定数部は
\begin{eqnarray*}
\frac{\left(k_1+k_2\right)\left(k_1l_1^2+k_2l_2^2\right)}{mJ}- \frac{\left(k_1l_1-k_2l_2\right)^2}{mJ}= \frac{k_1k_2\left(l_1+l_2\right)^2}{mJ} > 0
\end{eqnarray*}
となるので,
\begin{eqnarray*}
\left(\frac{k_1+k_2}{m}+\frac{k_1l_1^2+k_2l_2^2}{J}\right)^2 > D = \left(\frac{k_1+k_2}{m}+\frac{k_1l_1^2+k_2l_2^2}{J}\right)^2-\frac{4k_1k_2\left(l_1+l_2\right)^2}{mJ}
\end{eqnarray*}
より,
\begin{eqnarray*}
\frac{k_1+k_2}{m}+\frac{k_1l_1^2+k_2l_2^2}{J} > \sqrt{D}
\end{eqnarray*}
よって,$p^2$は正の値をとるので,値の小さい方から順に$p_1$,$p_2$とすると,固有角振動数は次式により定まることになる.
\begin{eqnarray*}
\left.\begin{array}{l}
p_1^2 \\ p_2^2
\end{array}\right\}= \frac{1}{2}\left[\frac{k_1+k_2}{m}+\frac{k_1l_1^2+k_2l_2^2}{J} \mp \sqrt{D}\right]
\end{eqnarray*}
また,この場合の振幅比は,運動方程式第1式を使うと
\begin{eqnarray*}
&& \left(-p^2 + \frac{k_1+k_2}{m}\right)X + \frac{k_1l_1-k_2l_2}{m}\Theta=0\\
&& \therefore \frac{X}{\Theta}=\frac{k_1l_1-k_2l_2}{k_1+k_2-mp^2}
\end{eqnarray*}
となるので,2つの固有角振動数$p_j(j=1,2)$に対して,振動モードに対応する2つの振幅比が次式で定まることになる.
\begin{eqnarray*}
\left.\frac{X}{\Theta}\right|_j=\frac{k_1l_1-k_2l_2}{k_1+k_2-mp_j^2}\equiv \lambda_j
\end{eqnarray*}
数値を代入して,固有角振動数を計算すると
\begin{eqnarray*}
&& p_1\fallingdotseq 6.91\text{rad/s}\\
&& p_2\fallingdotseq 9.401\text{rad/s}
\end{eqnarray*}
となるので,第1次と第2次の固有振動数は,次の値となる.
\begin{eqnarray*}
f_1\fallingdotseq 1.10\text{Hz}\\
f_2\fallingdotseq 1.50\text{Hz}
\end{eqnarray*}
また,振幅比は
\begin{eqnarray*}
&& \lambda_1\fallingdotseq 3.472 \text{m}\\
&& \lambda_2\fallingdotseq -0.413 \text{m}
\end{eqnarray*}
となる.ここで,
\begin{eqnarray*}
\left.\begin{array}{l}
x=X_je^{ip_jt} \\
\theta=\Theta_je^{ip_jt}
\end{array}\right\}
\end{eqnarray*}
において,重心Gの上下方向振幅$X_j$に対し,重心回りに$\Theta_j$回転させることにより,振幅$X_j$,$\Theta_j$,$\lambda_j$の位置関係を考える.ここで,$\lambda_2$は負符号であるので,回転を逆方向に回転させることにすると図4-3のような位置関係を定めることができる.定められた振幅比$\lambda_j(j=1,2)$は,各モードにおいて車体(あるいはそれを水平方向に延長した線上)の振動振幅が零となる点$D_j(j=1,2)$を示す位置に対応している.並進運動と回転運動を伴う剛体の運動は,瞬間中心回りの回転運動だけで表現できるが,固有振動が発生する場合においては,振幅比$\lambda_j$で定まる点$D_j$を中心とした回転振動で振動する,即ち,この系は,固有振動数$f_j$で振動する場合,振幅比$\lambda_j$で定まる点$D_j$を中心とした回転振動モードが現れることがわかる.

図4-3 乗用車の上下-ピッチ運動に対する2つの振動モード
4.4 集中質量系の並進・回転運動モデル
質量が一様に分布している(と考えた)剛体に対して,重心位置ではなく,他の位置に質量を振り分けて(分布させて)考える振動も考えられる.図4-4は,全体の長さが$l$で,質量が無視できる剛体棒の両端に$m$の質量が集中していると考えた物体に対して,左端の質量を配した箇所と距離$l$離れた全体の中心位置をばね定数$k$のばねで支持した系を表しており,このモデルにより,上下並進運動と面内の回転運動を考えることができる.
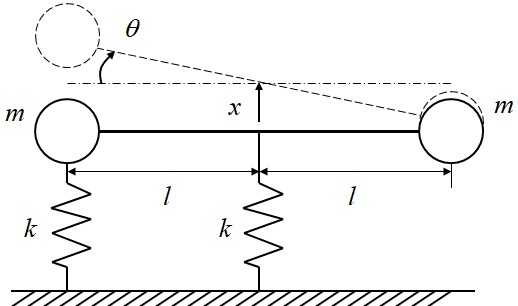
図4-4 上下-ピッチ運動集中質量系モデル
この場合,全体の質量は$2m$で重心位置は,ばねで支持されている中心位置である.また,重心回りの慣性モーメントは,$2\times ml^2$となる.各質量に対する運動を考えるのでなく,質量$2m$,重心回りの慣性モーメントが$2ml^2$の物体の運動として,運動方程式を考えることにする.ばねで支持されている左端の質量部分と中央部に作用する力について,ばねに引張力が働くとするとFree-body Diagramは,図4-5のようになる.

図4-5 上下-ピッチ運動集中質量系モデルに対するFree-body Diagram
静的な釣り合い状態を原点とする上下方向変位を$x$,回転角変位を$\theta$として,重力項の影響を考える必要が無いので,物体に作用する力は図に示すようなばね力のみとなる.ここで,微小変形を仮定すると,左端の変位は,$x+l\theta$となるので,左側のばねの伸びは$\Delta_1=x+l\theta$となる.中心部は変位$x$なので,ばね伸び変位は,$\Delta_2=x$である.よって,図に示すばね力$f_1$,$f_2$は次のようになる.
\begin{eqnarray*}
&& f_1=k\left(x+l\theta\right) \\
&& f_2=kx
\end{eqnarray*}
また,重心回りのモーメントは,$M_O=-l\times f_1$のみとなるので,この系の重心の上下方向運動と重心回りの回転運動に対する運動方程式は次のようになる.
\begin{eqnarray*}
&& 2m\ddot{x} = -f_1-f_2 = -k\left(x+l\theta\right)-kx \\
&& 2ml^2\ddot{\theta} = M_O = -l\times f_1 = -kl\left(x+l\theta\right)
\end{eqnarray*}
整理すると系の運動方程式は次のようになる.
\begin{eqnarray*}
\left.\begin{array}{l}
2m\ddot{x} + 2kx + kl\theta =0\\
2ml^2\ddot{\theta} + klx + kl^2\theta=0
\end{array}\right\}
\end{eqnarray*}
剛体で考えた場合とほとんど同じであるので,この方程式を用いて,固有振動数と固有モードを計算し,系の固有モードについて考察してみると良い.
4.5 演習
1.図4-6に示すような系の上下並進運動と面内の回転運動に対する運動を考える.間隔$l$で,質量$m$の3つの物体をつないでいる棒の質量は無視でき,重心変位を$x$,重心回りの回転を$\theta$として,以下の問に答えなさい.
(1) 系の運動方程式を求めなさい.
(2) 系の固有角振動数を式で示しなさい.
(3) 系の固有モードについて説明しなさい.

図4-6 集中質量を配した系の上下-ピッチ振動モデル
2.図4-7に示すように,質量が無視できる長さ$4l$の棒の両端は,ばね定数$k$, $2k$のばねで支持されており,棒中央と右端にそれぞれ質量$m$の物体が配置されているとする.重心変位を$x$,重心回りの回転を$\theta$として,以下の問に答えなさい.
(1) 系の運動方程式を求めなさい.
(2) 系の固有角振動数を式で示しなさい.
(3) 系の固有モードについて説明しなさい.
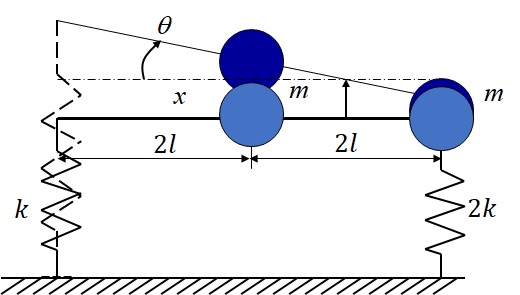
図4-7 2つの集中質量を持つ櫛状物体の上下-ピッチ振動モデル







