5.2自由度振動系の力による強制振動
機械力学Ⅰで学んだように,一般の機械システムは共振振動数を持ち,運転時の回転や往復運動に伴う周期的な変動荷重や外部から加わる振動的な力により,振動が極端に大きくなる現象を生じることがある.ここでは,自由度が2つに増えた2自由度振動系に周期的な入力が加わった場合の挙動について調べる.
5.1 例題
質量$m$の二つの物体A,Bがばね定数$k$の3個のばねでなめらかな水平面上に図5-1のように連結されている.いまAに強制外力$P\cos\omega t$が作用するときA,Bの強制振動の式を導き,かつ応答曲線を図で示すことにする.
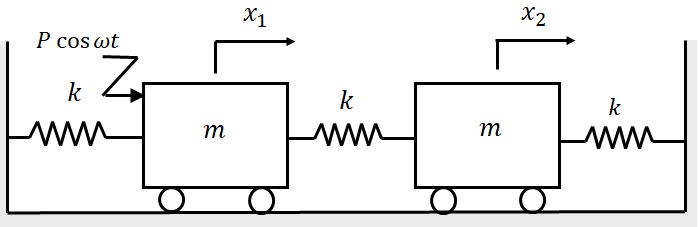
図5-1 2自由度振動系強制振動モデルの例
5.2 系の運動方程式
この系のFree-body Diagramは,図5-2のようになる.各ばねに発生する力$f_1$,$f_2$,$f_3$は,ばねが伸びると仮定すると
\begin{eqnarray*}
\left. \begin{array}{l}
f_1=k\left(x_1-0\right)=kx_1\\
f_2=k\left(x_2-x_1\right)\\
f_3=k\left(0-x_2\right)=-kx_2
\end{array}\right\}
\end{eqnarray*}
より運動方程式は次のようになる.
\begin{eqnarray*}
\left. \begin{array}{l}
m\ddot{x}_1 = -f_1 + f_2 + P\cos\omega t = -kx_1+k\left(x_2-x_1\right) + P\cos\omega t\\
m\ddot{x}_2 = - f_2 + f_3 = -k\left(x_2-x_1\right) - kx_2
\end{array}\right\}
\end{eqnarray*}
整理すると,次式を得る.
\begin{eqnarray*}
\left. \begin{array}{l}
m\ddot{x}_1 + 2kx_1 - kx_2 = P\cos\omega t\\
m\ddot{x}_2 - kx_1 + +2kx_2= 0
\end{array}\right\}
\end{eqnarray*}
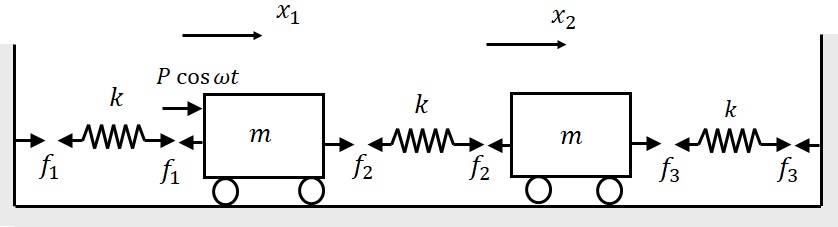
図5-2 2自由度振動系強制振動モデルのFree-body Diagram
5.3 振幅特性
強制振動応答は共に
\begin{eqnarray*}
x_j=X_j\cos\omega t + Y_j\sin\omega t (j=1,\quad 2)
\end{eqnarray*}
の形となるが,右辺が$\cos\omega t$なので$Y_j=0$は自明となる.よって,運動方程式を代入すると
\begin{eqnarray*}
\left. \begin{array}{l}
\left\{\left(-m\omega^2+2k\right\}X_1 -k X_2 - P\right\}\cos\omega t=0\\
\left\{-kX_1 + \left(-m\omega^2 +2k\right)X_2\right\}\cos\omega t= 0
\end{array}\right\}
\end{eqnarray*}
よって,$X_1$,$X_2$に関する2次方程式となるので,行列形式で表示すると次式となる.
\begin{eqnarray*}
\left[\begin{array}{cc}
2k-m\omega^2 & -k \\
-k & 2k-m\omega^2
\end{array}\right]\left[\begin{array}{c}
X_1 \\ X_2
\end{array}\right]=\left[\begin{array}{c}
P \\ 0
\end{array}\right]
\end{eqnarray*}
左から係数行列の逆行列をかける.
\begin{eqnarray*}
\left[\begin{array}{c}
X_1 \\ X_2
\end{array}\right] &=&
\frac{1}{\left(2k-m\omega^2\right)^2-k^2}
\left[\begin{array}{cc}
2k-m\omega^2 & k \\
k & 2-m\omega^2
\end{array}\right]
\left[\begin{array}{c}
P \\ 0
\end{array}\right]\\
&=& \frac{P}{\left(k-m\omega^2\right)\left(3k-m\omega^2\right)}
\left[\begin{array}{c}
2k-m\omega^2 \\ k
\end{array}\right]\\
&=& \frac{P/m}{\left(\frac{k}{m}-\omega^2\right)\left(\frac{3k}{m}-\omega^2\right)}
\left[\begin{array}{c}
\frac{2k}{m}-\omega^2 \\ \frac{k}{m}
\end{array}\right]\\
\end{eqnarray*}
ここで,$p_1=\sqrt{\frac{k}{m}}$,$p_2=\sqrt{\frac{3k}{m}}$は,第1次,第2次の固有角振動数であり,
\begin{eqnarray*}
\left[\begin{array}{c}
X_1 \\ X_2
\end{array}\right]
= \frac{P/m}{\left(p_1^2-\omega^2\right)\left(p_2^2-\omega^2\right)}
\left[\begin{array}{c}
\frac{2k}{m}-\omega^2 \\ \frac{k}{m}
\end{array}\right]\\
\end{eqnarray*}
と書けるので,1自由度系の場合と同様,強制外力の角周波数$\omega$がどちらかの固有角振動数と同じ値を取るとき,振動振幅は無限大となることが分かる.$\delta_{st}=F/k$と置き,分母分子を$p_1^2$で割ると次式を得る.
\begin{eqnarray*}
\left[\begin{array}{c}
X_1 \\ X_2
\end{array}\right]
= \frac{\delta_{st}}{\left\{1-\left(\frac{\omega}{p_1}\right)^2\right\}\left\{3-\left(\frac{\omega}{p_1}\right)^2\right\}}
\left[\begin{array}{c}
2-\left(\frac{\omega}{p_1}\right)^2 \\ 1
\end{array}\right]
\end{eqnarray*}
横軸に$\frac{\omega}{p_1}$を取り,縦軸に,$X_1/\delta_{st}$,$X_2/\delta_{st}$を取ると,図5-3のような振幅特性を示すグラフが得られる.
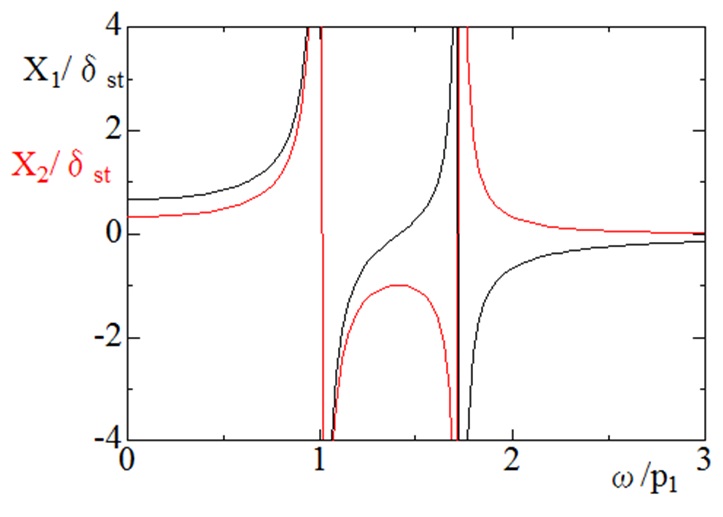
図5‐3 2自由度振動系の応答曲線
よって,物体A,Bの強制振動応答を時間の関数として表すと次式となる.
\begin{eqnarray*}
&& x_1=\frac{\delta_{st}\left\{2-\left(\frac{\omega}{p_1}\right)^2\right\}}{\left\{1-\left(\frac{\omega}{p_1}\right)^2\right\}\left\{3-\left(\frac{\omega}{p_1}\right)^2\right\}}\cos\omega t \\
&& x_2=\frac{\delta_{st}}{\left\{1-\left(\frac{\omega}{p_1}\right)^2\right\}\left\{3-\left(\frac{\omega}{p_1}\right)^2\right\}}\cos\omega t
\end{eqnarray*}
ここで,$\cos\omega t$の係数は一般的には,”振幅”と呼ばれるが,この記述だと$\omega$の値に応じて符号を変える.そこで,一般的な周期的な振動で記述される”振幅”と”位相”を用いた次式のような定式化を行うと”振幅”は大きさのみを表し,振幅特性がより分かり易くなる(かもしれない).
\begin{eqnarray*}
&& x_1=\left|\frac{\delta_{st}\left\{2-\left(\frac{\omega}{p_1}\right)^2\right\}}{\left\{1-\left(\frac{\omega}{p_1}\right)^2\right\}\left\{3-\left(\frac{\omega}{p_1}\right)^2\right\}}\right|\cos\left(\omega t-\phi_1\right) \\
&& x_2=\left|\frac{\delta_{st}}{\left\{1-\left(\frac{\omega}{p_1}\right)^2\right\}\left\{3-\left(\frac{\omega}{p_1}\right)^2\right\}}\right|\cos\left(\omega t - \phi_2\right)
\end{eqnarray*}
ここに示す振幅特性は,図5-4の上図のようになる.また,ここで示した位相$\phi_1$,$\phi_2$は下図のように"0"rad(零度)から"$\pi$"rad(180度)を行ったり来たりすることになる.固有モードでは,1次モードが同位相,2次モードは逆位相となっていたが,強制入力が加わる場合は,第1次の固有振動数前後の振動数で加振されている場合は2つの物体は同位相で振動し,第2次の固有振動数前後では逆位相で振動することが分かる.また,入力が加えられている側の物体には,全く振動しない点(零点,ここでは,$\frac{\omega}{p_1}=\sqrt{2}$)が存在することが分かる.
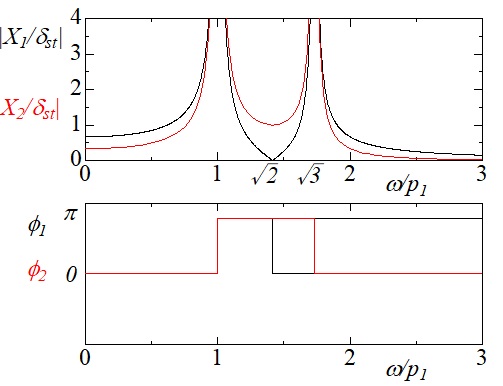
図5‐4 2自由度振動系の強制振動における応答振幅と位相
5.4 結果の整理
質量,ばね共異なる図5-5に示す2自由度振動系の強制振動に関する結果をまとめておく.運動方程式は,
\begin{eqnarray*}
&& m_1\ddot{x}_1+\left(k_1+k_2\right)x_1 -k_2x_2= P\cos\omega t \\
&& m_2\ddot{x}_2 - k_2x_1 + \left(k_2+k_3\right)x_2 = 0
\end{eqnarray*}
強制振動に対する応答は,$x_j=X_j\cos\omega t$となるので,これを方程式に代入すると次式を得る.
\begin{eqnarray*}
\left. \begin{array}{l}
\left(-m_1\omega^2+k_1+k_2\right\}X_1 -k_2 X_2 = P\\
-k_2X_1 + \left(-m_2\omega^2 +k_2+k_3\right)X_2= 0
\end{array}\right\}
\end{eqnarray*}
行列形式で表示すると,
\begin{eqnarray*}
\left[\begin{array}{cc}
k_1+k_2-m_1\omega^2 & -k_2 \\
-k_2 & k_2+k_3-m_2\omega^2
\end{array}\right]\left[\begin{array}{c}
X_1 \\ X_2
\end{array}\right]=\left[\begin{array}{c}
P \\ 0
\end{array}\right]
\end{eqnarray*}
\begin{eqnarray*}
\therefore \left[\begin{array}{c}
X_1 \\ X_2
\end{array}\right]=\frac{1}{\Delta}
\left[\begin{array}{cc}
k_2+k_3-m_1\omega^2 & k_2 \\
k_2 & k_1+k_2-m_2\omega^2
\end{array}\right]
\left[\begin{array}{c}
P \\ 0
\end{array}\right]
\end{eqnarray*}
ここで,
\begin{eqnarray*}
\Delta =\left(k_1+k_2-m_1\omega^2\right)\left(k_2+k_3-m_2\omega^2\right)-k_2^2
\end{eqnarray*}
であり,$\Delta =0$は振動数方程式であり,これを解くと,この系の固有角振動数が2組定まる.これらを$p_1$,$p_2$とすると,
\begin{eqnarray*}
\Delta =m_1m_2\left(p_1^2-\omega^2\right)\left(p_2^2-\omega^2\right)
\end{eqnarray*}
とおけるので,応答振幅は次式となる.
\begin{eqnarray*}
\therefore \left[\begin{array}{c}
X_1 \\ X_2
\end{array}\right]
=\frac{P/m_1}{\left(\omega^2-p_1^2\right)\left(\omega^2-p_2^2\right)}
\left[\begin{array}{c}
\frac{k_2+k_3}{m_2}-\omega^2 \\
\frac{k_2}{m_2}
\end{array}\right]
\end{eqnarray*}
ここで,
\begin{eqnarray*}
p^2 = \frac{k_1}{m_1}\text{, }p_a^2=\frac{k_2}{m_2}\text{, } \delta_{st}=P/k_1
\end{eqnarray*}
とおくと,
\begin{eqnarray*}
\therefore \left[\begin{array}{c}
X_1 \\ X_2
\end{array}\right]
=\frac{\delta_{st}}{\left\{\left(\frac{\omega}{p}\right)^2-\left(\frac{p_1}{p}\right)^2\right\}\left\{\left(\frac{\omega}{p}\right)^2-\left(\frac{p_2}{p}\right)\right\}}
\left[\begin{array}{c}
\left(\frac{p_a}{p}\right)^2+\frac{m_1}{m_2}\frac{k_2}{k_1}-\left(\frac{\omega}{p}\right)^2 \\
\frac{p_a}{p}
\end{array}\right]
\end{eqnarray*}
結果から分かるように,振幅$X_1$は,分母の符号が変わる2回と分子の符号が変わるで計3回符号が変わるのに対し,振幅$X_2$は,分母の符号が変化する2回のみの符号変化である.また,こ$x_1$は振幅が零となる角振動数が存在し,
\begin{eqnarray*}
\left(\frac{\omega}{p}\right)^2=\left(\frac{p_a}{p}\right)^2+\frac{m_1}{m_2}\frac{k_2}{k_1}
\end{eqnarray*}
の時である.式から分かるように,この値は質量やばね定数の変更により値を調整することが可能であることから,動吸振器などの設計において応用される関係である.質量$m_1$の物体の振動を零にしたい場合,質量$m_2$の物体の質量の大きさやばね定数をうまく調整すれば,$m_1$の物体の振動振幅を零とすることができる(はずである).

図5-5 2自由度振動系強制振動
5.5 演習
(1) 質量120㎏の機械が12Hzの振動数をもつ強制調和力を受け振動している.機械に5㎏の質量をばねで取り付け振動を停止させたい.ばね定数はいくらにするとよいか.
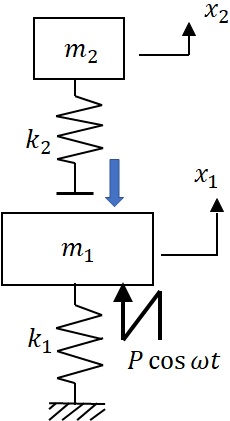
図5-6 2自由度振動系を利用した制振
(2) 図5-7は,質量$m_1$の台車がばね定数$k_1$のばねで壁に連結されており,台車上に設置された質量$m_2$の荷物がばね定数$k_2$のばねで台車と連結された系を表している.台車は地面に対して水平方向に滑らかに動くことができ,荷物もまた台車上を水平方向に滑らかに動くことができるとする.図に示すように$m_2$に強制外力を加える.定常応答振幅を与えられた記号を用いて示し,$m_1=10$[kg],$m_2=15$[kg],$k_1=1.75$[kN/m],$k_2=1.5$[kN/m]の系に対して,$P=10$Nとしたとき,$m_2$の応答振幅が最小となる角周波数$\omega$を求めよ.
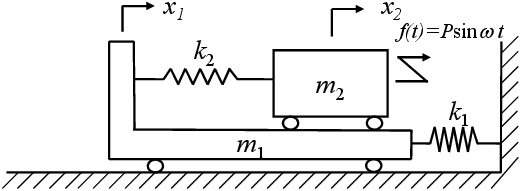
図5-7 2自由度振動系を強制振動







