6.2自由度系の変位による強制振動
ビデオ:”振動の世界”
6.1 例題:自動車走行時の上下方向振動
凹凸路面を走行する自動車の振動を調べるために,図6-1に示すように,凹凸路面の表面は,波長$\lambda$,振幅$a$で正弦的に変化する形状をしており自動車が走行しても路面形状が変化することは無い程剛であると仮定し,2自由度振動系の応答を考える.タイヤ,車軸等ばね下質量に対応する$m_1$をタイヤ剛性に対応するばね定数$k_1$のばねで路面上に接地し,サスペンション等に対応するばね定数$k_2$のばねで,車体等ばね上の質量に対応する$m_2$の質量を支えている系である.速度$v$で走行すると路面からの変位入力は,一波長$\lambda$で基準位置(零)から振幅$a$まで上がった後,基準基地に戻りさらに$-a$へまで下がった後,基準位置まで戻るという正弦的な変動を受ける.従って,図に示すように上下方向の加振角周波数を次式のように考えることができる.
\begin{eqnarray*}
\omega = \frac{2\pi v}{\lambda}
\end{eqnarray*}
よって,ばね定数$k_1$のばねの下端は,上下方向に
\begin{eqnarray*}
u = a\sin\omega t
\end{eqnarray*}
で”変位入力”を受けることになる.これらの式から,走行速度$v$を上げると自動車の路面からの加振角周波数は対応して上がって行くことが分かる.
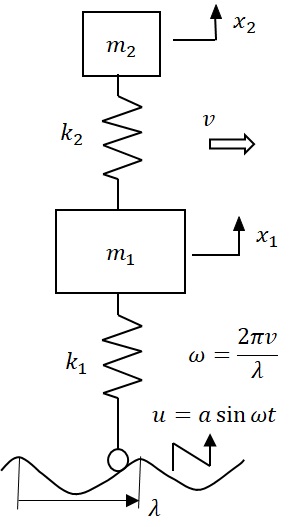
図6-1 路面上を走行する2自由度振動系モデル
図6-1に示すように各質量$m_1$,$m_2$の上下方変位をそれぞれ$x_1$,$x_2$とし,各ばねに引張力が発生している,と仮定すると,図6-2に示すようなFree-body Diagramを描くことができる.ばね定数$k_1$,$k_2$のばねの伸びはそれぞれ,
\begin{eqnarray*}
&& \Delta_1=x_1-u \\
&& \Delta_2=x_2-x_1
\end{eqnarray*}
であるので,ばねに発生する引張力$f_1$,$f_2$は次式となる.
\begin{eqnarray*}
&& f_1=k_1\Delta_1=k_1\left(x_1-u\right) \\
&& f_2=k_2\Delta_2=k_2\left(x_2-x_1\right)
\end{eqnarray*}
よって,2つの質量に対して,ニュートンの第2法則を適用すると次式となる.
\begin{eqnarray*}
&& m_1\ddot{x}_1 = -f_1+f_2 = -k_1\left(x_1-u\right)+k_2\left(x_2-x_1\right) \\
&& m_2\ddot{x}_2 = -f_2 = -k_2\left(x_2-x_1\right)
\end{eqnarray*}
$u=a\sin\omega t$を代入して整理すると,次の運動方程式となる.
\begin{eqnarray*}
&& m_1\ddot{x}_1 +\left(k_1+k_2\right)x_1- k_2x_2 = k_1a\sin\omega t \\
&& m_2\ddot{x}_2 - k_2x_1 + k_2x_2 =0
\end{eqnarray*}
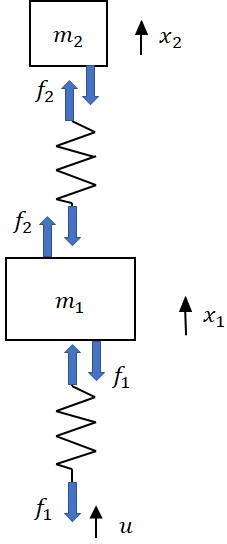
図6-2 路面上を走行する2自由度振動系モデルのFree-body Diagram
強制振動応答解を考えると,解は$x_j=X_j\sin\omega t(j=1,2)$とおけるので,代入して整理すると次式を得る.
\begin{eqnarray*}
&& \left(-m_1\omega^2+k_1+k_2\right)X_1- k_2X_2 = k_1a \\
&& -k_2X_1 + \left(-m_2\omega^2 + k_2\right)X_2 =0
\end{eqnarray*}
行列形式で表現し,不定係数$X_J(j=1,2)$を求める.
\begin{eqnarray*}
\left[\begin{array}{cc}
k_1+k_2-m_1\omega^2 & - k_2\\
-k_2 & k_2-m_2\omega^2
\end{array}\right]\left[\begin{array}{c}
X_1 \\ X_2
\end{array}\right] = \left[\begin{array}{c}
k_1a \\ 0
\end{array}\right]
\end{eqnarray*}
係数行列の逆行列を左からかけると次式を得る.
\begin{eqnarray*}
\left[\begin{array}{c}
X_1 \\ X_2
\end{array}\right] &=& \frac{1}{\left(k_1+k_2-m_1\omega^2\right)\left(k_2-m_2\omega^2\right)-k_2^2}
\left[\begin{array}{cc}
k_2-m_2\omega^2 & k_2\\
k_2 & k_1+k_2-m_1\omega^2
\end{array}\right]
\left[\begin{array}{c}
k_1a \\ 0
\end{array}\right]\\
&=& \frac{k_1a}{\left(k_1+k_2-m_1\omega^2\right)\left(k_2-m_2\omega^2\right)-k_2^2}
\left[\begin{array}{c}
k_2-m_2\omega^2 \\ k_2
\end{array}\right]
\end{eqnarray*}
ここで,上式の分母を零にする$\omega$,即ち,2つの固有角振動数を$p_1$,$p_2$とすると
\begin{eqnarray*}
\left[\begin{array}{c}
X_1 \\ X_2
\end{array}\right]
= \frac{k_1a/m_1}{\left(\omega^2-p_1^2\right)\left(\omega^2-p_2^2\right)}
\left[\begin{array}{c}
\frac{k_2}{m_2}-\omega^2 \\ \frac{k_2}{m_2}
\end{array}\right]
\end{eqnarray*}
但し
\begin{eqnarray*}
\left.\begin{array}{l}
p_1^2 \\ p_2^2 \end{array}\right\} = \frac{1}{2}\left\{\frac{k_1+k_2}{m_1}+\frac{k_2}{m_2}\mp\sqrt{\left(\frac{k_1+k_2}{m_1}+\frac{k_2}{m_2} \right)^2-\frac{4k_1k_2}{m_1m_2}} \right\}
\end{eqnarray*}
よって,この系の強制振動に対する応答は次式のようになる.
\begin{eqnarray*}
&& x_1= \frac{\frac{k_1}{m_1}\left(\frac{k_2}{m_2}-\omega^2\right)}{\left(p_1^2-\omega^2\right)\left(p_2^2-\omega^2\right)}a\sin\omega t \\
&& x_2= \frac{\frac{k_1}{m_1}\frac{k_2}{m_2}}{\left(p_1^2-\omega^2\right)\left(p_2^2-\omega^2\right)}a\sin\omega t
\end{eqnarray*}
振幅について更に,$p^2=k_1/m_1$,$p_a=k_2/m_2$と置くと次の形となる.
\begin{eqnarray*}
\left[\begin{array}{c}
X_1 \\ X_2
\end{array}\right]
= \frac{a}{\left\{\left(\frac{\omega}{p}\right)^2-\left(\frac{p_1}{p}\right)^2\right\}\left\{\left(\frac{\omega}{p}\right)^2-\left(\frac{p_2}{p}\right)^2\right\}}
\left[\begin{array}{c}
\left(\frac{p_a}{p}\right)^2-\left(\frac{\omega}{p}\right)^2 \\ \left(\frac{p_a}{p}\right)^2
\end{array}\right]
\end{eqnarray*}
6.2 路面に作用する力に関する考察
運動方程式は,各質点の変位を用いて表現されているが,各接合部,接地部には,力が作用(発生)している.例えば,地面に作用している力(変動分)は,ばね定数$k_1$に発生している引張力の反力$f_1$である.方向は上向きと仮定されているが,実際に計算すると
\begin{eqnarray*}
f_1&=&k_1\left(x_1-u\right)=k_1\left[\frac{\left(\frac{p_a}{p}\right)^2-\left(\frac{\omega}{p}\right)^2}{{\left\{\left(\frac{\omega}{p}\right)^2-\left(\frac{p_1}{p}\right)^2\right\}\left\{\left(\frac{\omega}{p}\right)^2-\left(\frac{p_2}{p}\right)^2\right\}}}-1\right]a\sin\omega t \\
& = & k_1\left[\frac{\left(\frac{p_a}{p}\right)^2-\left(\frac{\omega}{p}\right)^2-\left(\frac{\omega}{p}\right)^4 + \left(\frac{\omega}{p} \right)^2\left\{\left(\frac{p_1}{p}\right)^2+\left(\frac{p_2}{p}\right)^2 \right\}-\left( \frac{p_1}{p}\right)^2\left(\frac{p_2}{p}\right)^2 }{{\left\{\left(\frac{\omega}{p}\right)^2-\left(\frac{p_1}{p}\right)^2\right\}\left\{\left(\frac{\omega}{p}\right)^2-\left(\frac{p_2}{p}\right)^2\right\}}}\right]a\sin\omega t
\end{eqnarray*}
ここで,
\begin{eqnarray*}
&& \left(\frac{p_1}{p}\right)^2+\left(\frac{p_2}{p}\right)^2=\left(\frac{k_1+k_2}{m_1}+\frac{k_2}{m_2}\right)\times\frac{m_1}{k_1}=1+\frac{m_2}{m_1}\left(\frac{p_a}{p}\right)^2+\left(\frac{p_a}{p}\right)^2 \\
&& \left(\frac{p_1}{p}\right)^2\left(\frac{p_2}{p}\right)^2=\frac{k_1}{m_1}\frac{k_2}{m_2}\times\left(\frac{m_1}{k_1}\right)^2=\left(\frac{p_a}{p}\right)^2
\end{eqnarray*}
となるので,質量比を$\beta=\frac{m_2}{m_1}$とおくと,次式のような形になる.
\begin{eqnarray*}
f_1= k_1\frac{\left(1+\beta\right)\left(\frac{p_a}{p}\right)^2-\left(\frac{\omega}{p}\right)^2 }{{\left\{\left(\frac{\omega}{p}\right)^2-\left(\frac{p_1}{p}\right)^2\right\}\left\{\left(\frac{\omega}{p}\right)^2-\left(\frac{p_2}{p}\right)^2\right\}}}\left(\frac{\omega}{p}\right)^2a\sin\omega t
\end{eqnarray*}
地面に作用する力は,この変動分と一定の自重分を加えた次式となる.
\begin{eqnarray*}
f_1' = - \left(m_1+m_2\right)g + f_1
\end{eqnarray*}
座標系を上向きを正としているので,重力の項が負で表現されるが下向きにかかる力,即ち,地面を押す力としては,
\begin{eqnarray*}
f_1'' = \left(m_1+m_2\right)g - f_1 = \left(m_1+m_2\right)g-k_1\frac{\left(1+\beta\right)\left(\frac{p_a}{p}\right)^2-\left(\frac{\omega}{p}\right)^2 }{{\left\{\left(\frac{\omega}{p}\right)^2-\left(\frac{p_1}{p}\right)^2\right\}\left\{\left(\frac{\omega}{p}\right)^2-\left(\frac{p_2}{p}\right)^2\right\}}}\left(\frac{\omega}{p}\right)^2a\sin\omega t
\end{eqnarray*}
6.3 粘性減衰を含む系の運動方程式に関する考察
図6-3(a)に示すような粘性減衰を含む系を考える.即ち,質量$m_1$と$m_2$の間にばねと並列に粘性減衰係数$c$のダシュポットを配し,減衰特性を含むモデルを考える.Free-body Diagramは,図(b)のようになり,並列に並べたばねとダシュポット共に引張力が発生すると考えるとそれぞれ次式となる.
\begin{eqnarray*}
&& f_k=k_2\left(x_2-x_1\right) \\
&& f_c=c\left(\dot{x}_2-\dot{x}_1\right)
\end{eqnarray*}
また,$f_1=k_1\left(x_1-u\right)$であるので,運動方程式は次のようになる.
\begin{eqnarray*}
&& m_1\ddot{x}_1 = -f_1 + f_k + f_c =-k_1\left(x_1-u\right) + k_2\left(x_2-x_1\right)+c\left(\dot{x}_2-\dot{x}_1\right) \\
&& m_2\ddot{x}_2 = -f_k - f_c = -k_1\left(x_2-x_1\right) - c\left(\dot{x}_2-\dot{x}_1\right)
\end{eqnarray*}
$k_1u$は,力の単位を持つので,$f_u=k_1u$とおき,整理すると次のような形となる.
\begin{eqnarray*}
&& m_1\ddot{x}_1 + c\dot{x}_1 - c\dot{x}_2 + \left(k_1+ k2\right)x_1 - k_1x_2 = f_u \\
&& m_2\ddot{x}_2 - c\dot{x}_1 + c\dot{x}_2 - k_2x_1 + k_2x_2 = 0
\end{eqnarray*}
この系は2自由度系であるが,多自由度系は次のような行列形式の運動方程式で記述されることが多い.
\begin{eqnarray*}
\mathbf{M}\ddot{\mathbf{x}} + \mathbf{C}\dot{\mathbf{x}} + \mathbf{K}{\mathbf{x}} = \mathbf{f}
\end{eqnarray*}
ここで,
\begin{eqnarray*}
\mathbf{x}=\left[\begin{array}{c} x_1 \\ x_2 \end{array}\right]
\text{, }
\dot{\mathbf{x}}=\left[\begin{array}{c} \dot{x}_1 \\ \dot{x}_2 \end{array}\right]
\text{, }
\ddot{\mathbf{x}}=\left[\begin{array}{c} \ddot{x}_1 \\ \ddot{x}_2 \end{array}\right]
\end{eqnarray*}
は,それぞれ,変位ベクトル,速度ベクトル,加速度ベクトルと呼ばれ,
\begin{eqnarray*}
\mathbf{f}=\left[\begin{array}{c} f_u \\ 0 \end{array}\right]
\end{eqnarray*}
は,力ベクトルと呼ばれる.また,
\begin{eqnarray*}
\mathbf{M}=\left[\begin{array}{cc}
m_1 & 0 \\ 0 & m_2
\end{array}\right]
\text{, }
\mathbf{C}=\left[\begin{array}{cc}
c & -c \\ -c & c
\end{array}\right]
\text{, }
\mathbf{K}=\left[\begin{array}{cc}
k_1+k_2 & -k_2 \\ -k_2 & k_2
\end{array}\right]
\end{eqnarray*}
は,それぞれ,質量行列,減衰行列,剛性行列と呼ばれる.
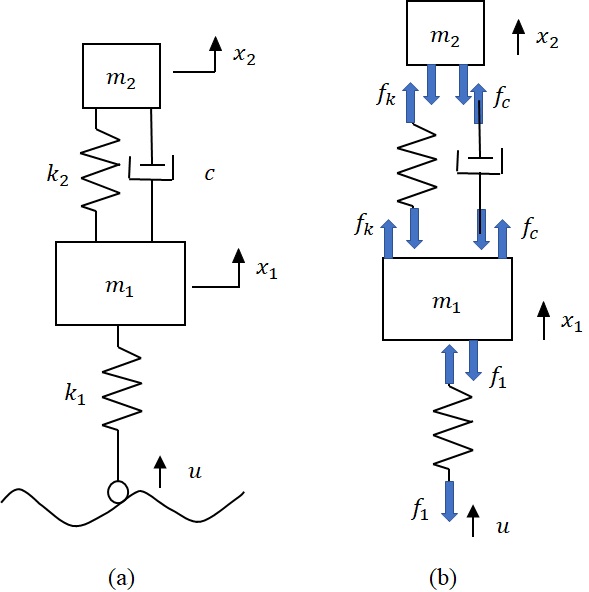
図6-3 粘性減衰を含む2自由度振動系モデル
6.4 Fourie変換による運動方程式の変換について
時間の関数である各質点の変位$x_j=x_j(t)$,および,力$f=f(t)$のFourie変換は角周波数$\omega$領域への変換は,虚数単位を$i$として,次式のように表すことができる.
\begin{eqnarray*}
X_j\left(\omega\right) = \int_{-\infty}^{\infty}x_j\left(t\right) e^{-i\omega t} \\
F\left(\omega\right) = \int_{-\infty}^{\infty}f\left(t\right) e^{-i\omega t}
\end{eqnarray*}
また,周波数$f$領域への変換の場合には,$\omega=2\pi f$となるだけなので,次式のようになる.
\begin{eqnarray*}
X_j\left(\omega\right) = \int_{-\infty}^{\infty}x_j\left(t\right) e^{-i2\pi ft} \\
F\left(\omega\right) = \int_{-\infty}^{\infty}f\left(t\right) e^{-i2\pi ft}
\end{eqnarray*}
ここで,$x_j\left(t\right)$は,$t=\pm\infty$で零になるとすると
\begin{eqnarray*}
&& \int_{-\infty}^{\infty}\dot{x}_j\left(t\right) e^{-i\omega t} =\left[x_j\left(t\right)e^{-i\omega t}\right] + i\omega\int_{-\infty}^{\infty}x_j\left(t\right) e^{-i\omega t}=i\omega X_j\left(\omega\right) \\
&& \int_{-\infty}^{\infty}\ddot{x}_j\left(t\right) e^{-i\omega t} = -\omega^2 X_j\left(\omega\right)
\end{eqnarray*}
となるので,質量行列,減衰行列,剛性行列が時間的に変化しない一定値となる場合には,行列形式で表した運動方程式をFourie変換することができ,次式のようになる.
\begin{eqnarray*}
&& \left(-\omega^2\mathbf{M} + i\omega\mathbf{C} + \mathbf{K}\right)\mathbf{X}\left(\omega\right) = \mathbf{F}\left(\omega\right) \\
&& \therefore \mathbf{X}\left(\omega\right) = \left(-\omega^2\mathbf{M} + i\omega\mathbf{C} + \mathbf{K}\right)^{-1}\mathbf{F}\left(\omega\right)
\end{eqnarray*}
力ベクトルのFourie変換ベクトルにかかっている係数行列は,”周波数応答関数行列”と呼ばれ,制御工学で学ぶ周波数伝達関数と同じものである.
6.5 演習
(1) 図6-4は,質量$m$の二つの物体A,Bがばね定数$k$のばねでつながれ,左端はばね定数$k$を介して壁に,右端は粘性減衰定数$c$のダシュポットを有する水平面上を滑らかに運動できる2自由度振動系を表している.ダシュポットの他端に$u(t)=a_0\sin\omega t$の周期的な変位入力を加える場合に対するA,Bの強制振動に対する運動方程式を導き,定常応答に対する振幅を式で示しなさい.
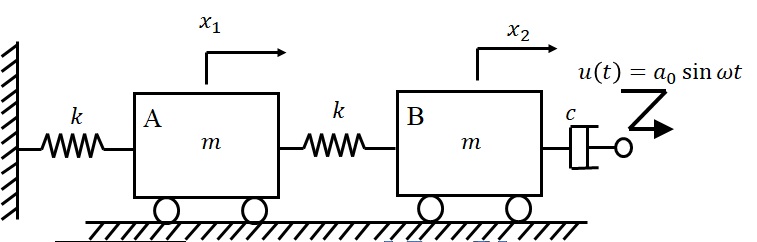
図6-4 ダシュポットを介した2自由度振動系の変位励振
(2) 図6-5は,質量$m_1$の台車がばね定数$k_1$のばねで壁に連結されており,台車上に設置された質量$m_2$の荷物がばね定数$k_2$のばねで台車と連結された系を表している.台車は地面に対して水平方向に滑らかに動くことができ,荷物もまた台車上を水平方向に滑らかに動くことができるとする.地盤が図に示すように水平方向に揺れている状態を考える.定常応答振幅を与えられた記号を用いて示し.定常応答振幅を与えられた記号を用いて示し,$m_1=10$[kg],$m_2=15$[kg],$k_1=1.75$[kN/m],$k_2=1.5$[kN/m]の系に対して,$a=1$ [cm]としたとき,$m_1$の応答振幅が最小となる角周波数$\omega$を求めよ.
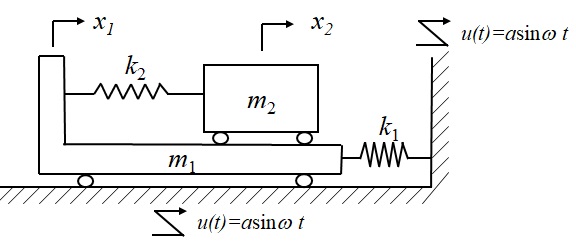
図6-5 変位励振を受ける2自由度振動系の定常応答





