7.動吸振器
7.1 粘性減衰系の周波数応答
機械力学Ⅰで学んだように,図7-1に示すような1自由度粘性減衰系に周期的な入力が作用する場合,その応答は自由振動応答と強制振動応答の和として表現される.一般に自由振動応答は時間と共に減衰していくことから,一般に,ある時間が経って定常的な応答になったと考えられる強制振動応答の特性が調べられる.特に,その周波数応答である,振動数応答曲線(振動振幅特性),位相差曲線である.

図7-1 1自由度粘性減衰系の強制振動
図7-2に1自由度粘性減衰系の周波数応答を示す.横軸は,無次元化周波数,即ち,系の固有角振動数$p=\sqrt{\frac{k}{m}}$に対する角周波数$\omega$の比をとっており,上側の図では,縦軸を無次元化振幅,即ち,静的な変位$\delta_e=P/k$に対する系の応答振幅$X$の比を示しており,下側は,入力に対する応答の位相遅れ$\phi$を取っている.粘性減衰係数$c$の値を大きくしていくと矢印に示す方向に各応答曲線は変化する.この図から分かるように,固有角振動数$p$が変化すると応答振幅が最大となる$\omega$の値が変化する.位相差に関しても,零から180度に変化する周波数$\omega$が変わると言える.また,粘性減衰係数$c$の値を変化させることによって,応答振幅の大きさを色々変化させることができる.このような特性を利用して,機械システムの振動応答を小さくする(制振する)方法として,動吸振器という考え方がある.
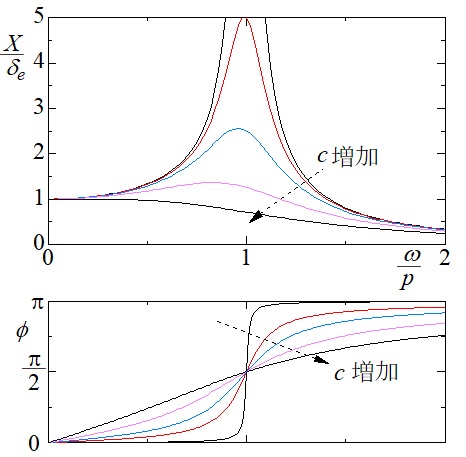
図7-2 1自由度振動系の周波数応答例
7.2 2自由度振動系による動吸振器の設計
機械システムに発生している振動低減に際しては,機械システムを図7-3(a)下図に示すように,質量$m_1$とばね定数$k_1$の1自由度系に周期的な強制外力$f(t)$が作用している系で主振動系としてモデル化し,それに副振動系を取り付けることにより振動低減を図る場合がある.副振動系は図に示すように,付加質量$m_2$がばね定数$k_2$と粘性減衰係数$c$で支持された系で,これを主振動系に連結し,図(b)に示すように2自由度振動系に変化させることで振動低減を図る.即ち,副振動系の付加質量$m_2$,ばね定数$k_2$,および,粘性減衰係数$c$の値を”うまく”調整することにより,$m_1$の振動を小さくするのが目的となる.即ち,これは,図7-3図(b)に示す系において,質量$m_1$の応答振幅(あるいは周波数特性)を制御する設計問題となる.

図7-3 動吸振器
7.3 2自由度振動系の振幅特性
図7-3(b)の系に対する運動方程式を導出し,振幅特性を求める.質量$m_1$,$m_2$の変位をそれぞれ,$x_1$,$x_2$とすると,Free-body Diagramは,図7-4のようになる.ばね,ダシュポットすべて引張力が発生していると仮定すると図に示す発生力は次のようになる.
\begin{eqnarray*}
\left.\begin{array}{l}
f_1 = k_1x_1 \\
f_k = k_2\left(x_2-x_1\right) \\
f_c = c\left(\dot{x}_2 - \dot{x}_1\right)
\end{array}\right\}
\end{eqnarray*}
と表現できるので,運動方程式は次のようになる.
\begin{eqnarray*}
&& m_1\ddot{x}_1 = f - f_1 + f_k + f_c = f - k_1x_1 + k_2\left(x_2 - x_1\right) + c\left(\dot{x}_2 - \dot{x}_1\right) \\
&& m_2\ddot{x}_2 = - f_k - f_c = -k_2\left(x_2-x_1\right) - c\left(\dot{x}_2 - \dot{x}_1\right)
\end{eqnarray*}
整理すると次式となる.
\begin{eqnarray*}
&& m_1\ddot{x}_1 + c\dot{x}_1 - c\dot{x}_2 + \left(k_1+k_2\right)x_1 - k_2x_2 = f \\
&& m_2\ddot{x}_2 - c\dot{x}_1 + c\dot{x}_2 - k_2x_1 + k_2x_2 = 0
\end{eqnarray*}
行列形式で表すと次のようになる.
\begin{eqnarray*}
\left[\begin{array}{cc}
m_1 & 0 \\
0 & m_2 \end{array}\right]
\left[\begin{array}{c}
\ddot{x}_1 \\ \ddot{x}_2
\end{array}\right] + \left[\begin{array}{cc}
c & -c \\
-c & c \end{array}\right]\left[\begin{array}{c}
\dot{x}_1 \\ \dot{x}_2 \end{array}\right]
+ \left[\begin{array}{cc}
k_1+k_2 & - k_2 \\
-k_2 & k_2 \end{array}\right]\left[\begin{array}{c}
x_1 \\ x_2 \end{array}\right] = \left[\begin{array}{c}
f \\ 0 \end{array}\right]
\end{eqnarray*}
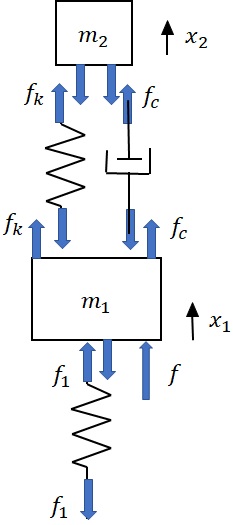
図7-4 動吸振器に対するFree-body Diagram
ここで,$x_j=x_j(t)$,および,力$f=f(t)$より,次のFourie変換を考える.
\begin{eqnarray*}
X_j\left(\omega\right) = \int_{-\infty}^{\infty}x_j\left(t\right) e^{-i\omega t} \\
F\left(\omega\right) = \int_{-\infty}^{\infty}f\left(t\right) e^{-i\omega t}
\end{eqnarray*}
即ち,運動方程式をFourie変換すると次式となる.
\begin{eqnarray*}
&& \left(-\omega^2\left[\begin{array}{cc}
m_1 & 0 \\
0 & m_2 \end{array}\right]
+ i\omega\left[\begin{array}{cc}
c & -c \\
-c & c \end{array}\right]
+ \left[\begin{array}{cc}
k_1+k_2 & - k_2 \\
-k_2 & k_2 \end{array}\right]\right)
\left[\begin{array}{c}
X_1\left(\omega\right) \\ X_2\left(\omega\right)
\end{array}\right] = \left[\begin{array}{c}
F\left(\omega\right) \\ 0 \end{array}\right] \\
&& \therefore \left[\begin{array}{cc}
k_1 + k_2 -m_1\omega^2 + i\omega c & -\left(k_2+i\omega c\right) \\
-\left(k_2+i\omega c\right) & k_2-m_2\omega^2 + i\omega c
\end{array}\right]
\left[\begin{array}{c}
X_1\left(\omega\right) \\ X_2\left(\omega\right)
\end{array}\right] = \left[\begin{array}{c}
F\left(\omega\right) \\ 0 \end{array}\right]
\end{eqnarray*}
よって,係数行列の逆行列を左からかけて変形する.
\begin{eqnarray*}
\left[\begin{array}{c}
X_1\left(\omega\right) \\ X_2\left(\omega\right)
\end{array}\right] &=&
\frac{1}{\left(k_1 + k_2 -m_1\omega^2 + i\omega c\right)\left(k_2-m_2\omega^2 + i\omega c\right)-\left(k_2+i\omega c\right)^2}
\left[\begin{array}{cc}
k_2-m_2\omega^2 + i\omega c & k_2+i\omega c \\
k_2+i\omega c & k_1 + k_2 -m_1\omega^2 + i\omega c
\end{array}\right]
\left[\begin{array}{c}
F\left(\omega\right) \\ 0 \end{array}\right] \\
&=& \frac{F\left(\omega\right)}{\left(k_1-m_1\omega^2\right)\left(k_2-m_2\omega^2\right)-k_2m_2\omega^2 + i\omega c\left\{k_1-\left(m_1+m_2\right)\omega^2\right\}}
\left[\begin{array}{c}
k_2-m_2\omega^2 + i\omega c \\ k_2+i\omega c \end{array}\right]
\end{eqnarray*}
分母,分子を$m_1$,$m_2$で割ると
\begin{eqnarray*}
\left[\begin{array}{c}
X_1\left(\omega\right) \\ X_2\left(\omega\right)
\end{array}\right]=
\frac{F\left(\omega\right)/m_1}{\left(\frac{k_1}{m_1}-\omega^2\right)\left(\frac{k_2}{m_2}-\omega^2\right)-\frac{k_2}{m_1}\omega^2 + i\omega\frac{ c}{m_2}\left\{\frac{k_1}{m_1}-\left(1+\frac{m_2}{m_1}\right)\omega^2\right\}}
\left[\begin{array}{c}
\frac{k_2}{m_2}-\omega^2 + i\omega\frac{c}{m_2} \\ \frac{k_2}{m_2}+i\omega\frac{c}{m_2} \end{array}\right]
\end{eqnarray*}
上式に現れる項は,主振動系,副振動系の固有振動特性に対応付ける事ができる.即ち,各不減衰固有角振動数を$p$,$p_a$とすると,
\begin{eqnarray*}
\frac{k_1}{m_1}=p^2\text{,}\quad \frac{k_2}{m_2}=p_a^2
\end{eqnarray*}
であり,入力振幅による静たわみ$\delta_{st}=F\left(\omega\right)/k_1$とすると,
\begin{eqnarray*}
F\left(\omega\right)/m_1=F\left(\omega\right)/k_1\frac{k_1}{m_1}=\delta_{st}p^2
\end{eqnarray*}
となる.また,主振動系に対する副振動系の質量比$\beta$の項
\begin{eqnarray*}
\beta = \frac{m_2}{m_1}
\end{eqnarray*}
も存在する.粘性減衰特性に関係する$\frac{c}{m_2}$の項に関しては,次の2通りの減衰比$\zeta$,$\zeta_a$を定めることができる.
\begin{eqnarray*}
&& \frac{c}{m_2}=2\left(\frac{c}{2m_2}\sqrt{\frac{m_1}{k_1}}\right)\sqrt{\frac{k_1}{m_1}} = 2\zeta p\\
&& \frac{c}{m_2}=2\left(\frac{c}{2\sqrt{m_2k_2}}\right)\sqrt{\frac{k_2}{m_2}} =2\zeta_ap_a
\end{eqnarray*}
即ち,両者の関係も含めて表すと,各減衰比の定義は次のようになる.
\begin{eqnarray*}
&& \zeta=\frac{c}{2m_2p}=\frac{c}{2m_2}\sqrt{\frac{m_1}{k_1}}=\frac{c}{2\sqrt{m_2k_2}}\sqrt{\frac{k_2}{m_2}}\sqrt{\frac{m_1}{k_1}}=\zeta_a\frac{p_a}{p}\\
&& \zeta_a=\frac{c}{2m_2p_a}=\frac{c}{2\sqrt{m_2k_2}}=\zeta\frac{p}{p_a}
\end{eqnarray*}
従って,応答振幅表現は,
\begin{eqnarray*}
\left[\begin{array}{c}
X_1\left(\omega\right) \\ X_2\left(\omega\right)
\end{array}\right]=
\frac{\delta_{st}p^2}{\left(p^2-\omega^2\right)\left(p_a^2-\omega^2\right)-\beta p_a^2\omega^2 + 2i\zeta p\omega\left\{p^2-\left(1+\beta\right)\omega^2\right\}}
\left[\begin{array}{c}
p_a^2-\omega^2 + 2i\zeta p\omega \\ p_a^2+2i\zeta p\omega \end{array}\right]
\end{eqnarray*}
$\zeta_a$を用いると,
\begin{eqnarray*}
\left[\begin{array}{c}
X_1\left(\omega\right) \\ X_2\left(\omega\right)
\end{array}\right]=
\frac{\delta_{st}p^2}{\left(p^2-\omega^2\right)\left(p_a^2-\omega^2\right)-\beta p_a^2\omega^2 + 2i\zeta_a p_a\omega\left\{p^2-\left(1+\beta\right)\omega^2\right\}}
\left[\begin{array}{c}
p_a^2-\omega^2 + 2i\zeta_a p_a\omega \\ p_a^2+2i\zeta_a p_a\omega \end{array}\right]
\end{eqnarray*}
分母,分子を$p^4$で割る.$\zeta$で表現すると,
\begin{eqnarray*}
\left[\begin{array}{c}
X_1\left(\omega\right) \\ X_2\left(\omega\right)
\end{array}\right]=
\frac{\delta_{st}}{\left\{1-\left(\frac{\omega}{p}\right)^2\right\}\left\{\left(\frac{p_a}{p}\right)^2-\left(\frac{\omega}{p}\right)^2\right\}-\beta\left(\frac{p_a}{p}\right)^2\left(\frac{\omega}{p}\right)^2 + 2i\zeta \left(\frac{\omega}{p}\right)\left\{1-\left(1+\beta\right)\left(\frac{\omega}{p}\right)^2\right\}}
\left[\begin{array}{c}
\left(\frac{p_a}{p}\right)^2-\left(\frac{\omega}{p}\right)^2 + 2i\zeta \frac{\omega}{p} \\ \left(\frac{p_a}{p}\right)^2+2i\zeta \frac{\omega}{p} \end{array}\right]
\end{eqnarray*}
$\zeta_a$で表現した場合は,
\begin{eqnarray*}
\left[\begin{array}{c}
X_1\left(\omega\right) \\ X_2\left(\omega\right)
\end{array}\right]=
\frac{\delta_{st}}{\left\{1-\left(\frac{\omega}{p}\right)^2\right\}\left\{\left(\frac{p_a}{p}\right)^2-\left(\frac{\omega}{p}\right)^2\right\}-\beta\left(\frac{p_a}{p}\right)^2\left(\frac{\omega}{p}\right)^2 + 2i\zeta_a \left(\frac{p_a}{p}\right)\left(\frac{\omega}{p}\right)\left\{1-\left(1+\beta\right)\left(\frac{\omega}{p}\right)^2\right\}}
\left[\begin{array}{c}
\left(\frac{p_a}{p}\right)^2-\left(\frac{\omega}{p}\right)^2 + 2i\zeta_a \frac{p_a}{p}\frac{\omega}{p} \\ \left(\frac{p_a}{p}\right)^2+2i\zeta_a \frac{p_a}{p}\frac{\omega}{p} \end{array}\right]
\end{eqnarray*}
更に,$\Omega =\omega/p$,$\mu=p_a/p$とおくと,主振動系の応答振幅の$\zeta$を用いた場合は
\begin{eqnarray*}
X_1\left(\Omega\right)=
\frac{\mu^2-\Omega^2 + 2i\zeta \Omega}{\left(1-\Omega^2\right)\left(\mu^2-\Omega^2\right)-\beta\mu^2\Omega^2 + 2i\zeta \Omega\left\{1-\left(1+\beta\right)\Omega^2\right\}}\delta_{st}
\end{eqnarray*}
一方,$\zeta_a$を用いた表現では次のようになる.
\begin{eqnarray*}
X_1\left(\Omega\right)=
\frac{\mu^2-\Omega^2 + 2i\zeta_a \mu\Omega}{\left(1-\Omega^2\right)\left(\mu^2-\Omega^2\right)-\beta\mu^2\Omega^2 + 2i\zeta_a \mu\Omega\left\{1-\left(1+\beta\right)\Omega^2\right\}}\delta_{st}
\end{eqnarray*}
各記号の意味は次の通りとなる.
$\Omega=\frac{\omega}{p}$:無次元化(角)周波数$\ldots$独立変数($\omega$に対応)
$\mu=\frac{p_a}{p}$:主振動系と副振動系の(不減衰)固有角振動数比
$\beta=\frac{m_2}{m_1}$:主振動系と副振動系の質量比
$\zeta=\frac{c}{2m_2p}$:主振動系の固有角振動数を用いた減衰比
$\zeta_a=\frac{c}{2\sqrt{m_2k_2}}$:副振動系の減衰比
ここで,応答振幅は,複素振幅であり,分母,分子とも複素数で次の形式である.
\begin{eqnarray*}
X_1\left(\Omega\right) = X_1 = \frac{c+di}{a+bi} = \frac{\left(c+di\right)\left(a-bi\right)}{a^2+b^2} = \frac{1}{a^2+b^2}\left\{\left(ac+bd\right)+\left(ad-bc\right)i \right\}
\end{eqnarray*}
よって大きさは次のようになる.
\begin{eqnarray*}
\left|X_1\right|^2 = \frac{1}{\left(a^2+b^2\right)^2}\left\{\left(ac+bd\right)^2+\left(ad-bc\right)^2 \right\} = \frac{1}{\left(a^2+b^2\right)^2}\left\{\left(ac\right)^2+\left(bd\right)^2+\left(ad\right)^2+\left(bc\right)^2 \right\} = \frac{c^2+d^2}{a^2+b^2}
\end{eqnarray*}
従って,応答振幅を$\delta_{st}$で割って定まる主振動系の無次元化応答曲線の大きさは次のようになる.
\begin{eqnarray*}
\left(\frac{X_1}{\delta_{st}}\right)^2 =
\frac{\left(\mu^2-\Omega^2\right)^2 + 4\zeta^2 \Omega^2}{\left\{\left(1-\Omega^2\right)\left(\mu^2-\Omega^2\right)-\beta\mu^2\Omega^2\right\}^2 + 4\zeta^2 \Omega^2\left\{1-\left(1+\beta\right)\Omega^2\right\}^2}
\end{eqnarray*}
あるいは,
\begin{eqnarray*}
\left(\frac{X_1}{\delta_{st}}\right)^2 =
\frac{\left(\mu^2-\Omega^2\right)^2 + 4\zeta_a^2 \mu^2\Omega^2}{\left\{\left(1-\Omega^2\right)\left(\mu^2-\Omega^2\right)-\beta\mu^2\Omega^2\right\}^2 + 4\zeta_a^2 \mu^2\Omega^2\left\{1-\left(1+\beta\right)\Omega^2\right\}^2}
\end{eqnarray*}
上記が動吸振器に応用される基礎式である.両式の違いは,$\zeta$と$\mu\zeta_a$という表現の違いのみなので,今後は前者の式を用いて関係式を導くことにする.
7.4 定点理論によるパラメータ設定
無次元された加振周波数$\Omega$に対して,$\delta_{st}$に対する主振動系の応答振幅$|X_1|$をプロットすると図7-5のような結果が得られる.各パラメータは,図に示すように,主振動系と副振動系の質量比を$\beta=\frac{m_2}{m_1}=0.05$とし,固有角振動数比を$\mu=\frac{p_a}{p}=1$とした場合について,減衰比を$\zeta=0.001$,$0.1$,$0.3$と徐々に大きくした結果を示している.この図は”応答曲線”,”変位共振曲線”などと呼ばれ,様々なパラメータに対して,減衰が小さい場合は,2個の共振点が現れ,減衰を大きくしていくと共振点の山がつぶれ,共振点が1つになるといった変化を示す.更に,その際,$\zeta$の値に対して特徴的な変化をしていることが分かる.即ち,次の理論が成り立つ.
定点理論:応答曲線$|X_1|$には,$m_1$,$m_2$,$k_1$,$k_2$が定まった場合,$\zeta$,即ち,粘性減衰係数$c$をどんな値に変化させても必ず通る点が2点存在する.
図7-5の例では,図中に示した点P,Qが定点であり,パラメータを変えるとこの位置は当然変化する.本理論の証明は,煩雑となるので省略するが,様々なパラメータに対して実際に計算し確かめてみると良い(かもしれない).動吸振器の設計に際しては,この性質を利用して,副振動系の設計値を定めていくことになる.

図7-5 動吸振器に対するFree-body Diagram
定点位置に対応する無次元周波数
定点P,Qの2点に対応する周波数における関係式を考える.2点を定めるために,$\zeta\rightarrow\infty$と$\zeta=0$の場合を考える.
$\zeta\rightarrow\infty$とすると,
\begin{eqnarray*}
\left|\frac{X_1}{\delta_{st}}\right| = \sqrt{\frac{4\zeta^2\Omega^2}{4\zeta^2\Omega^2\left\{1-\left(1+\beta\right)\Omega^2\right\}^2}} = \frac{1}{\left|1-\left(1+\beta\right)\Omega^2\right|}
\end{eqnarray*}
$\zeta=0$とすると,
\begin{eqnarray*}
\left|\frac{X_1}{\delta_{st}}\right| = \left|\frac{\mu^2-\Omega^2}{\left(1-\Omega^2\right)\left(\mu^2-\Omega^2\right)-\beta\mu^2\Omega^2}\right|
\end{eqnarray*}
定点P,Qでは,この2点が同じ値を取ることになるが,この2つの条件においては,大きさは同じとなるが,符号は逆となる.よって,次式が成立する.
\begin{eqnarray*}
\frac{1}{1-\left(1+\beta\right)\Omega^2} = - \frac{\mu^2-\Omega^2}{\left(1-\Omega^2\right)\left(\mu^2-\Omega^2\right)-\beta\mu^2\Omega^2}
\end{eqnarray*}
変形すると
\begin{eqnarray*}
\left(1-\Omega^2\right)\left(\mu^2-\Omega^2\right)-\beta\mu^2\Omega^2=- \left\{1-\left(1+\beta\right)\Omega^2\right\}\left(\mu^2-\Omega^2\right)
\end{eqnarray*}
左辺に移項すると,
\begin{eqnarray*}
\left(1-\Omega^2\right)\left(\mu^2-\Omega^2\right)-\beta\mu^2\Omega^2+ \left\{1-\left(1+\beta\right)\Omega^2\right\}\left(\mu^2-\Omega^2\right) = 0 \\
\end{eqnarray*}
$\Omega^n$でまとめることを考えて,括弧を開く.
\begin{eqnarray*}
&& \Omega^4 -\left(1+\mu^2\right)\Omega^2 + \mu^2 - \beta\mu^2\Omega^2 + \mu^2 - \left\{1+\mu^2\left(1+\beta\right)\right\}\Omega^2 + \left(1+\beta\right)\Omega^4 = 0
\end{eqnarray*}
まとめると
\begin{eqnarray*}
\left(2+\beta\right)\Omega^4 - 2\left\{1+\mu^2\left(1+\beta\right)\right\}\Omega^2 + 2\mu^2 = 0
\end{eqnarray*}
よって,次の$\Omega$に関する4次方程式を得る.
\begin{eqnarray*}
\Omega^4 - 2\frac{1+\mu^2\left(1+\beta\right)}{2+\beta}\Omega^2 + \frac{2\mu^2}{2+\beta} = 0
\end{eqnarray*}
また,途中で出てきた
\begin{eqnarray*}
\left(1-\Omega^2\right)\left(\mu^2-\Omega^2\right)-\beta\mu^2\Omega^2=- \left\{1-\left(1+\beta\right)\Omega^2\right\}\left(\mu^2-\Omega^2\right)
\end{eqnarray*}
の関係も定点P,Qでは成立している(後でこの関係を変形に利用する).ここで,定点P,Qに対応する無次元周波数をそれぞれ$\Omega_1$,$\Omega_2$とすると,解と係数の関係から次式が成り立つ.
\begin{eqnarray*}
&& \Omega_1^2+ \Omega_2^2 = \frac{2\left\{1+\mu^2\left(1+\beta\right)\right\}}{2+\beta} \\
&& \Omega_1^2\Omega_2^2 = \frac{2\mu^2}{2+\beta}
\end{eqnarray*}
最適調整
動吸振器ではどの周波数においても応答振幅をできるだけ下げたい,という要請があるのでまずは定点P,Qの高さを同じし,かつ,その高さをできるだけ低く,即ち,応答振幅を小さくするようなパラメータの組み合わせ考える.
$\zeta\rightarrow\infty$に対して,点P,Qの高さが同じとなるのは,
\begin{eqnarray*}
&& \frac{1}{1-\left(1+\beta\right)\Omega_1^2} = -\frac{1}{1-\left(1+\beta\right)\Omega_2^2} \\
&& \left(1+\beta\right)\left(\Omega_1^2+\Omega_2^2\right) = 2 \\
&& \therefore \Omega_1^2+\Omega_2^2 = \frac{2}{1+\beta}
\end{eqnarray*}
よって,解と係数の関係から出てきた前の関係を使うと次式となる.
\begin{eqnarray*}
&& \frac{1+\mu^2\left(1+\beta\right)}{2+\beta} = \frac{2}{1+\beta} \\
&& \therefore \mu = \frac{1}{1+\beta}
\end{eqnarray*}
即ち,この関係が成立する$\mu$を最適値$\mu_{opt}$として定める.
\begin{eqnarray*}
\mu_{opt} = \frac{1}{1+\beta} \Rightarrow \frac{p_a}{p}=\frac{1}{1+\frac{m_2}{m_1}}
\end{eqnarray*}
よって
\begin{eqnarray*}
&& \frac{k_2}{m_2}\frac{m_1}{k_1}=\frac{1}{\left(1+\frac{m_2}{m_1}\right)^2} \\
&& \therefore k_2 = k_1\frac{\frac{m_2}{m_1}}{\left(1+\frac{m_2}{m_1}\right)^2}=k_1\frac{\beta}{\left(1+\beta\right)^2}
\end{eqnarray*}
この結果から,動吸振器の設計では,まず,”副振動系の付加質量$m_2$”を定め,その値に基づき定まる副振動系のばね定数$k_2$の値を上式で求めることになる.この一連の作業を”最適調整”という場合がある.
最適減衰
最適調整より定められた$\mu=\frac{1}{1+\beta}$を用いると定点P,Qにおいて
\begin{eqnarray*}
&& \Omega^4 - 2\frac{1+\frac{1}{1+\beta}}{2+\beta}\Omega^2 + \frac{2}{\left(2+\beta\right)\left(1+\beta\right)^2} = 0 \\
&& \therefore \Omega^4 - \frac{2}{1+\beta}\Omega^2 + \frac{2}{\left(2+\beta\right)\left(1+\beta\right)^2} = 0
\end{eqnarray*}
この式を2次方程式と見なして解くと
\begin{eqnarray*}
\Omega^2 = \frac{1}{1+\beta}\mp\sqrt{\frac{1}{\left(1+\beta\right)^2} - \frac{2}{\left(2+\beta\right)\left(1+\beta\right)^2} }
\end{eqnarray*}
よって,点P,Qに関して
\begin{eqnarray*}
\left.\begin{array}{l}
\Omega_1^2 \\ \Omega_2^2
\end{array}\right\} = \frac{1}{1+\beta}\left(1\mp\sqrt{\frac{\beta}{2+\beta} }\right)
\end{eqnarray*}
この2点で$\left(X_1/\delta_{st}\right)^2$が極大(最大)となる$\zeta$を定めるために,次の関係を用いる.即ち,$\Omega_1$,$\Omega_2$において,
\begin{eqnarray*}
\frac{\partial}{\partial\Omega^2}\left\{\left(X_1/\delta_{st}\right)^2\right\}=0
\end{eqnarray*}
となる,減衰比$\zeta$を求め,最適調整の関係$\mu=\frac{1}{1+\beta}$も同時に成り立つ関係式を求める.関係式
\begin{eqnarray*}
\left(\frac{X_1}{\delta_{st}}\right)^2 =
\frac{\left(\mu^2-\Omega^2\right)^2 + 4\zeta^2 \Omega^2}{\left\{\left(1-\Omega^2\right)\left(\mu^2-\Omega^2\right)-\beta\mu^2\Omega^2\right\}^2 + 4\zeta^2 \Omega^2\left\{1-\left(1+\beta\right)\Omega^2\right\}^2}
\end{eqnarray*}
において,$x=\Omega^2$と置き直す.即ち,
\begin{eqnarray*}
\frac{\left(\mu^2-x\right)^2 + 4\zeta^2 x}{\left\{\left(1-x\right)\left(\mu^2-x\right)-\beta\mu^2x\right\}^2 + 4\zeta^2 x\left\{1-\left(1+\beta\right)x\right\}^2} \equiv f\left(x\right)
\end{eqnarray*}
において,$\frac{df}{dx}=0$の関係を求める.
\begin{eqnarray*}
\frac{df}{dx}&=&\left[\left\{\left(1-x\right)\left(\mu^2-x\right)-\beta\mu^2x\right\}^2 + 4\zeta^2 x\left\{1-\left(1+\beta\right)x\right\}^2\right]^{-2}\left(
\left\{-2\left(\mu^2-x\right)+4\zeta^2\right\}\left[\left\{\left(1-x\right)\left(\mu^2-x\right)-\beta\mu^2x\right\}^2 + 4\zeta^2 x\left\{1-\left(1+\beta\right)x\right\}^2\right]\right. \\
&-& \left\{\left(\mu^2-x\right)^2 + 4\zeta^2 \right\} \left[2\left\{-\left(\mu^2-x\right)-\left(1-x\right)-\beta\mu^2\right\}\left\{\left(1-x\right)\left(\mu^2-x\right)-\beta\mu^2x\right\} \right.\\
&+& \left. 4\zeta^2\left\{1-\left(1+\beta\right)x\right\}^2-8\left(1+\beta\right)\zeta^2 x\left\{1-\left(1+\beta\right)x\right\}\right)
\end{eqnarray*}
ここで,定点P,Qで成立している以下の関係式を代入する.
\begin{eqnarray*}
&& \left(1-\Omega^2\right)\left(\mu^2-\Omega^2\right)-\beta\mu^2\Omega^2=- \left\{1-\left(1+\beta\right)\Omega^2\right\}\left(\mu^2-\Omega^2\right)\\
&&\therefore \left(1-x\right)\left(\mu^2-x\right)-\beta\mu^2x=- \left\{1-\left(1+\beta\right)x\right\}\left(\mu^2-x\right)
\end{eqnarray*}
即ち,代入して整理すると次のようになる.
\begin{eqnarray*}
\frac{df}{dx} =\frac{\left\{1-\left(1+\beta\right)x\right\}\left\{\left(\mu^2-x\right)^2 + 4\zeta^2 \right\}}{\left[\left\{\left(1-x\right)\left(\mu^2-x\right)-\beta\mu^2x\right\}^2 + 4\zeta^2 x\left\{1-\left(1+\beta\right)x\right\}^2\right]^2} \left[4\left(1+\beta\right)x\zeta^2
-\left(\mu^2-x\right)\left\{2+\left(1+\beta\right)\mu^2-\left(3+\beta\right)\right\}
\right]
\end{eqnarray*}
従って,
\begin{eqnarray*}
4\left(1+\beta\right)x\zeta^2-\left(\mu^2-x\right)\left\{2+\left(1+\beta\right)\mu^2-\left(3+\beta\right)\right\} = 0
\end{eqnarray*}
となる$\zeta$を定めれば,定点$\Omega_1$,$\Omega_2$において,$\frac{df}{dx}=0$とすることができる.即ち,$\zeta$が
\begin{eqnarray*}
\zeta^2=\frac{\left(\mu^2-x\right)\left\{2+\mu^2+\beta\mu^2-\left(3+\beta\right)x\right\}}{4\left(1+\beta\right)x}
=\frac{\left(\mu^2-\Omega^2\right)\left\{2+\mu^2+\beta\mu^2-\left(3+\beta\right)\Omega^2\right\}}{4\left(1+\beta\right)\Omega^2}
\end{eqnarray*}
のとき,$f\left(x\right)=f\left(\Omega^2\right)$は$\Omega_1$,$\Omega_2$において極値を取ることになる.$x=\Omega^2=\frac{1}{1+\beta}$においても$\frac{df}{dx}=0$であり,
\begin{eqnarray*}
\Omega_1^2= \frac{1}{1+\beta}\left(1-\sqrt{\frac{\beta}{2+\beta}}\right) < \frac{1}{1+\beta} < \Omega_2^2= \frac{1}{1+\beta}\left(1+\sqrt{\frac{\beta}{2+\beta}}\right)
\end{eqnarray*}
となるので,関数$f\left(x\right)=f\left(\Omega^2\right)$の増減表を作成すると次のようになる.
$f\left(x\right)=\left(\frac{X_1\left(\Omega\right)}{\delta_st}\right)^2の$増減表
| 無次元周波数$\Omega$ | 0.0 | | $\Omega_1$ | | $\sqrt{\frac{1}{1+\beta}}$ | | $\Omega_2$ | |
| $\frac{df}{dx}$ | | $+$ | $0$ | $-$ | $0$ | $+$ | $0$ | $-$ |
| $f$ | | $\nearrow$ | 極大 | $\searrow$ | 極小 | $\nearrow$ | 極大 | $\searrow$ |
即ち,$\Omega^2=0$から$f$は増大し$\Omega_1^2$で極大となり,$\Omega^2=\frac{1}{1+\beta}$で一旦極小となった後,$\Omega_2^2$で再び極大を取り,次第に小さくなることがわかる.
最適減衰は,最適調整の関係
\begin{eqnarray*}
\mu= \mu_{opt} = \frac{1}{1+\beta}
\end{eqnarray*}
を考慮して,$\Omega_1^2$,$\Omega_2^2$を代入すると次の2つの式が定まる.
\begin{eqnarray*}
\begin{array}{ll}
\Omega^2=\Omega_1^2 \text{:} & \zeta_1^2 =\frac{\beta}{8\left(1+\beta\right)^3}\left(3-\sqrt{\frac{\beta}{\beta+2}}\right) \\
\Omega^2=\Omega_2^2 \text{:} & \zeta_2^2 =\frac{\beta}{8\left(1+\beta\right)^3}\left(3+\sqrt{\frac{\beta}{\beta+2}}\right) \\
\end{array}
\end{eqnarray*}
これより,次のように2次形式で平均化して減衰比を定める.
\begin{eqnarray*}
&& \zeta_{opt}^2 =\frac{\zeta_1^2+\zeta_2^2}{2} =\frac{3\beta}{8\left(1+\beta\right)^3} \\
&& \therefore \zeta_{opt} =\sqrt{\frac{3\beta}{8\left(1+\beta\right)^3}}
\end{eqnarray*}
すでに副振動系の質量$m_2$,ばね定数$k_2$の値は定まっているので,この関係式より,粘性減衰係数$c$の値を定めることができることになる.ここで示した減衰比の定め方を最適減衰と呼ぶ場合がある.
減衰比の定義を$\zeta_a$とすると,$\zeta_a=\zeta/\mu$となるので,最適減衰の計算式は次式となる.
\begin{eqnarray*}
\zeta'_{opt} = \zeta/\mu = \zeta\left(1+\beta\right) = \sqrt{\frac{3\beta}{8\left(1+\beta\right)}}
\end{eqnarray*}
定式化を間違えている教科書が散見されるので,定義を確認することを薦める.
7.5 演習
(1) 実際に質量が$m_1=100$kg,ばね定数$k_1=5\times10^5$N/mである主振動系に,質量$m_2$,ばね定数$k_2$,粘性減衰定数$c$の副振動系を設置し,振動低減を図る.$m_2=10$kgとした場合の最適調整,最適減衰となる$k_2$,$c$を定め,主振動系の応答をエクセル等を用いて計算し,グラフ化せよ.





