�W�D���O�����W���������T
8.1 �^���������̓��o
�@���̂Â���ɍۂ��ẮC�������ۂ��������C��������C���p����C���䂷��C���Ƃ������I�ȕ��@�����łȂ��C���_�I�ȕ��@�C�����C���_��͂ɂ����g�ޕK�v������D���̂��߂ɂ́C�������ۂ́h�����i�C���[�W���j�h�C���ۉ��i�����\���j�h�̗������K�v�s���ƂȂ�D�@�B�͊w�Ŏ�舵���^���̃C���[�W���Ƃ��āC�́F�͂Ɖ^���QNewton�̑�Q�@������{�Ƃ��āC�^���������̓��o�i�������j���s���Ă������C���G�Ȍ��ۂ̗����ɓ������ẮC���ʓI�Ȋϓ_����̃A�v���[�`���菕���ƂȂ肦�C�^���ʂƗ͐ρF�͂ƍ�p���Ԃ�G�l���M�[�F�͂ƈړ��ʂƂ������T�O����̃C���[�W������̓��o���K�v�ȏꍇ������D���ɁC�h�G�l���M�[�h�Ƃ����T�O�́C�^���ɂ�����^���G�l���M�[�����łȂ��C�d�C�E�d�q�G�l���M�[�C���w�G�l���M�[�ȂǑ��̕���ɂ����Ă��C���[�W���ɗ��p�ł�����̂ł���̂ŁC���̂̉^�����d�C�I�ω��≻�w�I�ω����悤�Ȍ��ۂ��l����ۂɂ́C�����̑��ݍ�p����т����l�����ōs���K�v�ƂȂ�D�ŏI�I�ɂ́C���ݍ�p�����f���ꂽ�h��b�������h�o���C����Ɋ�Â���͂����{���C���ۂɂ��Ē��ׂ�Ƃ������ƂɂȂ�D�����ł́C�^���������̓��o�ɍۂ��āC���ɂȂ�l�����̃C���[�W�ɂ��Ă������l�@���Ă݂�D
�@���W�n��ݒ肵�C�ψʁi�x�N�g���j$\mathbf{x}$�Ƃ��̎��Ԕ����̑��x�x�N�g��$\dot{\mathbf{x}}$�C$\ldots$�C�y�э�p�̓x�N�g��$\mathbf{f}$���`����D
�@ Newton's second law of motion
�@���x�x�N�g���C�̓x�N�g���̗v�f�����ɗl�Ɉ�ʓI�ɕ\�킷���Ƃɂ���D
\begin{eqnarray*}
&& \mathbf{v}=\left[\begin{array}{cccc}
v_1\text{,} & v_2\text{,}&\ldots\text{,}&v_n
\end{array}\right]^T \\
&& \mathbf{f}=\left[\begin{array}{cccc}
f_1\text{,} & f_2\text{,}&\ldots\text{,}&f_n
\end{array}\right]^T
\end{eqnarray*}
����$m$�̒P��̎��_�ɑ��ĉ^���@���C�����C�j���[�g���̂��Q�@�������Ŏ�����
\begin{eqnarray*}
\frac{d}{dt}\left(m\mathbf{v}\right)=\mathbf{f}
\end{eqnarray*}
�ΏۂƂ���n�ɑ��āC���ʍs��$\mathbf{M}$���ł���ꍇ�́C�����̂悤�ɋL�q�ł���D
\begin{eqnarray*}
\frac{d}{dt}\left(\mathbf{M}\mathbf{v}\right)=\mathbf{f}
\end{eqnarray*}
�A d'Alembert's principle(�_�����x�[���̌���)
�u�j���[�g���̑�Q�@���ōl���鍶�ӂ������͂Ƃ����͂Ƃ��ĉ��߂��āC�ÓI�Ȓލ����Ɠ�����������l�����v
�����C�����͂�$\mathbf{f}_I$�Ƃ��āC�S�̂Ƃ��ė͂��ނ荇���Ă���ƍl�����
\begin{eqnarray*}
\mathbf{f} + \mathbf{f}_I = \mathbf{0}
\end{eqnarray*}
�����ŁC�E�ӂ͗�x�N�g���ł���C�P�ꎿ�_�ɑ���
\begin{eqnarray*}
\mathbf{f}_I = -\frac{d}{dt}\left(m\mathbf{v}\right)
\end{eqnarray*}
�Ȃ�h�����́h���`����Ǝ��̊W����D
\begin{eqnarray*}
\mathbf{f} -\frac{d}{dt}\left(m\mathbf{v}\right) = \mathbf{0}
\end{eqnarray*}
�j���[�g���̑�Q�@���̕ό`�ɉ߂��Ȃ����C���ׂė͂ōl����Ƃ����l�����ōޗ��͊w��e���͊w�̕���ł͂��̍l�������悭�p������D
�B �G�l���M�[�ۑ���
�G�l���M�[�ۑ��������ꂪ���藧�悤�ȉ^����Ԃł���C���̍l�����ʼn^�������������߂邱�Ƃ��ł���i�ƍl������j�D�����C�n�̉^���G�l���M�[��$T$�C�|�e���V�����G�l���M�[��$U$�Ƃ���Ƃ��C�͊w�I�G�l���M�[�ۑ����́C$T+U=$��� �ƂȂ�̂ŁC��������ԂŔ�������Ǝ����ƂȂ�D
\begin{eqnarray*}
\frac{d}{dt}\left(T+U\right) = 0
\end{eqnarray*}
�Ⴆ�C�}8-1�Ɏ����P���R�x��-���_�n�Ɋւ��Ă��̊W���l���Ă݂�D����$m$�̕��̂�$x$�ψʂ��C�˒萔$k$�̂˂�$x$�L�сC���̎��̑��x��$\dot{x}$�Ƃ���Ɖ^���G�l���M�[�C�|�e���V�����G�l���M�[�͂��ꂼ�ꎟ�̂悤�ɂȂ�D
\begin{eqnarray*}
&& T = \frac{1}{2}m\dot{x}^2 \\
&& U = \frac{1}{2}kx^2
\end{eqnarray*}
�����
\begin{eqnarray*}
\frac{d}{dt}\left(T+U\right) = \frac{d}{dt}\left(\frac{1}{2}m\dot{x}^2+\frac{1}{2}kx^2\right) = 0
\end{eqnarray*}
�����C
\begin{eqnarray*}
&& m\ddot{x}\dot{x} + kx\dot{x} =0 \\
&& \therefore \dot{x}\left(m\ddot{x} + kx\right) = 0
\end{eqnarray*}
���̎����C�h�C�ӂ�$\dot{x}$�ɑ��Đ��藧���߂ɂ́h�ƍl����ƁC
\begin{eqnarray*}
m\ddot{x} + kx = 0
\end{eqnarray*}
�Ƃ����悭�m��ꂽ�P���R�x�n�̉^���������ƂȂ�D

�}8-1�@�P���R�x��-���_�n�̐U��
�@
�C Principle of virtual work(���z�d���̌���)
�@����͊w����l���C�u�ނ荇����Ԃɂ���n�ɉ��z�d��$\delta\mathbf{x}$��^�����ꍇ�C�����łɓ����Ă���͎͂d�������Ȃ��v�Ƃ����l�����ł���C�x�N�g���ʂŕ\�������͂̒ލ������d���C�܂�C�G�l���M�[�ɑΉ�����X�J���[�ʂɕϊ����čl����l�����ŁC��p��$\mathbf{f}$�ɂ��d��$W_f$�Ɗ�����$\mathbf{f}_I$�����z�ψʂɑ��Ă���d��
\begin{eqnarray*}
&& W_f = \mathbf{f}\cdot\delta\mathbf{x} \\
&& W_I = \mathbf{f}_I\cdot\delta\mathbf{x} = - \frac{d}{dt}\left(m\mathbf{f}\right)\cdot\delta\mathbf{x}
\end{eqnarray*}
�Ɋւ��āC���z�d���̌�����K�p����ƁC
\begin{eqnarray*}
&& W_f + W_I = 0 \\
&& \therefore \mathbf{f}\cdot\delta\mathbf{x} + \left\{-\frac{d}{dt}\left(m\mathbf{f}\right)\cdot\delta\mathbf{x}\right\} =0
\end{eqnarray*}
�Ƃ������莮���ɂȂ�D
�@�M�͊w���@���Ƃ̊֘A���l����Ɨl�X�Ȍ��ۂ��G�l���M�[�Ǝd���Ƃ����`�ő����C�S�̂̊W�����C�����C��b�������o����Ƃ��������́C����ʓI�ȕ��@�Ƃ��ė��p�ł���ł͂Ȃ����Ƃ������Ƃ��\�z�����i��������Ȃ��j�D�����ŁC�n�̎��G�l���M�[��Ȃ����d�����l���邱�Ƃɂ��C�^���������o������@�ɂ��čl�@����D
8.2 ��ʍ��W�Ɖ��z�ψ�
�@���̂̏�Ԃ�����ʓI�ɕ\�����邽�߂ɁC��ʍ��W�Ƃ����T�O���������D�����C���R�x��$N$�ł���n���l���C���̌n�̎��R�x�Ɠ�������$N$�݂̌��ɓƗ��ȕϐ��ŕ\���\�ƂȂ鎟�̂悤�Ȉ�ʍ��W���l����D
\begin{eqnarray*}
q_k = q_k\left(t\right) \quad\left(k=1,2,\ldots,N\right)
\end{eqnarray*}
�ΏۂƂ���n��$n$�̓_�̂R�����ʒu���W�����W�n�ŕ\�킷���Ƃɂ��C��ʍ��W�ƑΉ��t���Ĉȉ��̂悤�ɕ\�����邱�Ƃɂ���D
\begin{eqnarray*}
\left.\begin{array}{l}
x_i = x_i\left(q_1,\ q_2,\ \ldots ,\ q_N,\ t\right) \\
y_i = y_i\left(q_1,\ q_2,\ \ldots ,\ q_N,\ t\right) \\
z_i = x_i\left(q_1,\ q_2,\ \ldots ,\ q_N,\ t\right)
\end{array}\right\}
\end{eqnarray*}
�����ŁC$i =\begin{array}{cccc}1,&2,&\ldots,&n\end{array}$�ł���D�S�������āC�^���G�l���M�[�Ɗ֘A���鑬�x�������v�Z���Ă����D$x$���������Ɍv�Z����ƁC
\begin{eqnarray*}
\dot{x}_i &=& \frac{dx_i}{dt} = \frac{d}{dt}\left\{x_i\left(q_1,\ q_2,\ \ldots ,\ q_N,\ t\right) \right\} \\
&=& \frac{\partial x_i}{\partial q_1}\frac{\partial q_1}{\partial t}+\frac{\partial x_i}{\partial q_2}\frac{\partial q_2}{\partial t}+\ldots +\frac{\partial x_i}{\partial q_k}\frac{\partial q_k}{\partial t} +\ldots+ \frac{\partial x_i}{\partial q_N}\frac{\partial q_N}{\partial t} + \frac{\partial x_i}{\partial t}\\
&=& \sum_{k=1}^{N}\frac{\partial x_i}{\partial q_k}\frac{\partial q_k}{\partial t}+\frac{\partial x_i}{\partial t} =\sum_{k=1}^{N}\frac{\partial x_i}{\partial q_k}\dot{q}_k + \frac{\partial x_i}{\partial t}
\end{eqnarray*}
���̎���$\dot{q}_k$�ŕΔ�������Ǝ��̊W����������D
\begin{eqnarray*}
\frac{\partial\dot{x}_i}{\partial\dot{q}_k} = \frac{\partial x_i}{\partial q_k}
\end{eqnarray*}
$y_i$�C$z_i$�ɑ��Ă����l�ȕό`���ł���̂ŁC$n$�̊e���_�̑��x�����͎��̂悤�ɕ\���ł��邱�ƂɂȂ�D
\begin{eqnarray*}
\left.\begin{array}{l}
\dot{x}_i = \displaystyle{\sum_{k=1}^{N}\frac{\partial x_i}{\partial q_k}\dot{q}_k + \frac{\partial x_i}{\partial t}} \\
\dot{y}_i = \displaystyle{\sum_{k=1}^{N}\frac{\partial y_i}{\partial q_k}\dot{q}_k + \frac{\partial y_i}{\partial t}} \\
\dot{z}_i = \displaystyle{\sum_{k=1}^{N}\frac{\partial z_i}{\partial q_k}\dot{q}_k + \frac{\partial z_i}{\partial t}}
\end{array}\right\}
\end{eqnarray*}
�X�ɁC�ނ荇����Ԃɂ�����d���̊T�O��������邽�߂ɁC���z�ψʂ����̈�ʍ��W�ŕ\�����Ă����D�����C���̂悤�ȊW�ƂȂ�D
\begin{eqnarray*}
\left.\begin{array}{l}
\delta x_i = \frac{\partial x_i}{\partial q_1}\delta q_1 + \frac{\partial x_i}{\partial q_2}\delta q_2 + \ldots + \frac{\partial x_i}{\partial q_N}\delta q_N = \displaystyle{\sum_{k=1}^{N}\frac{\partial x_i}{\partial q_k}\delta q_k } \\
\delta y_i = \displaystyle{\sum_{k=1}^{N}\frac{\partial y_i}{\partial q_k}\delta q_k } \\
\delta z_i = \displaystyle{\sum_{k=1}^{N}\frac{\partial z_i}{\partial q_k}\delta q_k }
\end{array}\right\}
\end{eqnarray*}
8.3 ��ʗ�
�@$N$���R�x�n��$n$�̓_�ɍ�p����̓x�N�g��
\begin{eqnarray*}
\mathbf{f}_i =X_i\mathbf{i} + Y_i\mathbf{j} + Z_i\mathbf{k} =\left[\begin{array}{ccc}X_i&Y_i&Z_i\end{array}\right]^T \quad (i=1,2,\ldots,n)
\end{eqnarray*}
���l���C�����̗͂ɂ�鉼�z�d��$\delta W$���l����D�����C�e��p�_�ɉ��z�ψ�
\begin{eqnarray*}
\delta\mathbf{r}_i = \left[\begin{array}{ccc}\delta x_i&\delta y_i& \delta z_i\end{array}\right]^T \quad (i=1,2,\ldots,n)
\end{eqnarray*}
���l����ƁC���z�d���́C�͂ƕψʂ̓��ςƂȂ�̂ŁC
\begin{eqnarray*}
\delta W &=& \sum_{i=1}^n \mathbf{f}\cdot\delta\mathbf{r}_i =\sum_{i=1}^n\left(X_i\delta x_i + Y_i\delta y_i + Z_i\delta z_i\right)=\sum_{i=1}^n\left(X_i\sum_{k=1}^{N}\frac{\partial x_i}{\partial q_k}\delta q_k+ Y_i\sum_{k=1}^{N}\frac{\partial y_i}{\partial q_k}\delta q_k+Z_i\sum_{k=1}^{N}\frac{\partial z_i}{\partial q_k}\delta q_k\right)\\
&=&\sum_{k=1}^{N}\sum_{i=1}^n\left(X_i\frac{\partial x_i}{\partial q_k}+ Y_i\frac{\partial y_i}{\partial q_k}k+Z_i\frac{\partial z_i}{\partial q_k}\right)\delta q_k \equiv \sum_{k=1}^{N}Q_k\delta q_k
\end{eqnarray*}
�̂悤�ɂ܂Ƃ߂邱�Ƃ��ł���̂ŁC
\begin{eqnarray*}
Q_k=\sum_{i=1}^n\left(X_i\frac{\partial x_i}{\partial q_k}+ Y_i\frac{\partial y_i}{\partial q_k}k+Z_i\frac{\partial z_i}{\partial q_k}\right)
\end{eqnarray*}
����ʍ��W�ɑΉ����Č����h��ʗ́h�Ƃ��Ē�`���邱�Ƃ��ł���D
8.4 �^���G�l���M�[�ɂ�����W
�@��ʍ��W�n�ŕ\�����ꂽ�^���G�l���M�[�Ɋւ���W���o���邽�߂ɁC�܂��C$n$�̎��_�ɑ��ăj���[�g���̑�Q�@�����l���C�����ɉ��z�ψʂ��|����Ƃ���������s���D�����C
$i=1,2,\ldots,n$�̂�����$i$�Ԗڂ̎���$m_i$�̎��_�̍��W�_$\mathbf{r}_i=[x_i,y_i,z_i]^T$�ƍ�p��$\mathbf{f}_i=[X_i,Y_i,Z_i]^T$�Ɋւ���W����
\begin{eqnarray*}
\left.\begin{array}{l}
\frac{d}{dt}\left(m_i\dot{x}_i\right)\delta x_i = X_i \delta x_i \\
\frac{d}{dt}\left(m_i\dot{y}_i\right)\delta y_i = Y_i \delta y_i \\
\frac{d}{dt}\left(m_i\dot{z}_i\right)\delta z_i = Z_i \delta z_i
\end{array}\right\}
\end{eqnarray*}
��P�����ӂ�ό`����D
\begin{eqnarray*}
\frac{d}{dt}\left(m_i\dot{x}_i\right)\delta x_i =\frac{d}{dt}\left(m_i\dot{x}_i\delta x_i\right)-m_i\dot{x}_i\delta\dot{x}_i
\end{eqnarray*}
�����ŁC
\begin{eqnarray*}
\delta\dot{x}_i =\frac{d}{dt}\left(\sum_{k=1}^{N}\frac{\partial x_i}{\partial q_k}\delta q_k \right) =\sum_{k=1}^{N}\left\{\frac{d}{dt}\left(\frac{\partial x_i}{\partial q_k} \right)\delta q_k+\frac{\partial x_i}{\partial q_k}\delta\dot{q}_k \right\} = \sum_{k=1}^{N}\left(\frac{\partial\dot{x}_i}{\partial q_k}\delta q_k + \frac{\partial x_i}{\partial q_k}\delta\dot{q}_k \right)
\end{eqnarray*}
����āC
\begin{eqnarray*}
\frac{d}{dt}\left(m_i\dot{x}_i\right)\delta x_i &=&\frac{d}{dt}\left(m_i\dot{x}_i\sum_{k=1}^{N}\frac{\partial x_i}{\partial q_k}\delta q_k\right)-m_i\dot{x}_i\sum_{k=1}^{N}\left(\frac{\partial\dot{x}_i}{\partial q_k}\delta q_k+\frac{\partial x_i}{\partial q_k}\delta\dot{q}_k \right) \\
&=& \sum_{k=1}^{N}\left\{ \frac{d}{dt}\left(m_i\dot{x}_i\frac{\partial\dot{x}_i}{\partial\dot{q}_k}\delta q_k\right)-m_i\dot{x}_i\left(\frac{\partial\dot{x}_i}{\partial q_k}\delta q_k+\frac{\partial \dot{x}_i}{\partial \dot{q}_k}\delta\dot{q}_k \right)\right\}\\
&=& \sum_{k=1}^{N}\left[ \frac{d}{dt}\left\{\frac{\partial}{\partial\dot{q}_k}\left(\frac{1}{2}m_i\dot{x}_i^2\right)\delta q_k\right\} - \frac{\partial}{\partial q_k}\left(\frac{1}{2}m_i\dot{x}_i^2\right)\delta q_k - \frac{\partial}{\partial\dot{q}_k}\left(\frac{1}{2}m_i\dot{x}_i^2\right)\delta\dot{q}_k\right] \\
&=& \sum_{k=1}^{N}\left[ \frac{d}{dt}\left\{\frac{\partial}{\partial\dot{q}_k}\left(\frac{1}{2}m_i\dot{x}_i^2\right)\right\}\delta q_k + \frac{\partial}{\partial\dot{q}_k}\left(\frac{1}{2}m_i\dot{x}_i^2\right)\delta\dot{q}_k - \frac{\partial}{\partial q_k}\left(\frac{1}{2}m_i\dot{x}_i^2\right)\delta q_k - \frac{\partial}{\partial\dot{q}_k}\left(\frac{1}{2}m_i\dot{x}_i^2\right)\delta\dot{q}_k\right] \\
&=& \sum_{k=1}^{N}\left[ \frac{d}{dt}\left\{\frac{\partial}{\partial\dot{q}_k}\left(\frac{1}{2}m_i\dot{x}_i^2\right)\right\} - \frac{\partial}{\partial q_k}\left(\frac{1}{2}m_i\dot{x}_i^2\right)\right]\delta q_k
\end{eqnarray*}
���ꂪ�C$X_i\delta x_i$�Ɠ������Ƃ����W��������D$y_i$�C$z_i$�Ɋւ��Ă����l�Ȃ̂ŁC������D
\begin{eqnarray*}
&& \frac{d}{dt}\left(m_i\dot{x}_i\right)\delta x_i = \sum_{k=1}^{N}\left[ \frac{d}{dt}\left\{\frac{\partial}{\partial\dot{q}_k}\left(\frac{1}{2}m_i\dot{x}_i^2\right)\right\} - \frac{\partial}{\partial q_k}\left(\frac{1}{2}m_i\dot{x}_i^2\right)\right]\delta q_k = X_i\delta x_i \\
&& \frac{d}{dt}\left(m_i\dot{y}_i\right)\delta y_i = \sum_{k=1}^{N}\left[ \frac{d}{dt}\left\{\frac{\partial}{\partial\dot{q}_k}\left(\frac{1}{2}m_i\dot{y}_i^2\right)\right\} - \frac{\partial}{\partial q_k}\left(\frac{1}{2}m_i\dot{y}_i^2\right)\right]\delta q_k = Y_i\delta y_i \\
&& \frac{d}{dt}\left(m_i\dot{z}_i\right)\delta z_i = \sum_{k=1}^{N}\left[ \frac{d}{dt}\left\{\frac{\partial}{\partial\dot{q}_k}\left(\frac{1}{2}m_i\dot{z}_i^2\right)\right\} - \frac{\partial}{\partial q_k}\left(\frac{1}{2}m_i\dot{z}_i^2\right)\right]\delta q_k = Z_i\delta z_i
\end{eqnarray*}
�����ŁC$n$�̎��_�ɑ��邱���̊W��S�ĉ����邱�Ƃɂ���D���̊W��
\begin{eqnarray*}
\sum_{i=1}^n\left\{\frac{d}{dt}\left(m_i\dot{x}_i\right)\delta x_i +\frac{d}{dt}\left(m_i\dot{y}_i\right)\delta y_i +\frac{d}{dt}\left(m_i\dot{z}_i\right)\delta z_i\right\}=\sum_{i=1}^n\left(X_i\delta x_i + Y_i\delta y_i + Z_i\delta z_i\right)
\end{eqnarray*}
�ƂȂ�C��̊W���ƈ�ʗ͂̒�`���玟����D
\begin{eqnarray*}
\sum_{i=1}^n\sum_{k=1}^N\left[\frac{d}{dt}\left\{\frac{\partial}{\partial\dot{q}_k}\left(\frac{1}{2}m_i\left[\dot{x}_i^2+\dot{y}_i^2+\dot{z}_i^2\right]\right)\right\} - \frac{\partial}{\partial q_k}\left\{\frac{1}{2}m_i\left(\dot{x}_i^2+\dot{y}_i^2+\dot{z}_i^2\right)\right\}\right]\delta q_k = \sum_{k=1}^NQ_k\delta q_k
\end{eqnarray*}
�ΏۂƂ���n�̉^���G�l���M�[$T$�͎��̂悤�ɕ\���ł���D
\begin{eqnarray*}
T = \sum_{i=1}^n\frac{1}{2}m_i\left(\dot{x}_i^2+\dot{y}_i^2+\dot{z}_i^2\right)
\end{eqnarray*}
�]���āC���̂悤�ȊW������܂�D
\begin{eqnarray*}
\sum_{k=1}^N\left\{\frac{d}{dt}\left(\frac{\partial T}{\partial\dot{q}_k}\right) - \frac{\partial T}{\partial q_k}\right\}\delta q_k = \sum_{k=1}^NQ_k\delta q_k
\end{eqnarray*}
$\delta q_k$�͔C�ӂɎ���̂ŁC���̊W���������邱�ƂɂȂ�D
\begin{eqnarray*}
\frac{d}{dt}\left(\frac{\partial T}{\partial\dot{q}_k}\right) - \frac{\partial T}{\partial q_k} = Q_k\quad\left(k=1,2,\ldots,N\right)
\end{eqnarray*}
��ʍ��W�ŕ\�����ꂽ�^���G�l���M�[$T$�ƈ�ʗ�$Q_k$�̊W��\���Ă���C�^���G�l���M�[�݂̂��l�����ꍇ��Lagrange�������ƌĂ��D
8.5 ���K
�P�D�}8-2�Ɏ����n�ɂ����āC�S�^���G�l���M�[�����߁C$x_1$�C$x_2$����ʍ��W�Ƃ��C�Ή������ʗ͂��`���āC�^���G�l���M�[�݂̂����܂�^����������Lagrange��������p���ċ��߂�D
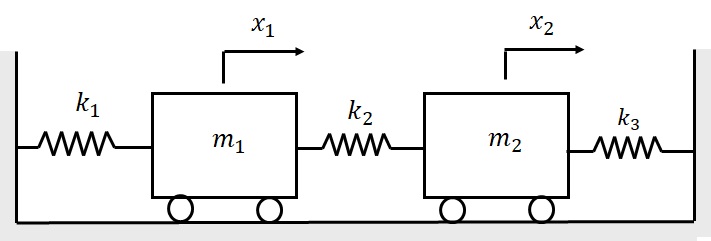
�}8-2�@�Q���R�x�n�U���n
�@
�Q�D�}8-3�Ɏ����悤�Ȍn�̏㉺���i�^���Ɩʓ��̉�]�^���ɑ���^�����l����D�Ԋu$l$�ŁC����$m$�̂R�̕��̂��Ȃ��ł���_�̎��ʂ͖����ł��C�d�S�ψʂ�$x$�C�d�S���̉�]��$\theta$�Ƃ��āC�n�S�̂̉^���G�l���M�[�����߁C�Ή������ʗ͂��`���āC�^���G�l���M�[�݂̂�p����Lagrange����������^�������������߂�D

�}8-3�@�W�����ʂ�z�����n�̏㉺-�s�b�`�U�����f��
�@
�R�D���̖₢�ɓ�����D
(1) �����ʓ����^�����鎿��$m$�̕��̂��l����D�ɍ��W�n$(r,\theta)$����ʍ��W�Ƃ��āC����$m$�̕��̂̉^���ɑ���Lagrange��������K�p���C�^�������������߂�D�����ŁC��ʗ͂�$Q_r(t)$�C$Q_\theta$�Ƃ���D
(2) $(x,y)$���W�n�ŕ\�����͂�$Q_x(t)$�C$Q_y(t)$�Ƃ���Ƃ��C��ʗ�$Q_r(t)$�C$Q_\theta$�Ƃ̊W�������D

�}8-4�@$(r,\theta)$���W�n�̎��_�̐U��
�@




