10.N自由度系の動力学,振動問題
10.1 回転と並進運動を伴う運動
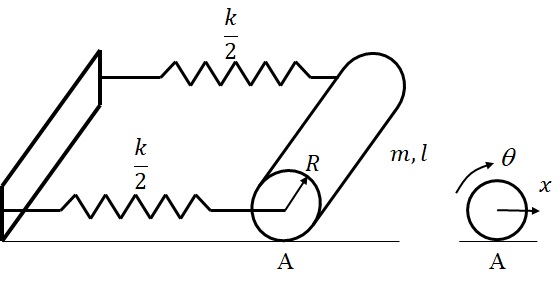
図10-1 円柱ローラーの運動
図10-1に示す両端の中心をばね支持されて平面上に置かれている一様な円柱ローラーの運動を考える.図に示すようにローラ中心(重心)の並進運動変位を$x$,回転角変位を$\theta$とし,2本のばね定数はそれぞれ$\frac{k}{2}$であり,ローラの質量を$m$,半径を$R$,長さを$l$とする.
ローラー中心軸回りの慣性モーメント$J_0$は,
\begin{eqnarray*}
J_0= \frac{1}{2}mR^2
\end{eqnarray*}
となるので,ローラーの並進運動と回転運動に基づく運動エネルギー$T$は次のようになる.
\begin{eqnarray*}
T = \frac{1}{2}m\dot{x}^2 + \frac{1}{2}J_0\dot{\theta}^2 = \frac{1}{2}m\dot{x}^2 + \frac{1}{2}\left(\frac{1}{2}mR^2\right)\dot{\theta}^2
\end{eqnarray*}
一方,ポテンシャルエネルギーは,ばねに蓄えられるエネルギーのみであるので次式となる.
\begin{eqnarray*}
U = \frac{1}{2}kx^2
\end{eqnarray*}
ここで,ローラーの接触点Aの条件について考える.
1) ローラーが面上をすべらず転がる場合
この場合,接触点Aに次のような拘束条件が成立することになる.
\begin{eqnarray*}
x = R\theta
\end{eqnarray*}
よって,ラグランジュ関数$L$は次のようになる.
\begin{eqnarray*}
L=T-U = \frac{1}{2}m\left(R\dot{\theta}\right)^2 + \frac{1}{2}\left(\frac{1}{2}mR^2\right)\dot{\theta}^2-\frac{1}{2}k\left(R\theta\right)^2
\end{eqnarray*}
一般座標を$\theta$とすることにより,ラグランジュ方程式は次式となる.
\begin{eqnarray*}
\frac{d}{dt}\left(\frac{\partial L}{\partial\dot{\theta}}\right) - \frac{\partial L}{\partial\theta} = 0
\end{eqnarray*}
ここで,
\begin{eqnarray*}
&& \frac{\partial L}{\partial\dot{\theta}}=\frac{3}{2}mR^2\dot{\theta}\text{ , }\frac{\partial L}{\partial\theta}=-kR\left(R\theta\right) \\
&& \frac{d}{dt}\left(\frac{3}{2}mR^2\dot{\theta}\right)+ kR^2\theta =0 \\
&& \therefore \frac{3}{2}mR~2\ddot{\theta} + kR^2\theta =0
\end{eqnarray*}
よって,この場合の運動方程式は次式となる.
\begin{eqnarray*}
\ddot{\theta} + \frac{2k}{3m}\theta =0
\end{eqnarray*}
2) ローラーが面上をすべる場合
この場合,接触点Aに発生する面と平行な方向の力(摩擦力)を定義する必要がある.
ここで,すべり量は,
\begin{eqnarray*}
s=x-R\theta
\end{eqnarray*}
であり,一般に摩擦力は,すべり速度$\dot{x}$の関数として定義される.摩擦力に対応する一般力を$f_s$とすると,対応する仮想変位は
\begin{eqnarray*}
\delta s=\delta x-R\delta\theta
\end{eqnarray*}
となるので,摩擦力による仮想仕事は次のようになる.
\begin{eqnarray*}
\delta W_s =f_s\delta s=f_x\delta x-Rf_x\delta\theta = \sum^kQ_k^(s)\delta q_k
\end{eqnarray*}
即ち,$x$,$\theta$を一般座標とすると,対応する一般力は
\begin{eqnarray*}
\left.\begin{array}{l}
Q_x = f_s \\
Q_\theta = -Rf_x
\end{array}\right\}
\end{eqnarray*}
この場合のラグランジュ関数は,
\begin{eqnarray*}
L=T-U = \frac{1}{2}m\dot{x}^2 + \frac{1}{2}\left(\frac{1}{2}mR^2\right)\dot{\theta}^2-\frac{1}{2}kx^2
\end{eqnarray*}
であり,
\begin{eqnarray*}
&& \frac{\partial L}{\partial\dot{x}}=m\dot{x}\text{ , }\frac{\partial L}{\partial x} = - kx\quad \therefore \frac{d}{dt}\left(m\dot{x}\right) + kx = f_s \\
&& \frac{\partial L}{\partial\dot{\theta}} = \frac{1}{2}mR^2\dot{\theta}\text{ , }\frac{\partial L}{\partial\theta}=0\quad \therefore \frac{d}{dt}\left(\frac{1}{2}mR^2\dot{\theta}\right) = -Rf_s
\end{eqnarray*}
よって,この場合の系の方程式は次のようになる.
\begin{eqnarray*}
\left.\begin{array}{l}
m\ddot{x} + kx = f_s \\
\frac{1}{2}mR^2\ddot{\theta} = -Rf_s
\end{array}\right\}
\end{eqnarray*}
10.2 一般座標の取り方
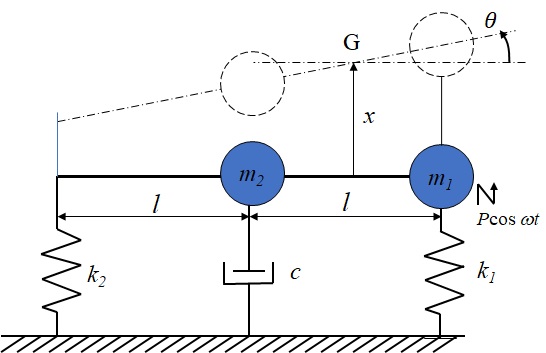
図10-2 質量の無視できる剛体棒で繋がれた2質点の運動
演習課題で考えた図10.2に示す,二つの質量$m_1$,$m_2$が質量の無視できる長さ$2l$の剛体棒に取付けられ一体となっている系の面内運動を考える.二つの質量は間隔$l$で取り付けられており,物体の両端である質量$m_1$の位置と剛体棒他端はそれぞればね定数$k_1$,$k_2$のばねで支持されている.また,質量$m_2$の位置は粘性減衰定数$c$のダッシュポットで支持されており,質量$m_1$の位置に振幅$P$ .角周波数$\omega$の周期的な強制加振力が作用している.この系の重心位置の上下方向変位を$x$,重心回りの回転角変位$\theta$を用いて,Lagrange方程式を用いて系の運動方程式を求める.ここで回転角変位は,反時計回りを正とする.
この系の重心位置は$m_2$の右方向に
\begin{eqnarray*}
l_{Gr}=\frac{m_1}{m_1+m_2}l
\end{eqnarray*}
$m_1$からだと左方向に
\begin{eqnarray*}
l_{Gl}=\frac{m_22}{m_1+m_2}l
\end{eqnarray*}
である.よって,この$l_{Gr}$,$l_{Gl}$を用いて,微小変形を仮定して,$m_1$と$m_2$の垂直方向変位を表わすと
\begin{eqnarray*}
&& m_1\text{: }x+l_{Gr}\sin\theta \fallingdotseq x + l_{Gr}\theta \\
&& m_2\text{: }x-l_{Gl}\sin\theta\fallingdotseq x-l_{Gl}\theta
\end{eqnarray*}
また,$k_2$部のばねの伸びは
\begin{eqnarray*}
x-\left(l+l_{Gl}\right)\sin\theta \fallingdotseq x - \left(l+l_{Gl}\right)\theta
\end{eqnarray*}
更に,全質量を$M=m_1+m_2$,重心回りの慣性モーメントを$I_G=m_1l_{Gr}^2+m_2l_{Gl}^2$と置くことにする.よって,この系の運動エネルギー$T$は,重心の並進運動と重心回りの回転運動の和となるので,次式となる.
\begin{eqnarray*}
T=\frac{1}{2}M\dot{x}^2 + \frac{1}{2}I_G\dot{\theta}^2
\end{eqnarray*}
一方,この系のポテンシャルエネルギー$U$は,
\begin{eqnarray*}
U=\frac{1}{2}k_1\left(x + l_{Gr}\theta\right)^2 + \frac{1}{2}k_2\left\{x + \left(l+l_{Gr}\right)\theta\right\}^2
\end{eqnarray*}
また,散逸関数$D$は,
\begin{eqnarray*}
D=\frac{1}{2}c\left\{\frac{d}{dt}\left(x - l_{Gl}\theta\right)\right\}^2 = \frac{1}{2}c\left(\dot{x}-l_{Gl}\dot{\theta}\right)^2
\end{eqnarray*}
ここで,ラグランジュ方程式は,$L=T-U$,$D$,一般座標$q_k$,一般力$Q_k$を用いて次式で表わされる.
\begin{eqnarray*}
\frac{d}{dt}\left(\frac{\partial L}{\partial\dot{q}_k}\right) - \frac{\partial L}{\partial q_k}+\frac{\partial D}{\partial\dot{q}_k} = Q_k
\end{eqnarray*}
よって,$q_1=x$,$q_2=\theta$と取ると,仮想仕事$\delta W$は,加振力$P\cos\omega t$が作用している場所の仮想変位が$\delta x + l_{Gr}\delta\theta$となるので,
\begin{eqnarray*}
\delta W = P\cos\omega t\times\left(\delta x + l_{Gr}\delta\theta\right) = Q_x\delta x + Q_\theta\delta \theta
\end{eqnarray*}
のように表すことができる.よって,
\begin{eqnarray*}
\frac{\partial L}{\partial\dot{x}}=M\dot{x}\text{ , }\frac{\partial L}{\partial x}= -k_1\left(x+l_{Gr}\theta\right)-k_2\left\{x-\left(l+l_{Gl}\right)\theta\right\}\text{ , }\frac{\partial D}{\partial\dot{x}}=c\left(\dot{x}-l_{Gl}\dot{\theta}\right)
\end{eqnarray*}
より
\begin{eqnarray*}
&& \frac{d}{dt}\left(M\dot{x}\right) + k_1\left(x+l_{Gr}\theta\right) + k_2\left\{x-\left(l+l_{Gl}\right)\theta\right\} + c\left(\dot{x}-l_{Gl}\dot{\theta}\right) = P\cos\omega t \\
&& \therefore M\ddot{x} + c\dot{x} -cl_{Gl}\dot{\theta} + \left(k_1+k_2\right)x + \left\{k_1l_{Gr}-k_2\left(l+l_{Gl}\right)\right\}\theta = P\cos\omega t
\end{eqnarray*}
同様に,
\begin{eqnarray*}
\frac{\partial L}{\partial\dot{\theta}}=I_G\dot{\theta}\text{ , }\frac{\partial L}{\partial\theta}= -k_1l_{Gr}\left(x+l_{Gr}\theta\right)+k_2\left(l+l_{Gr}\right)\left\{x-\left(l+l_{Gl}\right)\theta\right\}\text{ , }\frac{\partial D}{\partial\dot{\theta}}=-cl_{Gl}\left(\dot{x}-l_{Gl}\dot{\theta}\right)
\end{eqnarray*}
より
\begin{eqnarray*}
&& \frac{d}{dt}\left(I_G\dot{\theta}\right) + k_1l_{Gr}\left(x+l_{Gr}\theta\right) - k_2\left(l+l_{Gr}\right)\left\{x-\left(l+l_{Gl}\right)\theta\right\} - cl_{Gl}\left(\dot{x}-l_{Gl}\dot{\theta}\right) = l_{Gr}P\cos\omega t \\
&& \therefore I_G\ddot{\theta} - cl_{Gl}\dot{x} + cl_{Gl}^2\dot{\theta} + \left\{k_1l_{Gr} - k_2\left(l+l_{Gr}\right)\right\}x + \left\{k_1l_{Gr}^2 + k_2\left(l+l_{Gl}\right)^2\right\}\theta = l_{Gr}P\cos\omega t
\end{eqnarray*}
10.3 演習
図10.3に示すように,質量$m$,半径$r$円柱が半径𝑅の円筒面を持つ質量$M$の台上をすべらず右図のようにころがり振動する.台はばね定数$k$で他端を支持されており,滑らかに水平面内を動くことができる.
(1) 運動エネルギー$T$を求めよ.
(2) ポテンシャルエネルギー$U$を求めよ.
(3) Lagrange方程式を用いて運動方程式を導出せよ.
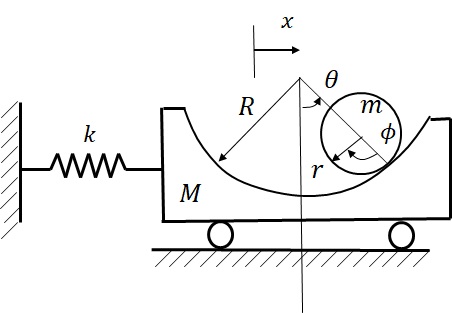
図10-3 円筒面を転がる円柱と台の運動



