11�D�A���̂̐U�����T�i���̉��U���j
�@����܂ł̃��f�����ɂ����ẮC�}11-1�Ɏ����悤�ɁC���z���Ă��鎿�ʂ���_�ɏW�����Ă��鉼�肵�āC���̎��ʂƂ˂̃��f���ŐU�������l���Ă����D�}(a)�ł́C�_�̎������̐U����_�̐�[�Ɏ��ʂ�����Ɖ��肵�Ē�܂�h�������ʁh�Ɩ_�̎������̍����ɂ���܂铙���˒萔���߁C�P���R�x�U���n���f�����l����D�܂��C�}(b)�̂悤�ɁC���ʂ𗣎U�I�ɂQ�_�ɐU�蕪���C���̊Ԃ��˓��������v�f�ő����R�x�i�����ł͂Q���R�x�j�n�Ń��f�������邱�Ƃ��l�����D�������Ȃ���C�K�������W�����ʂɒu����������C�����˂Ōq���悤�ȃ��f���ōl���Ȃ���Ȃ�Ȃ��킯�ł͂Ȃ��C�Ώۂɉ����ẮC���z�����l�q�����̂܂ܕ�����悤�ȃ��f�����������������ۂ𗝉����Ղ��ꍇ������D�����ł́C���z���ʌn�ɕ��ނ�����{�I�ȃ��f�����Љ��D
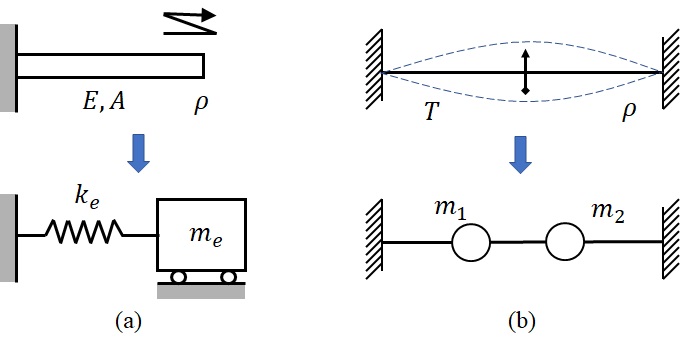
�}11-1�@�W�����ʌn�ւ̃��f����
�@
11.1 ���̉^��������
�@�}11-1(b)�̏㑤�Ɏ������悤�ɒ��������ɔg���`���悤�ɏ㉺����悤�ȐU���������n�́C�h�����f���h�Ƃ��āC���f�������邱�Ƃ��ł���D�����f���ł́C�����x$\rho_L$�ƒ���$T$��^���C���z�������ʂƒ��͂̑��ݍ�p�ŐU�����錻�ۂ��l����D�}11-2�Ɏ����悤�Ɍ��̒���������$x$���W�����C���̒�������������Ɍ��̉��i���݁j�ψʂ�$y$�Ƃ���D���̉��ψ�$y$�́C���ԓI�ɕω�����Ƌ��ɁC$x$�����ɕ��z����̂ŁC�}11-2�Ɏ����悤�ɁC����$t$��$x$���W�̊�$y=y(x,t)$�̌`���ŕ\���ł���D���̂Ƃ�����$T$�͕ω����Ȃ��Ɖ��肷��D
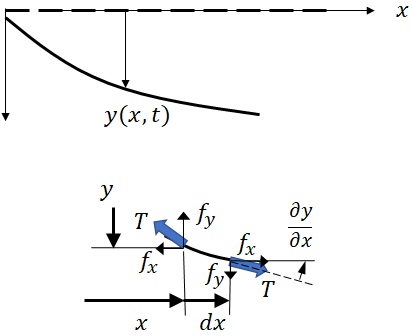
�}11-2�@�����f��
�@
�^���������̓��o�ɍۂ��ẮC�}�Ɏ����悤�Ɂh����ʒu$x$�i�C�Ӂj�ɂ������������$dx$�����o���C���̔��������̗��[�ɔ�������͂��l����D���������̍����ł���$x$�̈ʒu�̉��ψʂ�$y(x,t)$�ł���C�E���͔������������W�������̂�$y(x+dx,t)$�ƂȂ�D�܂��C�}�Ɏ��������v�f���[�̒���$T$�������Ɉ��������ƂȂ����E�̊p�x�����ꂼ��$\theta_1$�C$\theta_2$�Ƃ����
\begin{eqnarray*}
&& \tan\theta_1=\frac{\partial y(x,t)}{\partial x}\\
&& \tan\theta_2=\frac{\partial y(x+dx,t)}{\partial x}
\end{eqnarray*}
�ł���C$\theta_1\ll 1$�C$\theta_2\ll 1$�Ƃ����
\begin{eqnarray*}
&& \tan\theta_1\approx\theta_1=\frac{\partial y(x,t)}{\partial x}\\
&& \tan\theta_2\approx\theta_2=\frac{\partial y(x+dx,t)}{\partial x}
\end{eqnarray*}
���̗��[�ɔ�������㉺�����̗�$f_y(x,t)$�C$f_x(x,t)$���l����ƁC�����v�f���[�ɔ������钣��$T$��$x$�����C$y$�����̕��͂��l����Ηǂ��̂ŁC�����̂悤�ɕ\�킷���Ƃ��ł���D
\begin{eqnarray*}
\left.\begin{array}{l}
f_x(x,t) = - T\cos\theta_1= -T\cos\frac{\partial y(x,t)}{\partial x} \approx - T \\
f_y(x,t) = - T\sin\theta_1= -T\sin\frac{\partial y(x,t)}{\partial x} \approx -T\frac{\partial y(x,t)}{\partial x}
\end{array}\right\}
\end{eqnarray*}
\begin{eqnarray*}
\left.\begin{array}{l}
f_x(x+dx,t) = T\cos\theta_2=T\cos\frac{\partial y(x+dx,t)}{\partial x} \approx T\\
f_y(x+dx,t) = T\sin\theta_2=T\sin\frac{\partial y(x+dx,t)}{\partial x} \approx T\frac{\partial y(x+dx,t)}{\partial x}
\end{array}\right\}
\end{eqnarray*}
����āC�����v�f�ɑ��鐅�������̂��ׂĂ̍�p�̘͂a��
\begin{eqnarray*}
-f_x(x,t) + f_x(x+dx,t) = -T + T =0
\end{eqnarray*}
�ƂȂ�̂ŁC���������ɂ͉^�����Ȃ����Ƃ�������D�����v�f�̉��������̉^���Ɋւ���Newton�̑�Q�@�����l�����
\begin{eqnarray*}
\rho_Ldx\frac{\partial^2y(x,t)}{\partial t^2} = -f_y(x,t) + f_y(x+dx,t) = -T\frac{\partial y(x,t)}{\partial x} + T\frac{\partial y(x+dx,t)}{\partial x}
\end{eqnarray*}
�ƂȂ�D�����ŁC�E�ӑ�Q����$\frac{\partial y(x+dx,t)}{\partial x}$��Taylor�W�J�����
\begin{eqnarray*}
\rho_Ldx\frac{\partial^2y(x,t)}{\partial t^2} = -T\frac{\partial y(x,t)}{\partial x} + T\left\{\frac{\partial y(x,t)}{\partial x}+\frac{dx}{1!}\frac{\partial^2 y(x,t)}{\partial x^2} + \frac{dx^2}{2!}\frac{\partial^3 y(x,t)}{\partial x^3} + \ldots \right\}
\end{eqnarray*}
����āC$dx\ll 1$���C������D
\begin{eqnarray*}
\rho_Ldx\frac{\partial^2y(x,t)}{\partial t^2} = Tdx\frac{\partial^2 y(x,t)}{\partial x^2}
\end{eqnarray*}
\begin{eqnarray*}
\therefore \rho_L\frac{\partial^2y(x,t)}{\partial t^2} = T\frac{\partial^2 y(x,t)}{\partial x^2}
\end{eqnarray*}
$x$��$t$�̊��ɂȂ�͎̂����ł���̂ŁC�\�L���ȗ�����Ǝ��̂悤�ȉ^������������܂�D
\begin{eqnarray*}
&& \frac{\partial^2y}{\partial t^2} = c^2\frac{\partial^2 y}{\partial x^2} \\
&& c=\sqrt{\frac{T}{\rho_L}}
\end{eqnarray*}
���̉^���������́C�ꎟ���̔g���������C���邢�́C�Q�K�̐��`�Δ����������C���邢�́C�o�Ȍ^�Δ����������ƌĂ��`���ƂȂ�D
11.2 ���̋K���U��
��������P��̊p�U����$\omega_n$�ŐU������ꍇ���l����D�g���������ŋL�q������Ԃɂ����ẮC��ʂɔg���i�s�����ɓ`�d�i�i�s�g�j������C�t�����ɓ`�d�i��ޔg�j����g�����ۂ�����邪�C�U���`�ԁi���[�h�j����̂����ꍇ�ɂ́C���ꂪ��ݔg�ƂȂ邽�߁C��ԂɊւ���ϓ��Ǝ��ԓI�ȕϓ������čl���邱�Ƃ��ł���D���̂悤�ȐU���́C�K���U���ƌĂ�C$y(x,t)$�����̂悤�ɒu�����Ƃ��ł���D
\begin{eqnarray*}
y\left(x,t\right) = Y_n(x)e^{i\omega_nt}
\end{eqnarray*}
�����ŁC$Y_n(x)$�́C$x$�������ɕ��z����U���ω��i�U�����z���j��\���Ă���C���̂悤�ȐU�����z�ɂȂ�Ƃ��̊p�U������$\omega_n$�Ƃ������ƂɂȂ�D���̎����^���������ɑ�����Đ�������D
\begin{eqnarray*}
&& -\omega_n^2Y_n(x) = c^2\frac{d^2Y(x)}{dx^2} \\
&& \therefore \frac{d^2Y(x)}{dx^2}+\frac{\omega_n^2}{c^2}Y_n(x) = 0
\end{eqnarray*}
����āC$\omega_n$���m�肳���C���̎���$Y(x)$�Ɋւ���萔�W���̐��`������������ƂȂ�̂ŁC��������$\lambda$�Ƃ��āC$Y_n(x)=Ye^{\lambda x}$�������āC���������������߂�D
\begin{eqnarray*}
\left(\lambda^2+\frac{\omega_n^2}{c^2}\right)=0
\end{eqnarray*}
����āC�������́C
\begin{eqnarray*}
\lambda = \pm i\frac{\omega_n}{c}
\end{eqnarray*}
�ƂȂ�̂ŁC$Y_n(x)$�͎����ƂȂ�D
\begin{eqnarray*}
Y(x) &=& a_1e^{i\frac{\omega_n}{c}x} + b_1e^{-i\frac{\omega_n}{c}x} \\
&=& Y_1\cos\frac{\omega_n}{c}x + Y_2\sin\frac{\omega_n}{c}x
\end{eqnarray*}
�ȏォ��C�����P�ꃂ�[�h�ŐU���i�K���U���j����Ƃ��C$Y_1$�C$Y_2$��C�Ӓ萔�Ƃ��Ď��̂悤�ȐU�����������l���邱�Ƃ��ł���D
\begin{eqnarray*}
y\left(x,t\right) =\left(Y_1\cos\frac{\omega_n}{c}x + Y_2\sin\frac{\omega_n}{c}x\right)e^{i\omega_nt}
\end{eqnarray*}
11.3 �ŗL�U�����ƌŗL���[�h
�@���̉^���������͔����v�f�ɂ�����^�����L�q���Ă�����̂ŁC�K���U�������肵�ďo�Ă������́C�C�ӂ̈ʒu$x$�̂��鎞��$t$�i�C�Ӂj�̉^����\�����Ă���D�����ŁC���̒������l���āC���̗��[�̏������߁C���̎��̊W���߂邱�Ƃɂ���D���̒�����$l$�Ƃ��āC���̗��[�̍��W�ʒu$x=0$�C$x=l$�̏����C���Ȃ킿�C���E�������߂邱�Ƃɂ���D
���[�Œ�
�}10-1(b)�̏㑤�̐}�Ŏ������悤�ȗ��[���Œ�i�S���j����Ă���ꍇ���l����D���̏ꍇ�̏����́C
\begin{eqnarray*}
y\left(0,t\right) = y\left(l,t\right) = 0
\end{eqnarray*}
�ƂȂ�̂ŁC�C�ӂ̎����ɂ����āC
\begin{eqnarray*}
Y\left(0\right) = Y\left(l\right) = 0
\end{eqnarray*}
�ƂȂ邱�Ƃ��K�v�ƂȂ�D�����C
\begin{eqnarray*}
&& Y\left(0\right) = Y_1\cos(0) + Y_2\sin(0)= Y_1 =0\\
&& Y\left(l\right) = Y_1\cos\frac{\omega_n}{c}l + Y_2\sin\frac{\omega_n}{c}l =Y_2\sin\frac{\omega_n}{c}l = 0
\end{eqnarray*}
$Y_2$�́C�ǂ�Ȓl����蓾��C�Ӓ萔�Ȃ̂ŁC���̊W����܂�D
\begin{eqnarray*}
\sin\frac{\omega_n}{c}l = 0
\end{eqnarray*}
���̂悤�ɁC�K���U���ɑ��āC���E������^���邱�Ƃɂ���܂�W���́C�U�����������ƌĂ�C�K���U���̌ŗL�U�����ƌŗL���[�h�����肷��W���ƂȂ�D�����C$\sin$����ƂȂ�����ɂ��C�U�����������̉��͎��̂悤�ɂȂ�D
\begin{eqnarray*}
\frac{\omega_n}{c}l = n\pi (n=1,2,\ldots,)
\end{eqnarray*}
�����C�U������������������͖�����܂�D�܂����̊W������C�K���U���̊p�U�����́C
\begin{eqnarray*}
\omega_n = \frac{n\pi}{l}c = \frac{n\pi}{l}\sqrt{\frac{T}{\rho}}
\end{eqnarray*}
�̊W���Œ�܂邱�ƂɂȂ�D$n$�̒l�ɂ��C��є�т̒l�ƂȂ邪�C�K���U����U�����K�肷��U�����ł���C��$n$���̌ŗL�p�U�����ƌĂ��D���̒l����܂��$x$�������ɕ��z����U����$Y_n(x)$�͎��̂悤�ɂȂ�D
\begin{eqnarray*}
Y_n(x) = Y_2\sin\frac{\omega_n}{c}x = Y_2\sin\frac{n\pi}{l}x
\end{eqnarray*}
����āC�ő�U�����P�ƂȂ�悤��$Y_2=1$�Ƃ��āC��$n$�̐��K���Ƃ��Ď��̂悤�ɒ�߂邱�Ƃ��ł���D
\begin{eqnarray*}
Y_n(x) = \sin\frac{n\pi}{l}x
\end{eqnarray*}
���̂悤�ɂ��Ē�܂�U�����z���́C�ŗL���[�h���ƌĂ�ŗL�p�U����$\omega_n$�ɑΉ����Ē�܂�D�ŗL�U�����ŐU�����Ă��鎞�̋�ԓI�ȐU���`�Ԃ�\�����邱�ƂɂȂ�D���̍�����������[�Œ�̏ꍇ�̐U�����[�h��}11-3�Ɏ����D
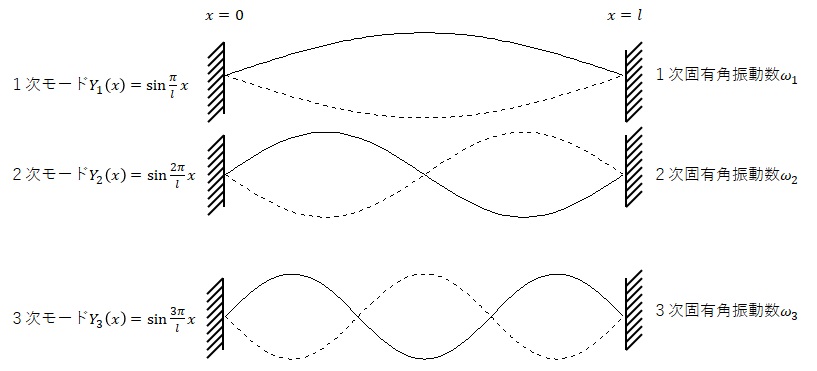
�}11-3�@���[���Œ肳�ꂽ���̂P������R���܂ł̌ŗL�i�U���j���[�h
�@
11.4 ���̎��R�U��
�Q���R�x�U���n����̗ސ��ŕ�����Ǝv���邪�C���̂悤�ɌŗL�p�U��������������悤�Ȍn�ł́C�����̂ǂ̐U�����ł��U������\��������̂ŁC�ŗL�p�U�����ƌŗL���[�h�ŕ\������邷�ׂĂ̋K���U���̏d�ˍ��킹�Ƃ��Ď��R�U���������ƍl����D�����C���R�U�������̈�ʉ��́C����W����$\alpha_n$�Ƃ��āC���̂悤�ɕ\�������D
\begin{eqnarray*}
y\left(x,t\right) = \sum_{n=1}^{\infty}Y_n(x)\alpha_ne^{i \omega_nt}
\end{eqnarray*}
���E�������^������ƁC�ŗL�p�U����$\omega_n$�ƌŗL���[�h��$Y_n(x)$����܂�D����ɁC����������^���邱�Ƃɂ���āC$\alpha_n$���߂邱�ƂɂȂ邪�C����$\alpha_n$�́C���f�U���ł���̂ŁC�����C�����ɑΉ�����Q�̖��m�������߂�K�v������D���[�Œ�̋��E�����ł́C$Y_n(x)=\sin\frac{n\pi}{l}x$�ƂȂ�̂ŁC���̂悤�ɕ\�����Ƃ��ł���D
\begin{eqnarray*}
y\left(x,t\right) = \sum_{n=1}^{\infty}\sin\frac{n\pi}{l}x\alpha_ne^{i \omega_nt}=\sum_{n=1}^{\infty}\sin\frac{n\pi}{l}x\left(A_n\cos\omega_nt+B_n\sin\omega_nt\right)
\end{eqnarray*}
���m�����Q�ɂȂ�̂́C����܂œ��l�C$t=0$�̎��̒l�Ƃ��̈����������l�̂Q��^���Ȃ��ƁC�n�̉^����Ԃ����߂邱�Ƃ��ł��Ȃ��Ƃ��������������̊K���i��K�j�ɂ����̂ł���D����āC���Ԕ��������߂��
\begin{eqnarray*}
\dot{y}\left(x,t\right) = \sum_{n=1}^{\infty}\sin\frac{n\pi}{l}x\omega_n\left(-A_n\sin\omega_nt+B_n\cos\omega_nt\right)
\end{eqnarray*}
�ƂȂ�D$y$�C$\dot{y}$�Ƃ�$t=0$�̎��C���W�n$x$�̊��ƂȂ�̂ŁC���������Ƃ��ẮC���ꂼ��$x$�̊��Ƃ��āC�����ψʕ��z$f(x)$�Ə������x���z$g(x)$��^����K�v�����鎖��������D
�����C���������͎��̂悤�ɗ^�����邱�ƂɂȂ�D
\begin{eqnarray*}
&& y\left(x,0\right) = \sum_{n=1}^{\infty}A_n\sin\frac{n\pi}{l}x = f(x) \\
&& \dot{y}\left(x,0\right) =\sum_{n=1}^{\infty}B_n\omega_n\sin\frac{n\pi}{l}x = g(x)
\end{eqnarray*}
$A_n$�C$B_n$�����߂邽�߂ɁC���̂悤�Ȑ��K���̒��𐫂𗘗p����D
\begin{eqnarray*}
\int_0^l\sin\frac{n\pi}{l}x\sin\frac{m\pi}{l}xdx &=& \frac{1}{2}\int_0^l\left\{\cos\frac{(n-m)\pi}{l}x-\cos\frac{(n+m)\pi}{l}x\right\}dx \\
&=& \frac{1}{2}\left[\frac{l}{(n-m)\pi}\sin\frac{(n-m)\pi}{l}x - \frac{l}{(n+m)\pi}\sin\frac{(n+m)\pi}{l}x\right]0^l \\
&=& \frac{l}{2}\left[\frac{\sin(n-m)\pi}{(n-m)\pi}\right] = \left\{\begin{array}{ll}
\frac{l}{2} & (n=m) \\
0 & (n\neq m) \end{array}\right.
\end{eqnarray*}
�����C����������\�킷�W����$\sin\frac{m\pi}{l}x$���|���C$x$�Ɋւ��āC$0$����$l$�܂Őϕ�����ƁC$\sum_{n=1}^{\infty}$�̒��̊Y�����鍀$m=n$�̍��݂̂��l����邱�ƂɂȂ�̂ŁC�����Ɏ����W������܂�D
\begin{eqnarray*}
&& A_n=\frac{2}{l}\int_0^lf(x)\sin\frac{n\pi}{l}xdx \\
&& B_n=\frac{2}{l\omega_n}\int_0^lg(x)\sin\frac{n\pi}{l}xdx
\end{eqnarray*}
11.5 ���K
(1) ���[�Œ�C����$l$�̌���ލ��ʒu���������C�������`$4y_0x\left(l-x\right)/l^2$�ɕۂD$t=0$�ɂ����ēˑR��������R�ɂ����Ƃ���ƌ��̐U���͂ǂ̂悤�ɂȂ邩�D
(2) ���}�Ɏ����悤�ɁC����$l$�̌��̒[����$s$�̈ʒu�ŁC$a$�̂���݂�^���ĕ������D���̎��R�U���������߂�D
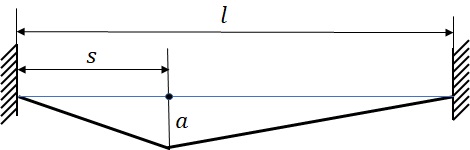
�}11-4�@���̎��R�U��
�@
(3) ���ȏ�170�y�[�W�ŏq�ׂ��Ă���悤�ɁC�g��������
\begin{eqnarray*}
\frac{\partial^2y}{\partial t^2} = c^2\frac{\partial^2y}{\partial x^2}
\end{eqnarray*}
�ɑ����ʉ��́C$f_1$�C$f_2$��C�ӂ̊��Ƃ��āC
\begin{eqnarray*}
y=f_1\left(x-ct\right)+f_2\left(x+ct\right)
\end{eqnarray*}
�̌`���ŗ^������D�㎮���g�������������邱�Ƃ������Ȃ����D
(4) �����x$\rho=3.36\times10^{-3}$kg/m�C����$T=1100$N�̃M�^�[�̑�T���̉��g�̑��x�����߂�D�������i��U���j�ƍׂ����i��P���j�Ƃł͂ǂ���̉��g���������D




