12�D�A���̂̐U�����U�i�_�̏c�U���j
12.1 �A���̂ɂ�����͂ƕό`�̋L�q
�@�}12-1�Ɏ����悤�Ƀf�J���g���W�n$xyz$���߁C�Ώە��̂̔C�ӈʒu$\left(x,y,z\right)$�ɂ����āC$xyz$�e�������ɂ��ꂼ��$dx$�C$dy$�C$dz$�̔����ȕӂŌ`������钼���̂��l����D�����̂̌������������ʂ͊e���ɑ��Đ����ł���C�e�Ζʂ͐}�Ɏ����悤�ɁC���̎������ɕӂ̒������������W�_���ω�����D
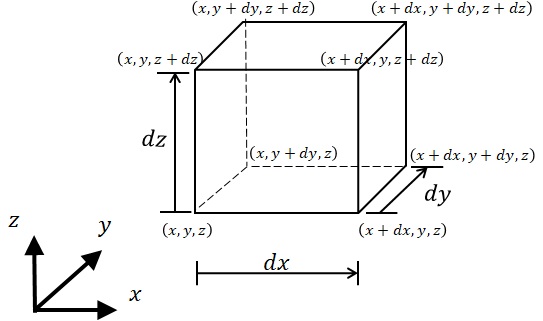
�}12-1�@���̂̔C�ӓ_�ʒu�̔����v�f
�@
�@���̒����̔����v�f�ɍ�p����͂��l���C�^���������o���邱�Ƃ��l����D�}12-2�Ɏ����悤�ɁC��p�͂Ƃ��āC$x$���ɐ����͂Q�̖ʂɁC�ʂɐ����ɓ����P�ʖʐϓ�����̗́i���́j$\sigma_{xx}$�Ɩʂƕ��s�ɁC$y$���C�y�сC$z$�������ɓ����P�ʖʐϓ�����̗́i���́j$\tau_{xy}$�C$\tau_{xz}$�����ŕ\�������悤�ɑ傫���ƕ������l���邱�Ƃ��ł��C$x$���W��$x+dx$�̖ʂɓ����͂��e�������Ɠ��������Ƃ���ƁC�ÓI�Ȓނ荇����Ԃɂ����ẮC�����̗͂ƒނ荇���͂�������ʂœ����ƍl������̂ŁC�������t�̓��l�̒P�ʖʐϓ�����̗́i���́j���l���邱�Ƃ��ł���D$y$���C$z$���ɐ����ȑ�����Q�̖ʂɂ��Ă����l�ł���C$z$���ɐ����ȂQ�̖ʂɓ����P�ʖʐϓ�����̗́i���́j�Ɋւ��Ă͐ԐF�̖��̂悤�ɁC�ʂɐ����ȉ���$\sigma_{zz}$�C�ʂɕ��s��$x$���C$y$�������̉���$\tau_{zx}$�C$\tau_{zy}$���l���邱�Ƃ��ł���D�܂��}���ɂ͎����Ă��Ȃ����C$y$���ɐ����ȂQ�̖ʂɓ����P�ʖʐϓ�����̗́i���́j�́C�ʂɐ����ȉ���$\sigma_{yy}$�C�ʂɕ��s��$z$���C$x$�������̉���$\tau_{yz}$�C$\tau_{yx}$���l���邱�Ƃ��ł���D
�@�����̂ɍ�p����͂́C�e���͂��`�����ʂ̖ʐς��������l�ł���C���̕����͖��̕����ƑΉ�����D�����ŁC�_$\left(x,y,z\right)$�Ɠ_$\left(x,y+dy,z\right)$��ʂ�$y$�����̃��[�����g�l����ƁC�r�̒�����$dx$��$z$�������̗�$\tau_{zx}dydz$�Ƙr�̒�����$dz$��$x$�������̗�$\tau_{zx}dxdy$�̂Q�̃��[�����g�����݂��C���ꂼ��$y$�������ɑ��āC�����i�������j�ƉE���̋t�����ƂȂ�̂ŁC�ÓI�Ȓނ荇����Ԃł��̒����̂���]���Ȃ��ƍl����Ǝ��̊W�����藧���ƂɂȂ�D
\begin{eqnarray*}
&& - dx\times\tau_{xz}dydz + dz\times\tau_{zx}dxdy = 0 \\
&& \left(-\tau_{xz} + \tau_{zx}\right)dxdydz = 0 \\
&& \therefore -\tau_{xz} + \tau_{zx} = 0
\end{eqnarray*}
���l�ɁC�ÓI�Ȓނ荇����Ԃ�$x$���C$z$�����̃��[�����g�̒ލ������l����ƁC���̊W����܂�D
\begin{eqnarray*}
\left.\begin{array}{l}
\tau_{xy} = \tau_{yx} \\
\tau_{yz} = \tau_{zy} \\
\tau_{zx} = \tau_{xz}
\end{array}\right\}
\end{eqnarray*}
����āC$dxdydz\longrightarrow 0$���l����ƕ��̂̔C�ӂ̈ʒu$\left(x,y,z\right)$�ɂ����Ď��̂悤�ȉ��͂̑g�i���̓e���\���j���`���邱�Ƃ��ł���D
\begin{eqnarray*}
\left[\begin{array}{ccc}
\sigma_{xx} & \tau_{xy} & \tau_{zx} \\
\tau_{xy} & \sigma_{yy} & \tau_{yz} \\
\tau_{zx} & \tau_{yz} & \sigma_{zz}
\end{array}\right]
\end{eqnarray*}
�����C�����v�f�ōl������͂Ƃ��āC�ʂɍ�p����́F�P�ʖʐϓ�����̗͂ł��鉞�͂��`����D�����ł͐������ȗ����邪�C���̓e���\���̊e�����̍�p�ɑΉ����Ĕ�������ό`��P�ʒ����ӂ�̕ψʂł���c�����Œ�`���C���l�̑Ή�����c�e���\�������̂悤�ɒ�`���邱�Ƃ��ł���D
\begin{eqnarray*}
\left[\begin{array}{ccc}
\varepsilon_{xx} & \gamma_{xy} & \gamma_{zx} \\
\gamma_{xy} & \varepsilon_{yy} & \gamma_{yz} \\
\gamma_{zx} & \gamma_{yz} & \varepsilon_{zz}
\end{array}\right]
\end{eqnarray*}
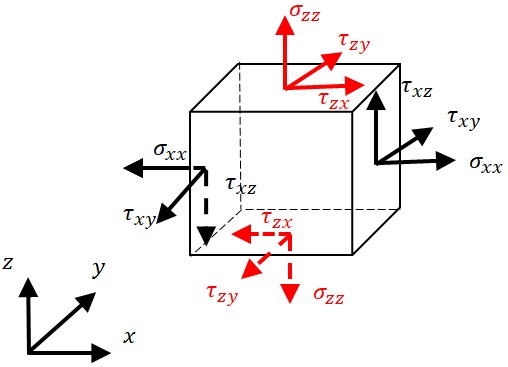
�}12-2�@�����̔����v�f�̊e�ʂɍ�p����́i���́j
�@
�@�����v�f�����̂őz�肳����p�͂ɂ��Ă���ɍl����D�e���͐����́C�ʒu$\left(x,y,z\right)$�Ǝ���$t$�ɑ��ĕω�����̂ŁC������Ɨ��ϐ��Ƃ�����ƍl���邱�Ƃ��ł���D�����v�f�����̂�$x$�������ɍ�p����͐����Ƃ��āC$x$���Ȑ����Ȗʂɂ����āC$\sigma_{xx}(x+dx,y,z,t)$��$\sigma_{xx}(x,y,z,t)$�C$y$���ɐ����Ȗʂɂ�����$\tau_{xy}(x,y+dy,z,t)$�C$\tau_{xy}(x,y,z,t)$�C$z$���ɐ����Ȗʂɂ�����$\tau_{zx}(x,y,z+dz,t)$��$\tau_{zx}(x,y,z,t)$�e�Ζʂɑ��݂���D�����ŁCTaylor�W�J��p�����
\begin{eqnarray*}
\left.\begin{array}{l}
\sigma_{xx}(x+dx,y,z,t) = \sigma_{xx}(x,y,z,t) + \frac{\partial\sigma_{xx}}{\partial x}dx + \frac{1}{2!}\frac{\partial^2\sigma_{xx}}{\partial x^2}dx^2 + \ldots\\
\tau_{xy}(x,y+dy,z,t) = \tau_{xy}(x,y,z,t) + \frac{\partial\tau_{xy}}{\partial y}dy + \frac{1}{2!}\frac{\partial^2\tau_{xy}}{\partial y^2}dy^2 + \ldots \\
\tau_{zx}(x,y,z+dz,t) = \tau_{zx}(x,y,z,t) + \frac{\partial\tau_{zx}}{\partial z}dz + \frac{1}{2!}\frac{\partial^2\tau_{zx}}{\partial z^2}dz^2 + \ldots
\end{array}\right\}
\end{eqnarray*}
�ƂȂ�̂ŁC$dx$�C$dy$�C$dz$�̊e1�����݂̂��l�������
\begin{eqnarray*}
\left.\begin{array}{l}
\sigma_{xx}(x+dx,y,z,t) \fallingdotseq \sigma_{xx}(x,y,z,t) + \frac{\partial\sigma_{xx}}{\partial x}dx \\
\tau_{xy}(x,y+dy,z,t) \fallingdotseq \tau_{xy}(x,y,z,t) + \frac{\partial\tau_{xy}}{\partial y}dy \\
\tau_{zx}(x,y,z+dz,t) \fallingdotseq \tau_{zx}(x,y,z,t) + \frac{\partial\tau_{zx}}{\partial z}dz
\end{array}\right\}
\end{eqnarray*}
����āC$x$�������ψʂ�$u$�Ƃ��C���x��$\rho$�Ƃ���ƁC�����v�f�����̂�$x$�������̉^�������������̂悤�ɕ\�����邱�Ƃ��ł���D
\begin{eqnarray*}
\frac{d}{dt}\left(\rho dxdydz\frac{\partial u}{\partial t}\right) &=& \left\{\sigma_{xx}(x+dx,y,z,t) - \sigma_{xx}(x,y,z,t)\right\}dydz
+\left\{\tau_{xy}(x,y+dy,z,t) - \tau_{xy}(x,y,z,t)\right\}dzdx + \left\{\tau_{zx}(x,y,z+dz,t) - \tau_{zx}(x,y,z,t)\right\}dxdy \\
&=& \frac{\partial\sigma_{xx}}{\partial x}dxdydz + \frac{\partial\tau_{xy}}{\partial y}dydzdx + \frac{\partial\tau_{zx}}{\partial z}dzdxdy
\end{eqnarray*}
�����C���ӂ̑S�����͕Δ����Ɠ����Ȃ̂ŁC$x$�������̉^���������͎����ƂȂ�D
\begin{eqnarray*}
\rho\frac{\partial^2u}{\partial t^2} = \frac{\partial\sigma_{xx}}{\partial x} + \frac{\partial\tau_{xy}}{\partial y} + \frac{\partial\tau_{zx}}{\partial z}
\end{eqnarray*}
$y$���C$z$�������ɂ��Ă����l�ɍl���邱�Ƃ��ł���D
12.2 �_�̏c�U���ɑ���^��������
�@�_�̂ɂ����āC�������݂̂̕ό`��������ꍇ���l����D�ޗ������Ƃ��āC���x��$\rho$�C�c�e���W����$E$�Ƃ��C�`������Ƃ��ẮC�f�ʐς�$A$�ŁC������$l$�ł���Ƃ���D�}12-3�Ɏ����悤�ɁC�_��������$x$���W�����C���̈ʒu�̎������ψʂ�$u=u(x,t)$�Ƃ���D$x$�ʒu�����������$dx$�̕��������o���ƁC�}�Ɏ����悤�Ɏ������̈����艞��$\sigma_{xx}$���C���̕����ɍ�p���Ă���ƍl���邱�Ƃ��ł���D$x+dx$�̈ʒu�̉E���ɍ�p���鉞�͂ɂ���Taylor�W�J�����
\begin{eqnarray*}
\sigma_{xx}(x+dx,t) = \sigma_{xx}(x,t) + \frac{\partial\sigma_{xx}}{\partial x}dx + \frac{1}{2!}\frac{\partial^2\sigma_{xx}}{\partial x^2}dx^2 + \ldots
\end{eqnarray*}
�ƂȂ�̂ŁC$dx$�̂P�����݂̂��l�����邱�Ƃɂ��C��������$dx$�̕����̉^���������́CNewton�̑�Q�@����p���Ď��̂悤�ɕ\�����Ƃ��ł���D
\begin{eqnarray*}
\frac{d}{dt}\left(\rho Adx\frac{\partial u}{\partial t}\right) = \left\{\sigma_{xx}(x+dx,t)-\sigma_{xx}(x,t)\right\}A = \left(\frac{\partial\sigma_{xx}}{\partial x}dx \right)A
\end{eqnarray*}
\begin{eqnarray*}
\therefore \rho\frac{\partial^2u}{\partial t^2} = \frac{\partial\sigma_{xx}}{\partial x}
\end{eqnarray*}
���̂Ƃ��C$\sigma_{yy}=\sigma_{zz}=0$�ł���C�Ή�����$x$�������̐L�јc$\varepsilon_{xx}$�́C�������ޗ������肵�C�|�A�\�����$\nu$�Ƃ���ƁC
\begin{eqnarray*}
\varepsilon_{xx} = \frac{\sigma_{xx}}{E} - \frac{\nu}{E}\sigma_{yy} - \frac{\nu}{E}\sigma_{zz} = \frac{\sigma_{xx}}{E}
\end{eqnarray*}
�ƂȂ�̂ŁC������C�P���̉��͘c�W
\begin{eqnarray*}
\sigma_{xx}=E\varepsilon_{xx}
\end{eqnarray*}
����������D�����ŁC�������̐L�јc�́C���̂悤�ɒ�`�����D
\begin{eqnarray*}
\varepsilon_{xx} = \lim_{dx\rightarrow 0}\frac{u(x+dx,t)-u(x,t)}{dx} = \frac{\partial u(x,t)}{\partial x}=\frac{\partial u}{\partial x}
\end{eqnarray*}
�]���āC�^���������͎��̂悤�ɕό`�ł���D
\begin{eqnarray*}
\rho\frac{\partial^2u}{\partial t^2} = \frac{\partial}{\partial x}\left(E\varepsilon_{xx}\right)=\frac{\partial}{\partial x}\left(E\frac{\partial u}{\partial x}\right) = E\frac{\partial^2u}{\partial x^2}
\end{eqnarray*}
�����C�_�̂̎������Ɋւ���^���������͎����ƂȂ�D
\begin{eqnarray*}
&& \frac{\partial^2u}{\partial t^2} = c^2\frac{\partial^2u}{\partial x^2} \\
&& c=\sqrt{\frac{E}{\rho}}
\end{eqnarray*}
���̏ꍇ���ꎟ���̔g���������ƂȂ�D����āC�K���U�������肷�邱�Ƃɂ��C���E�����ɑ��āC�ŗL�p�U�����ƌŗL���[�h�����̏ꍇ�Ɠ��l�ɒ�߂邱�Ƃ��ł���D�܂��C���R�U�������Ɋւ��Ă����l�ɒ�߂邱�Ƃ��ł���i�͂��ł���j�D
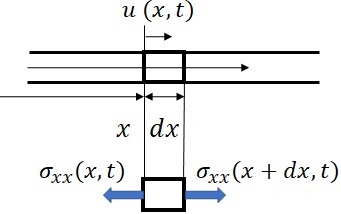
�}12-3�@�_�̂̎������U��
�@
12.3 Hamilton�̌�����p������b�������̓��o
��������$dx$�ɂ�����^���G�l���M�[$dT$�́C
\begin{eqnarray*}
dT =\frac{1}{2}\rho Adx\left(\frac{\partial u}{\partial t}\right)^2
\end{eqnarray*}
�_�S�̂ł͎����̂悤�ɂȂ�D
\begin{eqnarray*}
T =\int_0^l\frac{1}{2}\rho A\left(\frac{\partial u}{\partial t}\right)^2dx
\end{eqnarray*}
���l�ɁC�c�G�l���M�[�Ɋւ��āC��������$dx$�ɂ��čl�����
\begin{eqnarray*}
dU = \frac{1}{2}\sigma_{xx}A\varepsilon_{xx}dx = \frac{1}{2}EA\varepsilon_{xx}^2dx =\frac{1}{2}EA\left(\frac{\partial u}{\partial x}\right)^2dx
\end{eqnarray*}
����āC�_�S�̘̂c�G�l���M�[�͎����Ȃ�D
\begin{eqnarray*}
U = \int_0^l\frac{1}{2}EA\left(\frac{\partial u}{\partial x}\right)^2dx
\end{eqnarray*}
�X�ɁC��p��$Q(x,t)$�ɂ�鉼�z�d��$\delta W$���l����Ǝ����ƂȂ�D
\begin{eqnarray*}
\delta W =\int_0^lQ(x,t)\delta udx
\end{eqnarray*}
���̏ꍇ��Hamilton�̌����͎����ƂȂ�D
\begin{eqnarray*}
\int_t\delta\left(T-U\right)dt + \int_t\delta Wdt = 0
\end{eqnarray*}
��P���́C
\begin{eqnarray*}
\int_t\int_x\delta\left\{\frac{1}{2}\rho A\left(\frac{\partial u}{\partial t}\right)^2 - \frac{1}{2}EA\left(\frac{\partial u}{\partial x}\right)^2\right\}dxdt
\end{eqnarray*}
\begin{eqnarray*}
&& = \int_t\int_x\left[\rho A\frac{\partial u}{\partial t}\delta\left(\frac{\partial u}{\partial t}\right) - EA\frac{\partial u}{\partial x}\delta\left(\frac{\partial u}{\partial x}\right)\right]dxdt = \int_t\int_x\left[\rho A\frac{\partial u}{\partial t}\frac{\partial}{\partial t}\left(\delta u\right) - EA\frac{\partial u}{\partial x}\frac{\partial}{\partial x}\left(\delta u\right)\right]dxdt \\
&& = \int_x\left\{ \left[\rho A\frac{\partial u}{\partial t}\delta u\right]_t -\int_t\left\{\frac{\partial}{\partial t}\left(\rho A\frac{\partial u}{\partial t}\right)\delta u + EA\frac{\partial u}{\partial x}\frac{\partial}{\partial x}\left(\delta u\right)\right\}dt\right\}dx
\end{eqnarray*}
�^���̎n�߂ƏI���ŕψʂ��m�肷���$\delta u=0$�Ƃł���̂ŁC$t$�Ɋւ���ϕ��͗��������̂Ŏ��̗l�ɂȂ�D
\begin{eqnarray*}
&& = -\int_t\int_x\left[\frac{\partial}{\partial t}\left(\rho A\frac{\partial u}{\partial t}\right)\delta u + EA\frac{\partial u}{\partial x}\frac{\partial}{\partial x}\left(\delta u\right)\right]dxdt \\
&& = -\int_t\left\{\left[EA\frac{\partial u}{\partial x}\delta u\right]_x + \int_x\left\{\frac{\partial}{\partial t}\left(\rho A\frac{\partial u}{\partial t}\right) - \frac{\partial}{\partial x}\left(EA\frac{\partial u}{\partial x}\right)\right\}\delta udx\right\}dt
\end{eqnarray*}
��Q����������Ǝ����ƂȂ�D
\begin{eqnarray*}
\int_t\left\{-\left[EA\frac{\partial u}{\partial x}\delta u\right]_x + \int_x\left\{Q(x,t) - \rho A\frac{\partial^2u}{\partial t^2} + EA\frac{\partial^2u}{\partial x^2}\right\}\delta udx\right\}dt = 0
\end{eqnarray*}
����āC$\delta u$�͔C�ӂȂ̂ŁC�C�ӂ�$t$�C$x$�ɑ��āC���̊W���������邱�ƂɂȂ�D
\begin{eqnarray*}
Q(x,t) - \rho A\frac{\partial^2u}{\partial t^2} + EA\frac{\partial^2u}{\partial x^2} = 0
\end{eqnarray*}
�܂��C�C�ӂ̎����ɑ��Ď������������邱�Ƃ��K�v�ƂȂ�D
\begin{eqnarray*}
\left[EA\frac{\partial u}{\partial x}\delta u\right]_x = 0
\end{eqnarray*}
�ȏ�܂Ƃ߂�ƁCHamilton�̌������C�_�̏c�U���ɑ���^���������͎����ƂȂ�D
\begin{eqnarray*}
\rho\frac{\partial^2u}{\partial t^2} = E\frac{\partial^2u}{\partial x^2} + \frac{1}{A}Q(x,t)
\end{eqnarray*}
�܂��C���E���������̂悤�ɒ�܂�D
\begin{eqnarray*}
\left[EA\frac{\partial u}{\partial x}\delta u\right]_x = 0
\end{eqnarray*}
�����ŁC$E\frac{\partial u}{\partial x}=\sigma_{xx}$���C�����̂悤�ȕ\�����\�ł���D
\begin{eqnarray*}
\left[A\sigma_{xx}\delta u\right]_x = 0
\end{eqnarray*}
���[�ɍ�p����͂�$F_x$�Ƃ���ƁC$F_x=\sigma_{xx}A$���C���E�̗��[�ŗ͂��^������ꍇ�́C
\begin{eqnarray*}
\left[F_x\delta u\right]_x = 0
\end{eqnarray*}
�Ƃ������\�����ł���D
12.4 �ۖ_�̂˂���U��
�@���l�̈ꎟ���̔g���������̉^���������ƂȂ�C�ۖ_�̂˂���U���ɑ���^���������̓��o�ɂ��čl����D���̏ꍇ�C�}12-4�Ɏ����悤�Ɏ�������$x$���W�����C$x$�����̔C�ӓ_�̂˂���p��$\phi$�Ƃ��āC��������$dx$�̗��[�ɂ˂��胂�[�����g�l����D�˂���p��$x$���Ɋւ��ĉE�˂����i�ޕ����i���v���j�𐳂Ƃ��C���[�����g$M_x$�̕��������l�ɍl����D$x$���ɐ����Ȓf�ʏ��$\left(r,\theta\right)$���W�n���l���C�_�̖��x��$\rho$�Ƃ���ƁC��������$dx$�Ɋւ��鎲���̉�]�^���ɑ���^���������͎��̂悤�ɂȂ�D
\begin{eqnarray*}
\frac{\partial}{\partial t}\left(\int_r\int_\theta\rho r^2 drrd\theta dx \frac{\partial \phi}{\partial t}\right) = M_x(x+dx,t) - M_x(x,t)\fallingdotseq M(x,t) + \frac{\partial M_x}{\partial x}dx - M_x(x,t) = \frac{\partial M_x}{\partial x}dx
\end{eqnarray*}
\begin{eqnarray*}
\therefore \rho I_p\frac{\partial^2\phi}{\partial t^2} = \frac{\partial M_x}{\partial x}\text{, }\quad I_P = \int_r\int_\theta r^3 drd\theta
\end{eqnarray*}
����C$x$�����̂˂���p$\phi$�ɑ���$\left(r,\theta\right)$�f�ʂɔ������鉞��$\tau_{x\theta}$�́C���e���W����$G$�Ƃ���ƁC�Ή����陒�f�c$\gamma_{x\theta}$��p���Ď����ɂ悤�ɕ\���ł���D
\begin{eqnarray*}
\tau_{x\theta}=G\gamma_{x\theta}
\end{eqnarray*}
�f�ʓ��̉�]��$x$����$r$�̋����ɂ���ʒu��$\theta$�����ψʂ�$r\phi$�ł��邱�Ƃ���C���f�c$\gamma_{x\theta}$�͎��̂悤�ɕ\���ł���D
\begin{eqnarray*}
\gamma_{x\theta} = \lim_{dx\rightarrow 0}\frac{r\phi(x+dx,t)-r\phi(x,t)}{dx} = r\frac{\partial \phi}{\partial x}
\end{eqnarray*}
�f�ʂɓ����˂��胂�[�����g$M_x$�́C�˂��艞�͂ɘr�̒����ł���C��]������̋���$r$�������Ēf�ʏ�̐ϕ����s���悢�̂ŁC�����̂悤�ɕ\�����Ƃ��ł���D
\begin{eqnarray*}
M_x =\int_r\int_\theta r\times\tau_{x\theta}drrd\theta = \int_r\int_\theta r^2G\gamma_{x\theta}drd\theta = G\int_r\int_\theta r^3drd\theta \frac{\partial \phi}{\partial x}
\end{eqnarray*}
�����C�˂��胂�[�����g$M_x$�͎����ƂȂ�D
\begin{eqnarray*}
M_x = GI_P\frac{\partial \phi}{\partial x}
\end{eqnarray*}
����āC�˂���U���ɑΉ�����^���������͎��̂悤�ɂȂ�D
\begin{eqnarray*}
\rho I_p\frac{\partial^2\phi}{\partial t^2} = GI_P\frac{\partial^2\phi}{\partial x^2}
\end{eqnarray*}
\begin{eqnarray*}
\therefore \frac{\partial^2\phi}{\partial t^2} = c^2\frac{\partial^2\phi}{\partial x^2}\text{, }\quad c=\sqrt{\frac{G}{\rho}}
\end{eqnarray*}
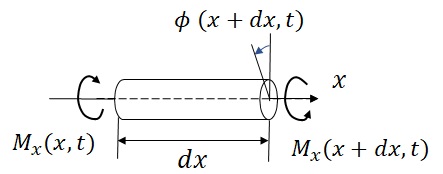
�}12-4�@�ۖ_�̂˂���U��
�@
12.5 ���K
����$l$�C���x$\rho$�C�c�e���W��$E$�̋ψ�f�ʖ_�����x$v$�ŕǖʂɏՓ˂���D�Ռ���C�Փ˖ʂ��ǖʂɌŒ�����Ƃ����ꍇ�̖_�̉��������߂�D
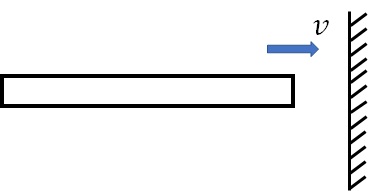
�}12-5�@�_�ƕǂ̏Փˌ�̂̎��R�U��
�@





