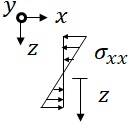13�D�A���̂̐U�����V�i���̋Ȃ��U���j
13.1 �����_�ɂ����鉼��
�@�@�B�V�X�e���̍\���̂Ɋ܂܂���v�ȗv�f����Ƃ��ĂƂ��Ď�舵���P�[�X�͐��������݂��C���x�̕ۏ�⓮�����c���Ȃǐv�i�K�ł̗L�p�����傫���D���Ƃ͈�ʂɕ��C���邢�́C���s�������̕ό`�͍l�����C��������ɐ����ȕ����̋Ȃ��ό`���l���郂�f���ł���C�Ȃ��ɂ���Đ�����f�ʓ��̐L�јc�ɂ�郂�[�����g���l���邱�Ƃɂ�肻�̌��ۂ𑨂��邱�ƂɂȂ�D
�@�}13-1�Ɏ����悤�ɗ��̒���������$x$���W�����C���̌��������̒����ʂɐ����ȕ�����$z$���W�����C$z=0$�ɂ����鉡�����i�Ȃ��j�ψʂ�$w=w(x,t)$�Ƃ��C�f�ʓ��̎������ψ�$U(x,z,t)$�C�y�сC�������ψ�$W(x,z,t)$���l����D�܂��C
1) �f�ʓ��̉������ψʂ͈��C���邢�́C�ǂ��������C�����C$W(x,z,t) = w(x,t)$�Ɖ��肷��D
2) ���̒����ʂ̎������̐L�т͗�C�����C$U(x.0,t)=0.0$
3) �f�ʂ͒����ʂɐ����Ȃ܂ܕό`����Ɖ��肷��D
�ȏォ��C�f�ʉ�]�p��$\theta$�Ƃ��āC�f�ʏ�̒����ʂ���$z$���ꂽ�ʒu�̎������ψʂ�����ό`�����肵��
\begin{eqnarray*}
U\left(x,z,t\right) = -z\sin\theta \fallingdotseq -z\theta
\end{eqnarray*}
�ŕ\�킷�D�X�ɁC
\begin{eqnarray*}
&& \tan\theta = \frac{\partial w(x,t)}{\partial x}\\
&& \therefore \theta \fallingdotseq \frac{\partial w(x,t)}{\partial x}
\end{eqnarray*}
���C�������ψʂ͎��̂悤�ɂȂ�D
\begin{eqnarray*}
U\left(x,z,t\right) = -z\frac{\partial w(x,t)}{\partial x}= -z\frac{\partial w}{\partial x}
\end{eqnarray*}
�����C����̔C�ӓ_$(x,z)$�̈ʒu�ɂ����鎲�����ψʂƉ������ψʂ́C���̒����ʂ̉������ψ�$w=w(x,t)$��p���āC�����ɂ悤�ɕ\�킳��邱�ƂɂȂ�D
\begin{eqnarray*}
\left.\begin{array}{l}
U\left(x,z,t\right) = U = -z\frac{\partial w}{\partial x} \\
W\left(x,z,t\right) = W = w
\end{array}\right\}
\end{eqnarray*}
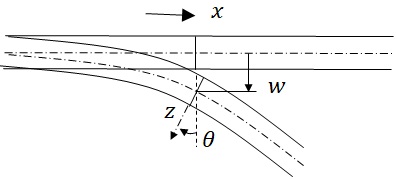
�}13-1�@�����f���ɂ����靚�ݕψ�$w$�ƒf�ʂ̗l�q
�@
13.2 ���̋Ȃ��U���ɑ���^��������
�P���̈�������$\sigma_{xx}$�ƑΉ�����L�јc$\varepsilon_{xx}$�ɂ����āC�ޗ��̏c�e���W����$E$�Ƃ���Ǝ����̂悤�ɂȂ�D
\begin{eqnarray*}
\sigma_{xx} = E\varepsilon_{xx} = E\frac{\partial U}{\partial x} = -Ez\frac{\partial^2w}{\partial x^2}
\end{eqnarray*}
�Ȃ��ό`�ɂ���Ēf�ʓ��ɔ�������������͂̃C���[�W�́C�}13-2�̂悤�ɂȂ�̂ŁC�����ʂ�$x$���W�_���̃��[�����g$M_x$��$x$�C$z$�ƉE��n�ƂȂ�$y$���W���X�ɉ����邱�Ƃɂ��C���̂悤�Ȏ��ŕ\���ł���D
\begin{eqnarray*}
M_x = \int_y\int_zz\sigma_{xx}dydz = -E\int_y\int_zz^2\frac{\partial^2w}{\partial x^2}dydz
\end{eqnarray*}
����āC
\begin{eqnarray*}
I = \int_y\int_zz^2dydz
\end{eqnarray*}
�ƒu���ƁC$x$�̒n�_�ɂ�����Ȃ����[�����g�͎����ŕ\���ł��邱�ƂɂȂ�D
\begin{eqnarray*}
M_x = -EI\frac{\partial^2w}{\partial x^2}
\end{eqnarray*}
$I$�͒f�ʓ��[�����g�ƌĂ�C$EI$�́C�Ȃ������ƌĂ�邱�Ƃ�����D
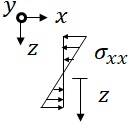
�}13-2�@��������$\sigma_{xx}$�̒f�ʏ�ł̕��z
�@
�^���������o���邽�߂ɁC��������$dx$�̗��[�ɍ�p���郂�[�����g$M_x$�ƙ��f��$Q_x$��}13-3�Ɏ����D$M_x=M_x(x,t)$�C$Q_x=Q_x(x,t)$�ł���̂ŁC$x+dx$�̈ʒu�ƂȂ�E���̃��[�����g�C�y�љ��f�͎͂��̂悤�ɂȂ�D
\begin{eqnarray*}
&& M_x(x+dx,t) = M_x(x,t) + \frac{\partial M_x(x,t)}{\partial x}dx + \frac{1}{2!}\frac{\partial^2M_x(x,t)}{\partial x^2}dx^2 + \ldots \fallingdotseq M_x(x,t) + \frac{\partial M_x(x,t)}{\partial x}dx\\
&& Q_x(x+dx,t) = Q_x(x,t) + \frac{\partial Q_x(x,t)}{\partial x}dx + \frac{1}{2!|}\frac{\partial^2Q_x(x,t)}{\partial x^2}dx^2 + \ldots \fallingdotseq Q_x(x,t) + \frac{\partial Q_x(x,t)}{\partial x}dx\\
\end{eqnarray*}
���̖��x��$\rho$�C�f�ʐς�$A$�Ƃ���ƁCNewton�̑��@�����C������D
\begin{eqnarray*}
\frac{\partial }{\partial t}\left(\rho Adx\frac{\partial w}{\partial t}\right) = Q_x(x+dx,t) - Q_x(x,t) = \frac{\partial Q_x}{\partial x}dx
\end{eqnarray*}
����Ď����ƂȂ�D
\begin{eqnarray*}
\rho A\frac{\partial^2w}{\partial t^2} = \frac{\partial Q_x}{\partial x}
\end{eqnarray*}
��]�����͏������Ƃ��āC$x+dX$�����x�_�Ƃ��郂�[�����g�̒ލ������l�����
\begin{eqnarray*}
M_x(x+dx,t) - \left\{M_x(x,t) + Q_x(x,t)dx\right\} = 0
\end{eqnarray*}
\begin{eqnarray*}
\therefore \frac{\partial M_x(x,t)}{\partial x}dx - Q_x(x,t)dx = 0
\end{eqnarray*}
�����C
\begin{eqnarray*}
Q_x = \frac{\partial M_x}{\partial x}
\end{eqnarray*}
�̊W����܂�̂ŁC�^���������͎��̂悤�ɂȂ�D
\begin{eqnarray*}
\rho A\frac{\partial^2w}{\partial t^2} = \frac{\partial^2M_x}{\partial x^2} = -\frac{\partial^2}{\partial x^2}\left(EI\frac{\partial^2w}{\partial x^2}\right)
\end{eqnarray*}
�����ŁC$EI$��$x$�ɑ��Ĉ��Ȃ�C���̂悤�Ȍ`�̉^�����������߂邱�Ƃ��ł���D
\begin{eqnarray*}
\rho A\frac{\partial^2w}{\partial t^2} + EI\frac{\partial^4w}{\partial x^4} = 0
\end{eqnarray*}
����́CEuler-Berronoulii���ƌĂ������f���̉^���������ŁC�莮���ł��������肩��C�h���f�ό`�h�Ɓh��]�����h���������f���ƌ�����D
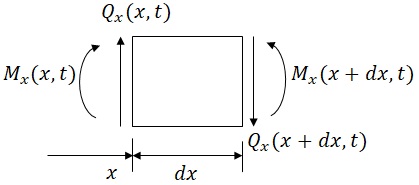
�}13-3�@�����v�f$dx$�����ɍ�p���郂�[�����g�ƙ��f��
�@
13.3 Hamilton�̌�����p������b�������̓��o
���̒�����$l$�Ƃ���ƁC���S�̂̉^���G�l���M�[$T$�͎����ŕ\�����Ƃ��ł���D
\begin{eqnarray*}
T=\int_z\int_y\int_0^l\frac{1}{2}\rho\left(\frac{\partial w}{\partial t}\right)^2dxdydx = \frac{1}{2}\rho A\int_0^l\left(\frac{\partial w}{\partial t}\right)^2dx
\end{eqnarray*}
�����ŁC
\begin{eqnarray*}
A=\int_z\int_ydydx
\end{eqnarray*}
�͒f�ʐςł���D����C�c�G�l���M�[$U$�́C
\begin{eqnarray*}
U=\int_z\int_y\int_0^l\frac{1}{2}\sigma_{xx}\varepsilon_{xx}dxdydx = \int_z\int_y\int_0^l\frac{1}{2}Ez^2\left(\frac{\partial^2w}{\partial x^2}\right)^2dxdydz = \frac{1}{2}EI\int_0^l\left(\frac{\partial^2w}{\partial x^2}\right)^2dx
\end{eqnarray*}
Hamilton�̌����͎����ŕ\�������D
\begin{eqnarray*}
\int_t\delta\left(T-U\right)dt = 0
\end{eqnarray*}
\begin{eqnarray*}
\therefore \int_t\delta\left\{ \frac{1}{2}\rho A\int_0^l\left(\frac{\partial w}{\partial t}\right)^2dx-\frac{1}{2}EI\int_0^l\left(\frac{\partial^2w}{\partial x^2}\right)^2dx\right\}dt = 0
\end{eqnarray*}
����āC
\begin{eqnarray*}
\int_t\int_0^l\left[ \rho A\frac{\partial w}{\partial t}\delta\left(\frac{\partial w}{\partial t}\right)-EI\frac{\partial^2w}{\partial x^2}\delta\left(\frac{\partial^2w}{\partial x^2}\right)\right]dxdt = 0
\end{eqnarray*}
$\delta$�ƕΔ��������ւ����
\begin{eqnarray*}
\int_t\int_0^l\left[ \rho A\frac{\partial w}{\partial t}\frac{\partial}{\partial t}\left(\delta w\right)-EI\frac{\partial^2w}{\partial x^2}\frac{\partial^2}{\partial x^2}\left(\delta w\right)\right]dxdt = 0
\end{eqnarray*}
$t$�ɂ��ĕ����ϕ�����ƁC
\begin{eqnarray*}
\int_x\left[\rho A\frac{\partial w}{\partial t}\delta w\right]_tdx - \int_t\int_0^l\left[\frac{\partial}{\partial t}\left(\rho A\frac{\partial w}{\partial t}\right)\delta w + EI\frac{\partial^2w}{\partial x^2}\frac{\partial^2}{\partial x^2}\left(\delta w\right)\right]dxdt = 0
\end{eqnarray*}
�^���̊J�n�ƏI����$w$����܂�Ƃ����$\left[\delta w\right]_t=0$�ƂȂ�̂ŁC��ꍀ�͗�ƂȂ�̂ŁC�c��̍��Ɋւ��āC$x$�ŕ����ϕ�����Ǝ�����D
\begin{eqnarray*}
\int_t\left\{\left[EI\frac{\partial^2w}{\partial x^2}\frac{\partial}{\partial x}\left(\delta w\right)\right]_0^l + \int_0^l\left[\frac{\partial}{\partial t}\left(\rho A\frac{\partial w}{\partial t}\right)\delta w - \frac{\partial}{\partial x}\left(EI\frac{\partial^2w}{\partial x^2}\right)\frac{\partial}{\partial x}\left(\delta w\right)\right]dx\right\} dt = 0
\end{eqnarray*}
�X�ɂ������C$x$�ŕ����ϕ�����Ǝ����ƂȂ�D
\begin{eqnarray*}
\int_t\left\{\left[EI\frac{\partial^2w}{\partial x^2}\delta\left(\frac{\partial w}{\partial x}\right)\right]_0^l - \left[\frac{\partial}{\partial x}\left(EI\frac{\partial^2w}{\partial x^2}\right)\delta w\right]_0^l + \int_0^l\left[\frac{\partial}{\partial t}\left(\rho A\frac{\partial w}{\partial t}\right) + \frac{\partial^2}{\partial x^2}\left(EI\frac{\partial^2w}{\partial x^2}\right)\right]\delta wdx\right\} dt = 0
\end{eqnarray*}
����āC$\delta w$�͔C�ӂł���̂ŁCHamilton�̌��������藧���߂ɂ́C�܂��C�C�ӂ̎���$t$�C�C�ӂ̈ʒu$x$�ɑ��āC$\delta w$�Ŋ����Ă���
\begin{eqnarray*}
\frac{\partial}{\partial t}\left(\rho A\frac{\partial w}{\partial t}\right) + \frac{\partial^2}{\partial x^2}\left(EI\frac{\partial^2w}{\partial x^2}\right) = 0
\end{eqnarray*}
���������C���C�C�ӂ̎���$t$�ɑ��āC
\begin{eqnarray*}
\left[EI\frac{\partial^2w}{\partial x^2}\delta\left(\frac{\partial w}{\partial x}\right)\right]_0^l = 0 \text{, }\quad\left[\frac{\partial}{\partial x}\left(EI\frac{\partial^2w}{\partial x^2}\right)\delta w\right]_0^l = 0
\end{eqnarray*}
����������K�v������D�O�҂́C���̉^���������ł���C��҂͗��̉^�����߂�̂ɕK�v�ƂȂ鋫�E�����ł���D
13.4 �ŗL�U�����ƌŗL���[�h
�@���̋Ȃ��U���Ɋւ��āC�K���U�����l�����
\begin{eqnarray*}
w=w(x,t) = W_n(x) e^{i\omega_n t}
\end{eqnarray*}
�ƒu�����Ƃ��ł���̂ŁC���̊e�p�����[�^$EI$�C$\rho A$�Ȃǂ̂��������Ɉ��̎��ɂ́C�����̂悤�ɂȂ�D
\begin{eqnarray*}
-\rho A\omega_n^2W_n(x) + EI\frac{d^4W_n(x)}{dx^4} = 0
\end{eqnarray*}
\begin{eqnarray*}
\therefore \frac{d^4W_n(x)}{dx^4} - \frac{\rho A\omega_n^2}{EI}W_n(x) = 0
\end{eqnarray*}
����āC$W_n(x)= Y_n e^{\lambda x}$�Ƃ����ƁC������������
\begin{eqnarray*}
\lambda^4 = \frac{\rho A\omega_n^2}{EI}
\end{eqnarray*}
�ƂȂ�̂ŁC���̂悤�ȂS�̓���������܂�D
\begin{eqnarray*}
\lambda = \pm\sqrt[4]{\frac{\rho A\omega_n^2}{EI}}\text{, }\quad\pm i\sqrt[4]{\frac{\rho A\omega_n^2}{EI}}
\end{eqnarray*}
����āC$\beta_n=\sqrt[4]{\frac{\rho A\omega_n^2}{EI}}$�ƒu���ƁC$W_n(x)$�̈�ʉ��͎����̂悤�ɏ������Ƃ��ł���D
\begin{eqnarray*}
W_n(x) = c_1e^{\beta_n x}+c_2e^{-\beta_n x}+c_3e^{i\beta_n x}+c_4e^{-i\beta_n x}
\end{eqnarray*}
�����ŁC���̂悤�ȕό`������D
\begin{eqnarray*}
W_n(x) &=& \left(c_1+c_2\right)\frac{e^{\beta_n x}+e^{-\beta_n x}}{2} + \left(c_1-c_2\right)\frac{e^{\beta_n x}-e^{-\beta_n x}}{2} + \left(c_3+c_4\right)\frac{e^{i\beta_n x}+e^{-i\beta_n x}}{2} + \left(c_3-c_4\right)\frac{e^{i\beta_n x}-e^{-i\beta_n x}}{2} \\
&=& a_1\cosh\beta_nx + b_1\sinh\beta_nx + a_2\cos\beta_nx + b_2\sin\beta_nx
\end{eqnarray*}
���ꂪ�C�����f���ɂ��������[�h���ł���C���E������^���邱�Ƃɂ��C���̌ŗL���[�h���̕��z�`��ƌŗL�U�������߂邱�Ƃ��ł���D
��F���[�P���x��
�����ŁC���̗��[�C�����C$x=0$�C$x=l$�ɂ����āC���ɁC$w=0$�C$M_x=0$�ƂȂ鋫�E�������l���Ă݂�D���E�������l����ꍇ�́C$W_n(x)$�ɑ��ď�����ݒ肷��悢�̂ŁC���̏ꍇ�C���̂S�W����܂�D
\begin{eqnarray*}
\left.\begin{array}{l}
W(0) = 0 \\
\frac{d^2W(0)}{dx^2} = 0 \\
W(l) = 0 \\
\frac{d^2W(l)}{dx^2} = 0
\end{array}\right\}
\end{eqnarray*}
����āC����[�h����莟���ƂȂ�D
\begin{eqnarray*}
\left.\begin{array}{l}
W(0) = a_1 + a_2 = 0 \\
\frac{d^2W(0)}{dx^2} = \beta^2\left(a_1 - a_2\right) = 0 \\
W(l) = a_1\cosh\beta_nl + b_1\sinh\beta_nl + a_2\cos\beta_nl + b_2\sin\beta_nl =0 \\
\frac{d^2W(l)}{dx^2} = \beta_n^2\left(a_1\cosh\beta_nl + b_1\sinh\beta_nl - a_2\cos\beta_nl - b_2\sin\beta_nl\right) = 0
\end{array}\right\}
\end{eqnarray*}
����āC���̂Q���ƂȂ�D
\begin{eqnarray*}
\left.\begin{array}{l}
b_1\sinh\beta_nl + b_2\sin\beta_nl =0 \\
b_1\sinh\beta_nl - b_2\sin\beta_nl = 0
\end{array}\right\}
\end{eqnarray*}
����āC$b_1$�C$b_2$�����ɗ�Ƃ͂Ȃ�Ȃ��������l�����
\begin{eqnarray*}
\sinh\beta_nl\sin\beta_nl =0
\end{eqnarray*}
�ƂȂ�C$\sinh\beta_nl =0$�́C$\beta_nl=0$�̂Ƃ��݂̂Ȃ̂ŁC���̏ꍇ�̐U�����������͎����ƂȂ�D
\begin{eqnarray*}
\sin\beta_nl =0
\end{eqnarray*}
�܂��C$b_1=0$�Ƃ����ėǂ��̂ŁC����W����$b_2$�݂̂ƂȂ�D����āC
\begin{eqnarray*}
\beta_nl =n \pi \quad \left(n=1,2,\ldots,\right)
\end{eqnarray*}
�ƂȂ�̂ŁC
\begin{eqnarray*}
\beta_n=\sqrt[4]{\frac{\rho A\omega_n^2}{EI}} = \frac{n\pi}{l}
\end{eqnarray*}
���C�ŗL�p�U����$\omega_n$�͎��̂悤�ɂȂ�D
\begin{eqnarray*}
&& \frac{\rho A\omega_n^2}{EI} = \left(\frac{n\pi}{l}\right)^4 \\
&& \omega_n^2 = \left(\frac{n\pi}{l}\right)^4\frac{EI}{\rho A} \\
&& \therefore \omega_n = \left(\frac{n\pi}{l}\right)^2\sqrt{\frac{EI}{\rho A}}
\end{eqnarray*}
���̂Ƃ��C����[�h����
\begin{eqnarray*}
W_n(x) = \sin\beta_nx = \sin\frac{n\pi x}{l}
\end{eqnarray*}
�ƂȂ�D
13.5 ���K
(1) ���[�P���x�����Ɋւ��āC�����ɗ��̎��ʂ����ׂďW�����Ă���Ƃ��Ē�܂�u�������ʁv�Ɨ������ɏW���d����p���Ă���Ɖ��肵�Ē�܂�u�����˒萔�v����Ȃ�1���R�x�U���n�̌ŗL�p�U�����ƁC�����_�ɂ���܂錋�ʂ��r���C�덷���v�Z����D