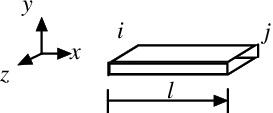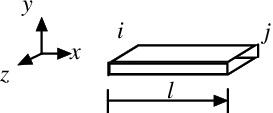3.弾性力学における有限要素定式化
3.1 1次元問題
3.1.1 重み付残差法に基づく定式化
棒や梁の縦振動問題である1次元応力問題に対して有限要素法を適用し,基礎方程式を誘導する.単軸圧縮・引張に対する基礎方程式は,軸方向変位を$u$とすると,
\begin{eqnarray*}
\frac{\partial\sigma_{xx}}{\partial x} - \rho\frac{\partial^2u}{\partial t^2} =0
\end{eqnarray*}
であり,仮想変位$\delta u$を重み関数とする重み付残差表現は次のように表わすことができる.
\begin{equation}
\int_x\int_y\int_z\left(\frac{\partial\sigma_{xx}}{\partial x} - \rho\frac{\partial^2u}{\partial t^2}\right)\delta udxdydz=0 \label{eqn:332}
\end{equation}
さらに,$x=x_k$($k=0$, $1$, $2$, $\ldots$)の位置に集中荷重$f_k\left(t\right)$が作用する場合には,Diracのデルタ関数$\delta\left(x\right)$を用いて,次のように表現することができる.
\begin{equation}
\int_x\int_y\int_z\left\{\frac{\partial \sigma_{xx}}{\partial x} - \rho\frac{\partial^2 u}{\partial t^2} + \sum_kf_k\left(t\right)\delta\left(x-x_k\right)\delta\left(y\right)\delta\left(z\right)\right\}\delta udxdydz=0 \label{eqn:333}
\end{equation}
この式の左辺第1項を部分積分し,次のように変形する.
\begin{eqnarray*}
\int_y\int_z\left[\sigma_{xx}\delta u\right]_xdydz -\int_x\int_y\int_z\sigma_{xx}\frac{\partial\delta u}{\partial x}dxdydz - \int_x\int_y\int_z\rho\frac{\partial^2 u}{\partial t^2}\delta udxdydz = \int_x\sum_kf_k\left(t\right)\delta\left(x-x_k\right)\delta u dx
\end{eqnarray*}
境界条件が厳密に満足されているとすると,第1項は零となる.応力,変位がベクトルで表現される場合には,その積は内積となるので次式のように$\delta u$の転置を左から掛ける形式で表わすことができる.
\begin{equation}
\int_x\int_y\int_z\left(\frac{\partial\delta u}{\partial x}\right)^T\sigma_{xx}dxdydz + \int_x\int_y\int_z\delta u^T\rho\frac{\partial^2u}{\partial t^2}dxdydz= \int_x\delta u^T\sum_kf_k\left(t\right)\delta\left(x-x_k\right)dx \label{eqn:333a}
\end{equation}
ここで,応力‐歪み関係は
\begin{eqnarray*}
\sigma_{xx} = E\varepsilon_{xx}
\end{eqnarray*}
であり,歪‐変位の関係は
\begin{eqnarray*}
\varepsilon_{xx} = \frac{\partial u}{\partial x}
\end{eqnarray*}
である.
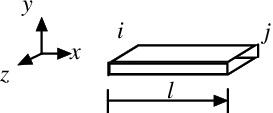
図 3.1 Finite element of a bar
図3.1に示すように,解析対象である棒,あるいは,梁の一部の有限な要素を取り出す.要素長さを$l$とし,要素両端を節点として,節点番号$i$番,$j$番を付ける.各節点における軸方向変位を$u_i$,$u_j$とし,局所座標系$xyz$を考える.各節点においては,作用反作用の法則により内力が発生しており,$i$点では,$-x$軸方向の力$f_i$,$j$点では,$x$軸方向の力$f_j$がこの要素に対して作用し,その反力が隣り合う別の要素に作用している,と考える.次に,要素内の$x$軸上の任意点の変位$u$を適当な関数で補間(近似)する.例えば,一次関数を仮定すると次のように表現できる.
\begin{equation}
u = u\left(x, t\right) = \left(1-\frac{x}{l}\right)u_i\left(t\right) + \frac{x}{l}u_j\left(t\right)
= \left\{\begin{array}{cc} 1-\frac{x}{l} & \frac{x}{l}\end{array}\right\}\left\{\begin{array}{c} u_i\left(t\right) \\ u_j\left(t\right) \end{array}\right\}
= \mathbf{N}\left(x\right)\left\{\begin{array}{c} u_i\left(t\right) \\ u_j\left(t\right) \end{array}\right\} \label{eqn:3001}
\end{equation}
ここで,$\mathbf{N}\left(x\right)$は,形状関数と呼ばれる.この第1変分,あるいは,仮想仕事$\delta u$は,
\begin{equation}
\delta u = \left(1-\frac{x}{l}\right)\delta u_i + \frac{x}{l}\delta u_j
= \left\{\begin{array}{cc} 1-\frac{x}{l} & \frac{x}{l}\end{array}\right\}\left\{\begin{array}{c} \delta u_i \\ \delta u_j \end{array}\right\}
= N\left(x\right)\left\{\begin{array}{c} u_i\left(t\right) \\ u_j\left(t\right) \end{array}\right\} \label{eqn:3002}
\end{equation}
と表現できる.また,歪に関して,$L=\frac{\partial}{\partial x}$として,
\begin{eqnarray*}
\varepsilon_{xx} = Lu = \frac{\partial u}{\partial x} = \left\{\begin{array}{cc} -\frac{1}{l} & \frac{1}{l}\end{array}\right\}
\left\{\begin{array}{c} u_i\left(t\right) \\ u_j\left(t\right) \end{array}\right\}= \mathbf{B}\left\{\begin{array}{c} u_i\left(t\right) \\ u_j\left(t\right) \end{array}\right\}
\end{eqnarray*}
同様に,変位成分の第1変分は,
\begin{eqnarray*}
\frac{\partial\delta u}{\partial x} = \left\{\begin{array}{cc} -\frac{1}{l} & \frac{1}{l}\end{array}\right\}
\left\{\begin{array}{c} \delta u_i \\ \delta u_j \end{array}\right\}=\mathbf{B}\left\{\begin{array}{c} \delta u_i \\ \delta u_j \end{array}\right\}
\end{eqnarray*}
よって,式(\ref{eqn:333a})右辺第1項は次のようになる.
\begin{eqnarray*}
\int_x\int_y\int_z\left(\frac{\partial\delta u}{\partial x}\right)^T\sigma_{xx}dxdydz &=& \int_x\int_y\int_z\left(\frac{\partial\delta u}{\partial x}\right)^TE\frac{\partial u}{\partial x}dxdydz \\
&=&\left\{\begin{array}{cc} \delta u_i & \delta u_j \end{array}\right\}\int_0^l\mathbf{B}^TEA\mathbf{B}dx\left\{\begin{array}{c} u_i \\ u_j \end{array}\right\} \\
&=& \left\{\begin{array}{cc} \delta u_i & \delta u_j \end{array}\right\}\int_0^lEA
\left\{\begin{array}{c} -\frac{1}{l} \\ \frac{1}{l}\end{array}\right\}
\left\{\begin{array}{cc} -\frac{1}{l} & \frac{1}{l}\end{array}\right\}dx
\left\{\begin{array}{c} u_i \\ u_j \end{array}\right\} \\
&=&\left\{\begin{array}{cc} \delta u_i & \delta u_j \end{array}\right\}\int_0^lEA
\left[\begin{array}{cc} \frac{1}{l^2} & -\frac{1}{l^2} \\
-\frac{1}{l^2} & \frac{1}{l^2}\end{array} \right]dx
\left\{\begin{array}{c} u_i\left(t\right) \\ u_j\left(t\right) \end{array}\right\} \\
&=&\left\{\begin{array}{cc} \delta u_i & \delta u_j \end{array}\right\}
\left[\begin{array}{cc} \frac{EA}{l} & -\frac{EA}{l} \\
-\frac{EA}{l} & \frac{EA}{l}\end{array} \right]
\left\{\begin{array}{c} u_i\left(t\right) \\ u_j\left(t\right) \end{array}\right\}
=\left\{\begin{array}{cc} \delta u_i & \delta u_j \end{array}\right\}
\mathbf{K}_{ij}\left\{\begin{array}{c} u_i\left(t\right) \\ u_j\left(t\right) \end{array}\right\}
\end{eqnarray*}
ここで,要素内において$EA$は一定としており,$D=EA$とおくと,
\begin{eqnarray*}
\mathbf{K}_{ij}=\int_0^l\mathbf{B}^TD\mathbf{B}dx = \left[\begin{array}{cc} \frac{EA}{l} & -\frac{EA}{l} \\
-\frac{EA}{l} & \frac{EA}{l}\end{array} \right]\text{, }A= \int_y\int_z dydz
\end{eqnarray*}
は,それぞれ,要素剛性行列,断面積である.一方,加速度は次のようになる.
\begin{eqnarray*}
\frac{\partial^2u}{\partial t^2} = \left\{\begin{array}{cc} 1-\frac{x}{l} & \frac{x}{l}\end{array}\right\}\left\{\begin{array}{c} \frac{d^2 u_i\left(t\right)}{dt^2} \\ \frac{du_j\left(t\right)}{dt^2} \end{array}\right\} = N\left(x\right)\left\{\begin{array}{c} \frac{du_i\left(t\right)}{dt^2} \\ \frac{d^2 u_j\left(t\right)}{dt^2} \end{array}\right\}
\end{eqnarray*}
よって,式(\ref{eqn:333a})右辺第2項は次のようになる.
\begin{eqnarray*}
\int_x\int_y\int_z\delta u^T\rho\frac{\partial^2u}{\partial t^2}dxdydz &=& \left\{\begin{array}{cc} \delta u_i & \delta u_j \end{array}\right\}\int_0^l\mathbf{N}\left(x\right)^T\rho A\mathbf{N}\left(x\right)dx\left\{\begin{array}{c} \frac{d^2u_i\left(t\right)}{dt^2} \\ \frac{d^2u_j\left(t\right)}{dt^2} \end{array}\right\} \\
&=& \left\{\begin{array}{cc} \delta u_i & \delta u_j \end{array}\right\}\int_0^l\left\{\begin{array}{c} 1-\frac{x}{l} \\ \frac{x}{l}\end{array}\right\}\rho A\left\{\begin{array}{cc} 1-\frac{x}{l} & \frac{x}{l}\end{array}\right\}dx\left\{\begin{array}{c} \frac{d^2u_i\left(t\right)}{dt^2} \\ \frac{d^2u_j\left(t\right)}{dt^2} \end{array}\right\} \\
&=& \left\{\begin{array}{cc} \delta u_i & \delta u_j \end{array}\right\}\int_0^l\rho A\left[\begin{array}{cc} \left(1-\frac{x}{l}\right)^2 & \frac{x}{l}\left(1-\frac{x}{l}\right)\\
\frac{x}{l}\left(1-\frac{x}{l}\right) & \left(\frac{x}{l}\right)^2 \end{array}\right]dx
\left\{\begin{array}{c} \frac{d^2u_i\left(t\right)}{dt^2} \\ \frac{du_j\left(t\right)}{dt^2} \end{array}\right\}\\
&=& \left\{\begin{array}{cc} \delta u_i & \delta u_j \end{array}\right\}\rho A\left[\begin{array}{cc} \frac{l}{3} & \frac{l}{6} \\
\frac{l}{6} & \frac{l}{3} \end{array}\right]
\left\{\begin{array}{c} \frac{d^2u_i\left(t\right)}{dt^2} \\ \frac{d^2u_j\left(t\right)}{dt^2} \end{array}\right\} = \left\{\begin{array}{cc} \delta u_i & \delta u_j \end{array}\right\}\mathbf{M}_{ij}\left\{\begin{array}{c} \frac{d^2u_i\left(t\right)}{dt^2} \\ \frac{d^2u_j\left(t\right)}{dt^2} \end{array}\right\}
\end{eqnarray*}
ここで,要素内において$\rho A$は一定としており,
\begin{eqnarray*}
\mathbf{M}_{ij}=\left[\begin{array}{cc} \frac{\rho Al}{3} & \frac{\rho Al}{6} \\
\frac{\rho Al}{6} & \frac{\rho Al}{3} \end{array}\right]
\end{eqnarray*}
は要素質量行列である.このように,形状関数$\mathbf{N}\left(x\right)$を用いて,求められた質量行列をconsistent mass matrixと呼び場合がある.これに対して,Lamped mass matrixと呼ぶ,対角成分のみ値を持つ質量行列を用いて解析を行う場合もある.各要素の和が,有限要素の質量$\rho Al$となるので,この場合のLamped mass matrixは,
\begin{eqnarray*}
\mathbf{M}_{ij}=\left[\begin{array}{cc} \frac{\rho Al}{2} & 0 \\
0 & \frac{\rho Al}{2} \end{array}\right]
\end{eqnarray*}
となる.
内力を考慮した次のような方程式を求めることができる.
\begin{eqnarray*}
\left\{\begin{array}{cc} \delta u_i & \delta u_j \end{array}\right\}\left(\mathbf{K}_{ij}\left\{\begin{array}{c} u_i\left(t\right) \\ u_j\left(t\right) \end{array}\right\}
+ \mathbf{M}_{ij}\left\{\begin{array}{c} \frac{d^2u_i\left(t\right)}{dt^2} \\ \frac{d^2u_j\left(t\right)}{dt^2} \end{array}\right\}
- \left\{\begin{array}{c} -f_i\left(t\right) \\ f_j\left(t\right) \end{array}\right\}
\right)=0
\end{eqnarray*}
したがって,各有限な要素に対して,次の関係が成立していることになる.
\begin{eqnarray}
\mathbf{M}_{ij}\left\{\begin{array}{c} \frac{d^2u_i\left(t\right)}{dt^2} \\ \frac{d^2u_j\left(t\right)}{dt^2} \end{array}\right\}+ \mathbf{K}_{ij}\left\{\begin{array}{c} u_i\left(t\right) \\ u_j\left(t\right) \end{array}\right\} = \left\{\begin{array}{c} -f_i\left(t\right) \\ f_j\left(t\right) \end{array}\right\} \label{eqn:334}
\end{eqnarray}
この要素とつながっている両端の要素に関しても同様の関係が成立しており,節点番号$i$番側に対しては,
\begin{eqnarray}
\mathbf{M}_{li}\left\{\begin{array}{c} \frac{d^2u_l\left(t\right)}{dt^2} \\ \frac{d^2u_i\left(t\right)}{dt^2} \end{array}\right\}+ \mathbf{K}_{li}\left\{\begin{array}{c} u_l\left(t\right) \\ u_i\left(t\right) \end{array}\right\} = \left\{\begin{array}{c} -f_l\left(t\right) \\ f_i\left(t\right) \end{array}\right\} \label{eqn:335}
\end{eqnarray}
また,節点番号$j$番側に対しては,
\begin{eqnarray}
\mathbf{M}_{jk}\left\{\begin{array}{c} \frac{d^2u_j\left(t\right)}{dt^2} \\ \frac{d^2u_k\left(t\right)}{dt^2} \end{array}\right\}+ \mathbf{K}_{jk}\left\{\begin{array}{c} u_j\left(t\right) \\ u_k\left(t\right) \end{array}\right\} = \left\{\begin{array}{c} -f_j\left(t\right) \\ f_k\left(t\right) \end{array}\right\} \label{eqn:336}
\end{eqnarray}
である.よって,要素全体で考えている節点番号に対応した節点変位$u_i$を要素とする節点変位ベクトル$\mathbf{u}\left(t\right)$を作り,それに対応する形で内力が打ち消しあうように,これらの方程式を加算することにより,次のような棒,あるいは,梁全体に関する基礎方程式を求めることができる.
\begin{eqnarray*}
\mathbf{M}\frac{d^2\mathbf{u}\left(t\right)}{dt^2} + \mathbf{K}\mathbf{u}\left(t\right) = \mathbf{f}_{0N}\left(t\right)
\end{eqnarray*}
ここで,
\begin{eqnarray*}
\mathbf{f}_{0N}\left(t\right)=\left\{\begin{array}{cccc} -f_0\left(t\right), & 0 &, \ldots, & f_N\left(t\right) \end{array}\right\}^T
\end{eqnarray*}
であり,両端が拘束されていない場合は,反力が発生しないので零ベクトルとなる.拘束を受けている場合は,それに対応した反力が発生していることになり,値は,境界の拘束状態によって定められる.変位ベクトル$\mathbf{u}\left(t\right)$は,要素数をNとすると,節点数はN+1個となり次のような形式となる.
\begin{eqnarray*}
\mathbf{u}\left(t\right)=\left\{\begin{array}{cccc} u_0\left(t\right), & u_1\left(t\right) & \ldots, & u_N\left(t\right)\end{array}\right\}^T
\end{eqnarray*}
各節点に加わる外力ベクトル$\mathbf{f}\left(t\right)$が存在する場合は,両端を含め次の形式で表現する.
\begin{eqnarray*}
\mathbf{f}\left(t\right)=\left\{\begin{array}{cccc} f_0\left(t\right), & f_1\left(t\right) & \ldots, & f_N\left(t\right)\end{array}\right\}^T
\end{eqnarray*}
即ち,各成分を対応する節点に加わる力と見なすことにより,次式が得られる.
\begin{eqnarray*}
\mathbf{M}\frac{d^2\mathbf{u}\left(t\right)}{dt^2} + \mathbf{K}\mathbf{u}\left(t\right) = \mathbf{f}\left(t\right)
\end{eqnarray*}
以上の導出方法は,式(\ref{eqn:332}),あるいは,式(\ref{eqn:333})において,領域内の支配(微分)方程式を
\begin{eqnarray*}
&& \frac{\partial\sigma_{xx}}{\partial x} - \rho\frac{\partial^2u}{\partial t^2} =0 \\
&& \frac{\partial\sigma_{xx}}{\partial x} - \rho\frac{\partial^2u}{\partial t^2} + \sum_kf_k\left(t\right)\delta\left(x-x_k\right)\delta\left(y\right)\delta\left(z\right) = 0
\end{eqnarray*}
関数で近似したために生じる誤差(残差)
\begin{eqnarray*}
&& \epsilon_1 = \frac{\partial\sigma_{xx}}{\partial x} - \rho\frac{\partial^2u}{\partial t^2} \\
&& \epsilon_2 = \frac{\partial\sigma_{xx}}{\partial x} - \rho\frac{\partial^2u}{\partial t^2} + \sum_kf_k\left(t\right)\delta\left(x-x_k\right)\delta\left(y\right)\delta\left(z\right)
\end{eqnarray*}
を零にするような関係式を,重み関数$\delta u=w$をかけ,領域$\Omega$に関する積分
\begin{eqnarray*}
&& \int_{\Omega}\epsilon_1 w d\Omega = 0 \\
&& \int_{\Omega}\epsilon_2 w d\Omega = 0
\end{eqnarray*}
を実行することにより求める,という考え方である.
3.1.2 エネルギー原理に基づく定式化
エネルギー原理であるHamiltonの原理やLagrangeの方程式を用いて有限要素法の定式化も可能である.前と同様に図3に示すように,解析対象である棒,あるいは,梁の一部の長さ$l$の有限な要素を考える.これに対する運動エネルギー$E_T^{ij}$は,
\begin{eqnarray*}
2E_T^{ij} = \int_x\int_y\int_z\rho\left(\frac{\partial u}{\partial t}\right)^2dxdydz = \int_x\int_y\int_z\rho\left(\frac{\partial u}{\partial t}\right)^T\left(\frac{\partial u}{\partial t}\right)dxdydz = \int_x\rho A\left(\frac{\partial u}{\partial t}\right)^T\left(\frac{\partial u}{\partial t}\right)dx
\end{eqnarray*}
であり,式(\ref{eqn:3001})より,
\begin{equation}
\frac{\partial u}{\partial t} = \left\{\begin{array}{cc} 1-\frac{x}{l} & \frac{x}{l}\end{array}\right\}\left\{\begin{array}{c} \frac{du_i\left(t\right)}{dt} \\ \frac{du_j\left(t\right)}{dt} \end{array}\right\}=\mathbf{N}\left(x\right)\left\{\begin{array}{c} \frac{du_i\left(t\right)}{dt} \\ \frac{du_j\left(t\right)}{dt} \end{array}\right\} \label{eqn:337}
\end{equation}
となるので,
\begin{eqnarray*}
2E_T^{ij} &=& \left\{\begin{array}{cc} \frac{du_i\left(t\right)}{dt} & \frac{du_j\left(t\right)}{dt} \end{array}\right\}\int_0^l\rho A\mathbf{N}\left(x\right)^T\mathbf{N}\left(x\right)dx\left\{\begin{array}{c} \frac{du_i\left(t\right)}{dt} \\ \frac{du_j\left(t\right)}{dt} \end{array}\right\} \\
&=& \left\{\begin{array}{cc} \frac{du_i\left(t\right)}{dt} & \frac{du_j\left(t\right)}{dt} \end{array}\right\}\int_0^l\rho A\left\{\begin{array}{c} 1-\frac{x}{l} \\ \frac{x}{l}\end{array}\right\}\left\{\begin{array}{cc} 1-\frac{x}{l} & \frac{x}{l}\end{array}\right\}dx\left\{\begin{array}{c} \frac{du_i\left(t\right)}{dt} \\ \frac{du_j\left(t\right)}{dt} \end{array}\right\} \\
&=& \left\{\begin{array}{cc} \frac{du_i\left(t\right)}{dt} & \frac{du_j\left(t\right)}{dt} \end{array}\right\}\int_0^l\rho A\displaystyle{\left[\begin{array}{cc} \left(1-\frac{x}{l}\right)^2 & \frac{x}{l}\left(1-\frac{x}{l}\right) \\
\frac{x}{l}\left(1-\frac{x}{l}\right) & \left(\frac{x}{l}\right)^2 \end{array}\right]}dx\left\{\begin{array}{c} \frac{du_i\left(t\right)}{dt} \\ \frac{du_j\left(t\right)}{dt} \end{array}\right\} \\
&=& \left\{\begin{array}{cc} \frac{du_i\left(t\right)}{dt} & \frac{du_j\left(t\right)}{dt} \end{array}\right\}\displaystyle{\left[\begin{array}{cc} \frac{\rho Al}{3} & \frac{\rho Al}{6} \\
\frac{\rho Al}{6} & \frac{\rho Al}{3} \end{array}\right]}\left\{\begin{array}{c} \frac{du_i\left(t\right)}{dt} \\ \frac{du_j\left(t\right)}{dt} \end{array}\right\} = \left\{\begin{array}{cc} \frac{du_i\left(t\right)}{dt} & \frac{du_j\left(t\right)}{dt} \end{array}\right\}\mathbf{M}_{ij}\left\{\begin{array}{c} \frac{du_i\left(t\right)}{dt} \\ \frac{du_j\left(t\right)}{dt} \end{array}\right\}
\end{eqnarray*}
一方,歪エネルギー$E_V^{ij}$は,
\begin{eqnarray*}
2E_V^{ij} &=& \int_x\int_y\int_z\sigma_{xx}\varepsilon_{xx}dxdydz = \int_x\int_y\int_z\left(\varepsilon_{xx}\right)^TE\varepsilon_{xx}dxdydz \\
&=& \left\{\begin{array}{cc} u_i & u_j \end{array}\right\}
\int_0^l\mathbf{B}^TEA\mathbf{B}dx\left\{\begin{array}{c} u_i \\ u_j \end{array}\right\} \\
&=& \left\{\begin{array}{cc} u_i & u_j \end{array}\right\}
\int_0^lEA\left\{\begin{array}{c} -\frac{1}{l} \\ \frac{1}{l}\end{array}\right\}
\left\{\begin{array}{cc} -\frac{1}{l} & \frac{1}{l}\end{array}\right\}dx
\left\{\begin{array}{c} u_i \\ u_j \end{array}\right\} \\
&=&\left\{\begin{array}{cc} u_i & u_j \end{array}\right\}\int_0^lEA
\left[\begin{array}{cc} \frac{1}{l^2} & -\frac{1}{l^2} \\
-\frac{1}{l^2} & \frac{1}{l^2}\end{array} \right]dx
\left\{\begin{array}{c} u_i\left(t\right) \\ u_j\left(t\right) \end{array}\right\} \\
&=&\left\{\begin{array}{cc} u_i & u_j \end{array}\right\}
\left[\begin{array}{cc} \frac{EA}{l} & -\frac{EA}{l} \\
-\frac{EA}{l} & \frac{EA}{l}\end{array} \right]
\left\{\begin{array}{c} u_i\left(t\right) \\ u_j\left(t\right) \end{array}\right\}
=\left\{\begin{array}{cc} u_i & u_j \end{array}\right\}
\mathbf{K}_{ij}\left\{\begin{array}{c} u_i\left(t\right) \\ u_j\left(t\right) \end{array}\right\}
\end{eqnarray*}
従って,一般座標を$u_i$,$u_j$,節点に作用する内力$f_i\left(t\right)$,$f_j\left(t\right)$を一般力と見なし,Lagrange関数
\begin{eqnarray*}
L^{ij} = E_T^{ij} - E_V^{ij}
\end{eqnarray*}
を考えると,次のLagrange方程式
\begin{eqnarray*}
&& \frac{d}{dt}\left(\frac{\partial L^{ij}}{\partial\dot{u}_i}\right) + \frac{\partial L^{ij}}{\partial u_i} = - f_i\left(t\right) \\
&& \frac{d}{dt}\left(\frac{\partial L^{ij}}{\partial\dot{u}_j}\right) + \frac{\partial L^{ij}}{\partial u_j} = f_j\left(t\right)
\end{eqnarray*}
により,次のような要素に対する基礎方程式を求めることができる.
\begin{eqnarray*}
\mathbf{M}_{ij}\left\{\begin{array}{c} \frac{d^2u_i\left(t\right)}{dt^2} \\ \frac{d^2u_j\left(t\right)}{dt^2} \end{array}\right\}+ \mathbf{K}_{ij}\left\{\begin{array}{c} u_i\left(t\right) \\ u_j\left(t\right) \end{array}\right\} = \left\{\begin{array}{c} -f_i\left(t\right) \\ f_j\left(t\right) \end{array}\right\}
\end{eqnarray*}
前と同様,節点変位ベクトル
\begin{eqnarray*}
\mathbf{u}\left(t\right)=\left\{\begin{array}{cccc} u_0\left(t\right), & u_1\left(t\right) & \ldots, & u_N\left(t\right)\end{array}\right\}^T
\end{eqnarray*}
および,各節点に加わる外力ベクトル
\begin{eqnarray*}
\mathbf{f}\left(t\right)=\left\{\begin{array}{cccc} f_0\left(t\right), & f_1\left(t\right) & \ldots, & f_N\left(t\right)\end{array}\right\}^T
\end{eqnarray*}
を考えることにより,系全体に対する次のような基礎方程式が得られる.
\begin{eqnarray*}
\mathbf{M}\frac{d^2\mathbf{u}\left(t\right)}{dt^2} + \mathbf{K}\mathbf{u}\left(t\right) = \mathbf{f}\left(t\right)
\end{eqnarray*}
本定式化でわかるように,質量行列と剛性行列は,系の運動エネルギー,歪エネルギーを定めることにより求めることができ,定められた行列により,節点変位ベクトルに対する2階の常微分方程式形で表現すれば良いことがわかる.
3.1.3 プログラミング例
以上の定式化に基づき,有限要素データを読み込み,全体質量行列$\mathbf{M}$,全体剛性行列$\mathbf{K}$を求めるプログラムを考える.基本的な流れを示すプログラムを以下に示す.プログラム中にコメントしてあるように,次のような流れで計算を進めている.
3.2 2次元弾性解析
3.2.1 定ひずみ三角形要素
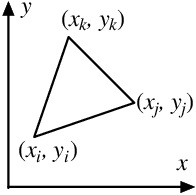
図 3.2 Finite element of a plane
2次元問題においても考え方は,同様で,解析領域を分割して定められる,例えば,図3.2に示すような三角形形状の有限な要素に節点($x_i$, $y_i$),($x_j$, $y_j$),($x_k$, $y_k$)を定め,その要素内任意点の変位と節点変位の関係を形状関数を用いて定義し,応力-歪関係,歪と変位の関係を使用する.$xy$平面の面内変形だけを考える場合,$x$軸,$y$軸方向変位を$u$,$v$とした場合,次のように一次関数で置くことができる(一定ひずみ要素).
\begin{eqnarray*}
\left.\begin{array}{l}
u\left(x, y, t\right) = a_0\left(t\right) + a_1\left(t\right)x + a_2\left(t\right)y \\
v\left(x, y, t\right) = b_0\left(t\right) + b_1\left(t\right)x + b_2\left(t\right)y
\end{array}\right\}
\end{eqnarray*}
各節点座標における変位成分を($u_i$, $v_i$),($u_j$, $v_j$),($u_k$, $v_k$)とすると,
\begin{eqnarray*}
&& \left.\begin{array}{l}
u\left(x_i, y_i, t\right) = u_i\left(t\right) = a_0\left(t\right) + a_1\left(t\right)x_i + a_2\left(t\right)y_i \\
u\left(x_j, y_j,t \right) = u_j\left(t\right) = a_0\left(t\right) + a_1\left(t\right)x_j + a_2\left(t\right)y_j \\
u\left(x_k, y_k,t \right) = u_k\left(t\right) = a_0\left(t\right) + a_1\left(t\right)x_k + a_2\left(t\right)y_k
\end{array}\right\} \\
&& \left.\begin{array}{l}
v\left(x_i, y_i, t\right) = v_i\left(t\right) = b_0\left(t\right) + b_1\left(t\right)x_i + b_2\left(t\right)y_i \\
v\left(x_j, y_j, t\right) = v_j\left(t\right) = b_0\left(t\right) + b_1\left(t\right)x_j + b_2\left(t\right)y_j \\
v\left(x_k, y_k, t\right) = v_k\left(t\right) = b_0\left(t\right) + b_1\left(t\right)x_k + b_2\left(t\right)y_k
\end{array}\right\}
\end{eqnarray*}
ここで,$a_i\left(t\right)$, $b_i\left(t\right)$($i=0$, $1$, $2$)は,節点座標と節点変位で次のように定めることができる.まず,行列表示すると
\begin{eqnarray*}
&& \left\{\begin{array}{c} u_i\left(t\right) \\ u_j\left(t\right) \\ u_k\left(t\right) \end{array}\right\}
=\left[\begin{array}{ccc}
1 & x_i & y_i \\
1 & x_j & y_j \\
1 & x_k & y_k \end{array}\right]
\left\{\begin{array}{c} a_0\left(t\right) \\ a_1\left(t\right) \\ a_2\left(t\right)
\end{array}\right\} \\
&& \left\{\begin{array}{c} v_i\left(t\right) \\ v_j\left(t\right) \\ v_k\left(t\right) \end{array}\right\}
=\left[\begin{array}{ccc}
1 & x_i & y_i \\
1 & x_j & y_j \\
1 & x_k & y_k \end{array}\right]
\left\{\begin{array}{c} b_0\left(t\right) \\ b_1\left(t\right) \\ b_2\left(t\right)
\end{array}\right\}
\end{eqnarray*}
よって,
\begin{eqnarray*}
&& \left\{\begin{array}{c} a_0\left(t\right) \\ a_1\left(t\right) \\ a_2\left(t\right) \end{array}\right\}
=\frac{1}{2\Delta}\left[\begin{array}{ccc}
x_jy_k - x_ky_j & x_ky_i - x_iy_k & x_iy_j - x_jy_i \\
y_j-y_k & y_k - y_i & y_i - y_i \\
x_k - x_j & x_i - x_k & x_j - x_i \end{array}\right]
\left\{\begin{array}{c} u_i\left(t\right) \\ u_j\left(t\right) \\ u_k\left(t\right)
\end{array}\right\}
= \left[\begin{array}{ccc}
a_{jk} & a_{ki} & a_{ij} \\
b_{jk} & b_{ki} & b_{ij} \\
c_{jk} & c_{ki} & c_{ij}\end{array}\right]\left\{\begin{array}{c} u_i\left(t\right) \\ u_j\left(t\right) \\ u_k\left(t\right)
\end{array}\right\} \\
&& \left\{\begin{array}{c} b_0\left(t\right) \\ b_1\left(t\right) \\ b_2\left(t\right) \end{array}\right\}
=\frac{1}{2\Delta}\left[\begin{array}{ccc}
x_jy_k - x_ky_j & x_ky_i - x_iy_k & x_iy_j - x_jy_i \\
y_j-y_k & y_k - y_i & y_i - y_i \\
x_k - x_j & x_i - x_k & x_j - x_i \end{array}\right]
\left\{\begin{array}{c} v_i\left(t\right) \\ v_j\left(t\right) \\ v_k\left(t\right)
\end{array}\right\} = \left[\begin{array}{ccc}
a_{jk} & a_{ki} & a_{ij} \\
b_{jk} & b_{ki} & b_{ij} \\
c_{jk} & c_{ki} & c_{ij}\end{array}\right]\left\{\begin{array}{c} v_i\left(t\right) \\ v_j\left(t\right) \\ v_k\left(t\right)
\end{array}\right\}
\end{eqnarray*}
ここで,$\Delta$は,三角形要素の面積であり,次式となる.
\begin{eqnarray*}
2\Delta = \left | \begin{array}{ccc}
1 & x_i & y_i \\
1 & x_j & y_j \\
1 & x_k & y_k
\end{array}\right|
\end{eqnarray*}
また,
\begin{eqnarray*}
\left. \begin{array}{l}
\displaystyle{a_{lm} = \frac{x_ly_m - y_mx_l}{2\Delta}} \\
\displaystyle{b_{lm} = \frac{y_l - y_m}{2\Delta}} \\
\displaystyle{c_{lm} = \frac{x_m-x_l}{2\Delta}}\\
(l, m=i, j, k)
\end{array}\right\}
\end{eqnarray*}
よって,要素内任意点の変位は,次のように表わすことができる.
\begin{eqnarray*}
&& u = u\left(x,y,t\right) =
\left\{\begin{array}{ccc}
1 & x & y \end{array}\right\}
\left[\begin{array}{ccc}
a_{jk} & a_{ki} & a_{ij} \\
b_{jk} & b_{ki} & b_{ij} \\
c_{jk} & c_{ki} & c_{ij}
\end{array}\right]
\left\{\begin{array}{c}
u_i\left(t\right) \\ u_j\left(t\right) u_k\left(t\right)
\end{array}\right\} \\
&& v = v\left(x,y,t\right) =
\left\{\begin{array}{ccc}
1 & x & y \end{array}\right\}
\left[\begin{array}{ccc}
a_{jk} & a_{ki} & a_{ij} \\
b_{jk} & b_{ki} & b_{ij} \\
c_{jk} & c_{ki} & c_{ij}
\end{array}\right]
\left\{\begin{array}{c}
v_i\left(t\right) \\ v_j\left(t\right) v_k\left(t\right)
\end{array}\right\}
\end{eqnarray*}
変位ベクトル$\mathbf{u}$としてまとめると,
\begin{eqnarray*}
\mathbf{u} &=&
\left\{\begin{array}{c} u\left(x,y,t\right) \\ v\left(x,y,t\right) \end{array}\right\} =
\left[\begin{array}{cccccc}
1 & 0 & x & 0 & y & 0 \\
0 & 1 & 0 & x & 0 & y \end{array}\right]
\left[\begin{array}{cccccc}
a_{jk} & 0 & a_{ki} & 0 & a_{ij} & 0 \\
0 & a_{jk} & 0 & a_{ki} & 0 & a_{ij} \\
b_{jk} & 0 & b_{ki} & 0 & b_{ij} & 0 \\
0 & b_{jk} & 0 & b_{ki} & 0 & b_{ij} \\
c_{jk} & 0 & c_{ki} & 0 & c_{ij} & 0 \\
0 & c_{jk} & 0 & c_{ki} & 0 & c_{ij}
\end{array}\right]
\left\{\begin{array}{c}
u_i\left(t\right) \\ v_i\left(t\right) \\ u_j\left(t\right) \\ v_j\left(t\right) \\ u_k\left(t\right) \\ v_k\left(t\right)
\end{array}\right\} \\
&=& \mathbf{N}\left(x,y\right)
\left\{\begin{array}{c}
u_i\left(t\right) \\ v_i\left(t\right) \\ u_j\left(t\right) \\ v_j\left(t\right) \\ u_k\left(t\right) \\ v_k\left(t\right)
\end{array}\right\}
\end{eqnarray*}
次に歪ベクトルを計算する.歪成分は,
\begin{equation}
\left\{\varepsilon\right\} = \left\{\begin{array}{c}
\varepsilon_x \\ \varepsilon_y \\ \gamma_{xy} \end{array}\right\} = \left\{\begin{array}{c}
\frac{\partial u}{\partial x} \\ \frac{\partial v}{\partial y} \\ \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}
\end{array}\right\}
\end{equation}
ここで,次の関係が成立している.
\begin{eqnarray*}
&& \frac{\partial u}{\partial x} = \frac{1}{2\Delta}\left(b_iu_i + b_ju_j + b_mu_m\right) \\
&& \frac{\partial v}{\partial y} = \frac{1}{2\Delta}\left(c_iv_i + v_jv_j + c_mv_m\right) \\
&& \frac{\partial u}{\partial y}+\frac{\partial v}{\partial x} = \frac{1}{2\Delta}\left(c_iu_i + b_iv_i + c_ju_j + b_jv_j + c_mu_m+b_mv_m\right)
\end{eqnarray*}
よって,歪ベクトル$\left\{\varepsilon\right\}$と節点変位ベクトル$\left\{\begin{array}{llllll}u_i & v_i & u_j & v_j & u_m & v_m \end{array}\right\}^T$との関係は次のようになる.
\begin{equation}
\left\{\varepsilon\right\} = \frac{1}{2\Delta}\left[\begin{array}{cccccc}
b_i & 0 & b_j & 0 & b_m & 0 \\
0 & c_i & 0 & c_j & 0 & c_m \\
c_i & b_i & c_j & b_j & c_m & b_m
\end{array} \right]
\left\{\begin{array}{l}u_i \\ v_i \\ u_j \\ v_j \\ u_m \\ v_m \end{array}\right\}
\equiv \left[\mathbf{B}\right]
\left\{\begin{array}{l}u_i \\ v_i \\ u_j \\ v_j \\ u_m \\ v_m \end{array}\right\}
\end{equation}
応力−歪関係は次のように表現できる.
\begin{equation}
\left\{\sigma\right\} = \left\{\begin{array}{c}
\sigma_x \\ \sigma_y \\ \tau_{xy}
\end{array} \right\} = \left[\mathbf{D}\right]
\left\{\begin{array}{c}
\varepsilon_x \\ \varepsilon_y \\ \gamma_{xy} \end{array}\right\}
=\left[\mathbf{D}\right]\left\{\varepsilon\right\}
\end{equation}
ここで,等方弾性体に対する平面応力問題($\sigma_z=0$)では,
\begin{eqnarray*}
\left[\mathbf{D}\right] = \frac{E}{1-\nu^2}\left[\begin{array}{ccc}
1 & \nu & 0 \\
\nu & 1 & 0 \\
0 & 0 & \frac{1-\nu}{2}
\end{array}\right]
\end{eqnarray*}
また,平面歪問題($\varepsilon_z=0$)では,
\begin{eqnarray*}
\left[\mathbf{D}\right] = \frac{E\left(1-\nu\right)}{2\left(1+\nu\right)\left(1-2\nu\right)}
\left[\begin{array}{ccc}
1 & \frac{\nu}{1-\nu} & 0 \\
\frac{\nu}{1-\nu} & 1 & 0 \\
0 & 0 & \frac{1-2\nu}{2\left(1-\nu\right)}
\end{array}\right]
\end{eqnarray*}
よって,歪エネルギー$E_V$を求めると次式となる.
\begin{eqnarray*}
E_V = \int_V \frac12\left\{\varepsilon\right\}^T\left\{\sigma\right\}dV
= \int_V\frac12\left\{\sigma\right\}^T\left\{\varepsilon\right\}dV
\end{eqnarray*}
従って,第一変分を取ると次のようになる.
\begin{eqnarray}
\delta E_V &=& \int_V\delta\left\{\varepsilon\right\}^T \left[\mathbf{D}\right]\left\{\varepsilon\right\}dV
= \delta\left\{\begin{array}{llllll}u_i & v_i & u_j & v_j & u_m & v_m \end{array}\right\}
\int_V\left[\mathbf{B}\right]^T\left[\mathbf{D}\right]\left[\mathbf{B}\right]dV
\left\{\begin{array}{l}u_i \\ v_i \\ u_j \\ v_j \\ u_m \\ v_m \end{array}\right\} \nonumber\\
&\equiv& \delta\left\{\begin{array}{llllll}u_i & v_i & u_j & v_j & u_m & v_m \end{array}\right\}
\left[\mathbf{K}\right]
\left\{\begin{array}{l}u_i \\ v_i \\ u_j \\ v_j \\ u_m \\ v_m \end{array}\right\}
\end{eqnarray}
ここで,三角形の積分を考え,解析対象の厚さ(z方向)を$t$とすると,
\begin{eqnarray*}
\left[\mathbf{K}\right\}=\int_V\left[\mathbf{B}\right]^T\left[\mathbf{D}\right]\left[\mathbf{B}\right]dV
=\left[\mathbf{B}\right]^T\left[\mathbf{D}\right]\left[\mathbf{B}\right]t\Delta
\end{eqnarray*}
となる.一方,運動エネルギー$E_T$は,
\begin{eqnarray*}
E_T = \int_V \frac12\rho\left\{\begin{array}{ll} \dot{u} & \dot{v} \end{array}\right\}
\left\{\begin{array}{l} \dot{u} \\ \dot{v} \end{array}\right\}
\end{eqnarray*}
従って,第一変分をとると次のようになる.
\begin{eqnarray}
\delta E_T &=& \int_V \rho\delta\left\{\begin{array}{ll} \dot{u} & \dot{v} \end{array}\right\}
\left\{\begin{array}{l} \dot{u} \\ \dot{v} \end{array}\right\}
=\delta\left\{\begin{array}{llllll}\dot{u}_i & \dot{v}_i & \dot{u}_j & \dot{v}_j & \dot{u}_m & \dot{v}_m \end{array}\right\}\left[\mathbf{N}\right]^T\left[\mathbf{N}\right]
\left\{\begin{array}{l}\dot{u}_i \\ \dot{v}_i \\ \dot{u}_j \\ \dot{v}_j \\ \dot{u}_m \\ \dot{v}_m \end{array}\right\} \nonumber\\
&\equiv& \delta\left\{\begin{array}{llllll}\dot{u}_i & \dot{v}_i & \dot{u}_j & \dot{v}_j & \dot{u}_m & \dot{v}_m \end{array}\right\}
\left[\mathbf{M}\right]
\left\{\begin{array}{l}\dot{u}_i \\ \dot{v}_i \\ \dot{u}_j \\ \dot{v}_j \\ \dot{u}_m \\ \dot{v}_m \end{array}\right\}
\end{eqnarray}
ここで,解析対象の厚さ(z方向)を$t$とすると,
\begin{eqnarray*}
\left[\mathbf{M}\right\}=\int_x\int_y\rho\left[\mathbf{N}\right]^T\left[\mathbf{N}\right]dxdy\cdot t
\end{eqnarray*}
となる.
3.2.2 線形ひずみ三角形要素
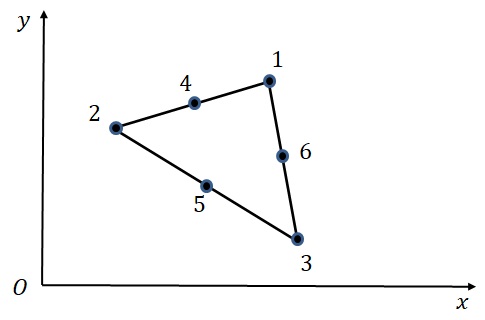
図 3.3 Finite element of a plane
内部のひずみ分布を考慮するために,図3.3に示すような頂点と辺の中点に節点をもつ三角形要素を考える.節点番号を図に示すように,反時計回りに頂点に1,2,3,次に辺の中点に4,5,6とつける.一つの節点$i$で,前節の定ひずみ要素と同様に変位成分$u_i$と$v_i$をもつとする.したがって,要素の5節点に関する変位成分は,次式のようになる.
\begin{eqnarray*}
\left\{\delta\right\}^T = \left\{\begin{array}{ccccccc}
u_1& v_1& u_2 & v_2& \ldots & u_6 & v_6 \end{array}\right \}
\end{eqnarray*}
要素の変位場をこの節点変位を用いて表現することになるので,任意点の変位は次式のように表現できることになる.
\begin{eqnarray*}
\left. \begin{array}{l}
u= \alpha_1 + \alpha_2x + \alpha_3y + \alpha_4x^2 + \alpha_5xy + \alpha_6y^2 \\
v= \beta_1 + \beta_2x + \beta_3y + \beta_4x^2 + \beta_5xy + \beta_6y^2 \\
\end{array}\right\}
\end{eqnarray*}
上式に現れる12個の未定係数$\alpha_i$,$\beta_i$$(i=1,2,\ldots,6)$を12個の節点変位$u_i$,$v_i$で表現することになる.以下,形式的に行列表現を用いることにする.この節点変位ベクトル$\left\{\delta\right\}$と未定係数ベクトル$\left\{\alpha\right\}$の関係は,各節点変位を上式に代入することにより,次式のように定まる.
\begin{eqnarray*}
\left\{\delta\right\} =\mathbf{H}\left\{\alpha\right\}
\end{eqnarray*}
この式を逆に解くと,未定係数ベクトル$\left\{\alpha\right\}$は,次式の形で節点変位ベクトル$\left\{\delta\right\}$と関係づけることができる.
\begin{eqnarray*}
\left\{\alpha\right\} =\mathbf{H}^{-1}\left\{\delta\right\}
\end{eqnarray*}
したがって,変位場は次式で表せることになる.
\begin{eqnarray*}
\left\{\begin{array}{l}
u \\ v \end{array}\right\}
&=&\left[ \begin{array}{cc} \mathbf{A} & \mathbf{0} \\
\mathbf{0} & \mathbf{A} \end{array} \right]\mathbf{H}^{-1}\left\{\delta\right\} \\
&=&\mathbf{N}\left\{\delta\right\}
\end{eqnarray*}
ここで,$\mathbf{A}$は次式となる.
\begin{eqnarray*}
\mathbf{A}=\left[\begin{array}{cccccc}1&x&y&x^2&xy&y^2\end{array}\right]
\end{eqnarray*}
この後は,前と同様に処理を行えば良いことになる.
3.3 演習問題
上記の形状関数$\mathbf{N}$により規定される節点変位と任意点変位の関係を使って,平面応力,および,平面歪を仮定した場合の質量行列$\mathbf{M}$と剛性行列$\mathbf{K}$を定式化せよ.