2.運動と振動の制御
2.1 乗物の移動制御
様々な機械システムが想定できるが,身近なものとしては自動車などの乗物がある.免許を取る必要はあるが,エンジンをかけ,アクセルを踏めば自動車は走り,ブレーキを踏めば止まるので,大概の人は,自動車を運転し,目的地に到着することができる.ヒトがどのように運転し,目的に到着するのかを実験的に調べたり,それを厳密にモデリングして挙動を調べてみることも面白いとは思うが,人間の動作・反応を定量的に入力として与えることや実際の自動車の動的な挙動を調べようと思うと余りに複雑なものになるので,ここでは,単純に力を加えて,自動車をある目標地点まで走らせる,という数値実験を試みる.
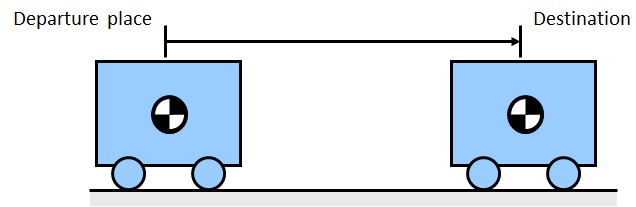
図2‐1 乗物による移動
図2-1に示すように乗物の質量が重心に集中していると仮定し,単純な直線運動をする1自由度系を考える.一般には,こういった移動に際しては,図2-2に示すような速度パターンにしたがって,移動する制御入力により運転が行われる.この際,移動距離はこの速度パターンで作られる面積となるので,移動距離を正確に与えて動かしてみてはどうかという考え方も起こる.
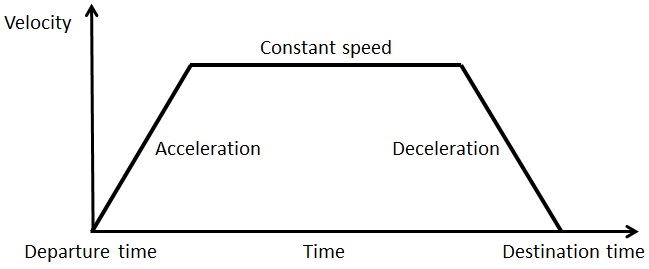
図2‐2 移動における速度パターン
そこで,図2-3左図に示すように,入力$f$を与えて,質量$M$の物体を$x_T$の距離移動させるという問題を考える.ブロック線図で表すと右図のようになる.プラントである物体に力$f$を与えて速度を生み出し,それをある時間続けて(積分することになる)最終的に$x$の変位となるが,これを目標とする移動距離$x_T$に持って行く,ということになる.この時の運動方程式は,Newtonの第2法則より次式となる.
\begin{eqnarray*}
M\ddot{x} =f
\end{eqnarray*}

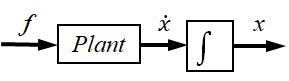
図2‐3 力$f$を加えて距離$x_T$移動させる課題
1.2 制御入力
駆動力である加える力$f$に関しては,(多分基礎制御などで色々学んでおり,その知識を使ってみたいという希望があると思うので)フィードバック制御系で構成される入力を考えてみる.取りあえず,図2-4に示すように,目標値に対する現在値との差に比例する入力,即ち,比例制御による駆動を考える.
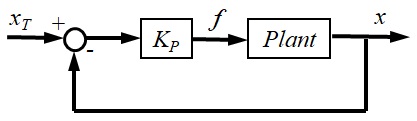
図2‐4 比例制御により距離$x_T$移動させる制御
即ち,時々刻々変化する乗物の時刻$t$における位置$x=x(t)$をセンサなどで計測し,その値と目標位置$x_T$との差を計算し,それを$K_P$倍したものを入力$f=f(t)$として与えるというものである.即ち,駆動力は次のように与えることになる.
\begin{eqnarray*}
f =f(t)=K_P\left\{x_T -x(t)\right\}
\end{eqnarray*}
$K_P$は比例ゲインと呼ばれる.また,運動方程式を考慮して,ブロック線図を書き換えると図2-5のようになる.

図2‐5 比例制御による物体の移動制御
この系に対する数値実験プログラムは,例えば,次のようになる.
【プログラム例】

このプログラムを用いて,数値実験を行い,結果について考察せよ.また,結果が正しいかどうか他の方法での結果と比較してみよ.
比例制御では,どのような比例ゲイン$K_P$を与えてもうまく行かないので,次のように微分制御も加えてみることにする.
\begin{eqnarray*}
f =f(t)=K_P\left\{x_T -x(t)\right\}+K_D\left\{v_T-v(t)\right\}
\end{eqnarray*}
比例制御は,P制御と呼ばれ,比例・微分制御は,PD制御と呼ばれ,$K_D$は微分制御に関するゲインである.この系の場合のブロック線図は図2-6のようになる.
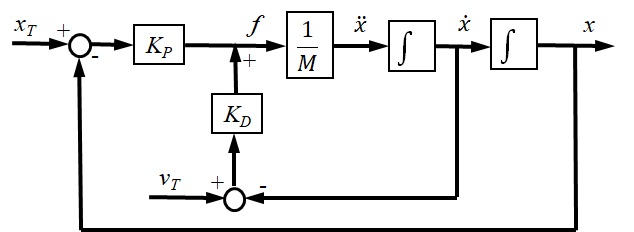
図2‐6 比例・微分制御による物体の移動制御
前述のプログラム例を書き直して,比例・微分制御に基づく入力を用いた場合について数値実験を行ってみよ.目標速度$v_T$は,この場合最終的に停止するので,$v_T=0$として良い.また,各ゲインの影響について調べてみよ.
2.3 サーボ機構
サーボ機構とは機械の動く変位や速度といった出力変数を入力変数に忠実に自動的に動かそうとする制御系であり,自動制御,制御工学分野における概念ではあるが,基本的に機械は動く,動かす場合が殆んどであるので,機械システムに携わるものは必ず知っておくべき概念と思われる.今回考えた制御を含む機械システムは,サーボ機構となる.サーボ機構はいくつかの基本的な構成が考えられるが,その基本的な動作はブロック線図で表現することができる.簡単なブロック線図をを図2-7に示す.サーボ機構の前向き要素は二つ(あるいは三つ)に分解される.制御対象は制御される機械によって特性が決まり,勝手に決めて良いものではない.制御対象のうち駆動機器に関しては多少選択の自由があるが,それも選択したものに応じた特性を考える必要がある.
それに対し補償増幅器は設計時に自由に選ぶことができると考えてよい.これは誤差信号$e(t)$を増幅するだけでなく,制御系全体の性能が要求された性能を満足するように操作信号$i(t)$を作る.検出器は入出力信号を検出し,誤差信号を作り出す.
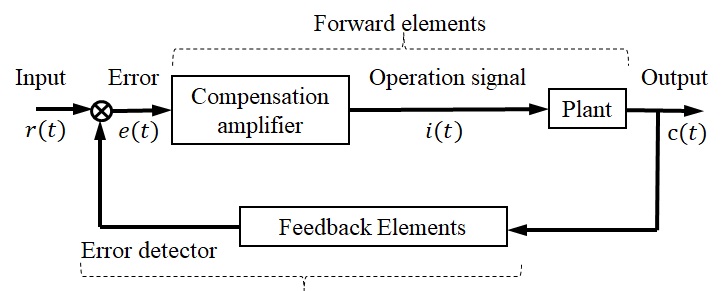
図2‐7 基本的なサーボ機構
演習
図2-8は,重心軸回りの慣性モーメントが$J_M$に回転トルク$T$を加え,回転体を$\theta$回転させる系を表している.任意角度(例えば,60度)回転させるための入力トルクを比例・微分制御で生成した場合の数値実験を行い,系の応答を計算し,結果について考察せよ.パラメータ値は,自分たちで決めて良い.
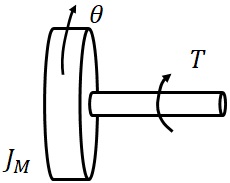
図2‐8 回転運動










