3.振動制御モデル例
3.1 モデリングと基礎理論
対象のモデル化を行う際には,基礎となる理論やそこでの仮定を十分に理解しておくことが重要である.機械工学は,"Mechanical Engineering"であり,その基礎理論は,"Mechanics"である.メカニクスは,”力学”であるが,力学関連科目としては,
Mechanics
力学問題全般を対象とする学問
狭義に静的問題(Statics)を対象とする場合もある
Dynamics
動力学
力などの要因に伴う動的変化を対象とした学問
Kinetics
運動学,動力学
運動の変化そのものを対象とする学問
また,機械工学に関連した”力学”の概念的な分類を図3-1に示す.質点系,剛体系,弾性体系など固体力学関連だけでなく,熱流体系の力学系を表示しており,作用力・発生力を外的・内的で区別したり,静的・動的を固定・移動系という表現で区別している.この図から分かるように,より現実の現象を反映したモデリングを行うためには,多くの基礎理論を理解する必要がある.機械工学科学士の称号を有する場合は,これらの殆んどの内容にどこかで触れている(と思われる)ので,本講義では各理論における仮定を確認しながら,進めることにする.
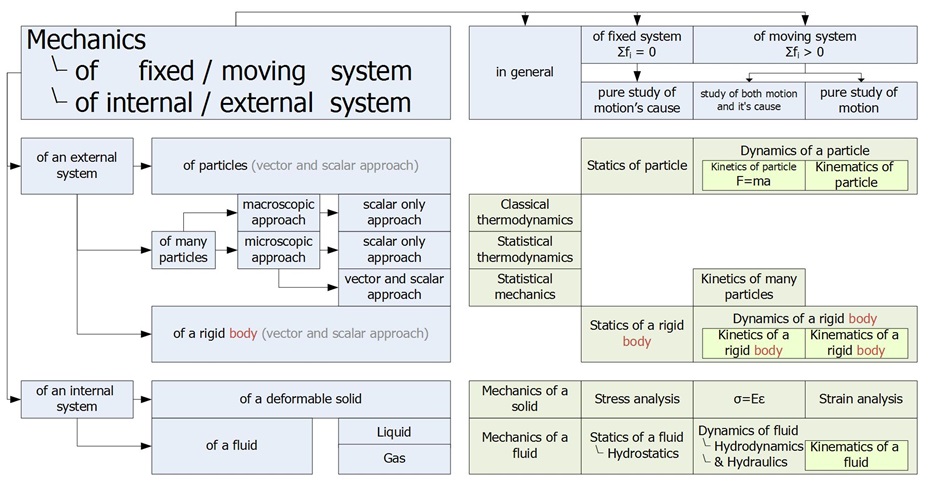
図3-1 力学関連図
3.2 1自由度モデルにおける仮定
前回取り上げた図3-2に示す1自由度モデルを考える.”乗物の質量が重心に集中していると仮定し,単純な直線運動をする1自由度系を考える”としたが,実際には以下に示すような仮定を置いている.
【仮定】
座標系:慣性座標系と仮定.
$x(t)$ : 定義した座標系に基準を持つ物体の変位.
車輪の質量:乗物に対して無視できると仮定.
車輪のベアリング摩擦:乗物の運動に対して無視できるほど小さいと仮定.
作用力$f(t)$:符号もう含め,定義した$x(t)$と同方向に作用すると仮定.
$M$:乗物全体の質量で一定であると仮定.
乗物の運動:水平方向のみに運動すると仮定.回転しないと仮定.車輪は路面から離れないと仮定.
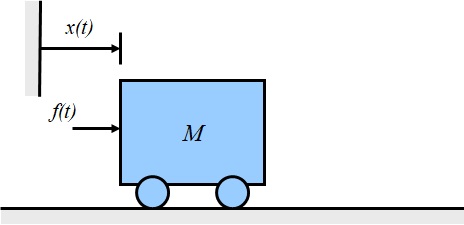
図3-2 1自由度系モデル
この系にばねとダシュポットを加えた1自由度粘性振動系とした場合のモデル化について考える.追加される仮定としては,ばね要素と減衰要素を使う場合の常道的なものである以下の3つが考えられる.
【仮定】
弾性変形:Hookeの法則が成り立つと仮定.
減衰特性:粘性減衰系を仮定.
基準位置:系の平衡状態と仮定(この系の場合は,ばねは自然長できまる位置)
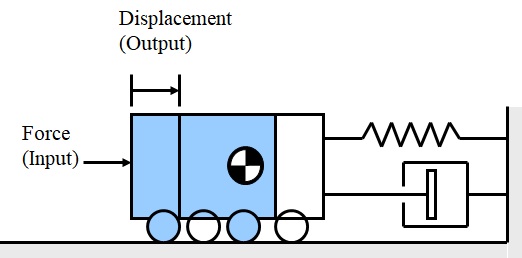
図3-3 1自由度粘性減衰振動系モデル
質量,ばね,ダシュポットでモデル化すると自ずと,作用力$f(t)$を含め,これらに起因した”力”を想定する必要がある.連結部,接触部と意識してFree-body Diagraを描くと例えば,図3-4(a)のようになる.重力$W$が乗物の重心位置に作用しており,車輪を介して地面と接していることから反力$R_1$,$R_2$を車輪位置で表している.また,ばね,ダッシュポットの方向は,
【仮定】
符号:引張力が作用する場合を正と仮定.
により,方向を正方向として記述している.ここで,路面と車輪の接触点における反力を考えたが,車輪回転までも考慮した場合に作用する力を描くと,例えば,図3-4(b)のようになる.これらの力は,前に掲げた仮定
【仮定】
車輪の質量:乗物に対して無視できると仮定.
車輪のベアリング摩擦:乗物の運動に対して無視できるほど小さいと仮定.
により,”ここでは”考える必要が無いことになる.
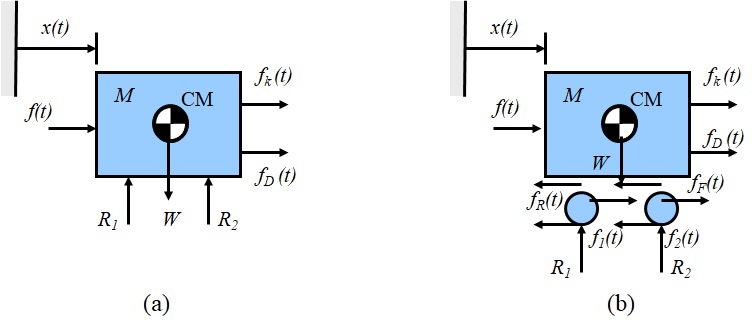
図3-4 1自由度粘性減衰振動系に対するFree-body Diagram
作用力$f(t)$の作用点について,何も述べていなかったが,ここでは,前置きの通り,
【仮定】
乗物の質量:重心に集中していると仮定
の仮定があるので,作用点は,重心位置ということになる.しかし,前後輪の接触点を考えると実際には,後輪駆動の場合は,図3-5のように作用すると考えるべきと思われる.力は,作用点がどの位置に来るかで対象に対する”効果”に変化が生じる場合がある(力の三要素に作用点が加えてあるのはそのため).即ち,Free-body Diagram記述に際しては,加わる力(作用力)やそのに伴い連結部,接合部で発生する作用・反作用の方向,作用点などをきちんとイメージ化し,解析したい対象の物理現象との対応付けを必ず行うことが求められる.
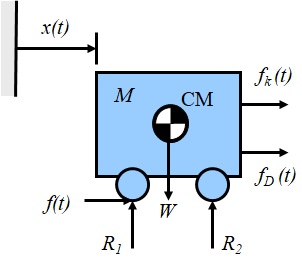
図3-5 駆動力を考慮した1自由度粘性減衰振動系に対するFree-body Diagram
3.3 自動車発進時の挙動
作用力が起因して発生する挙動について,数値実験により調べてみることにする.図3-6(a)に示す自動車を(b)に示すような前後輪を上下方向ばねで支持された剛体モデルでモデル化する.ここで,車体質量$M=1600$kg, 車体重心回りの慣性モーメント$J=mR^2=2304$kg$\cdot$m$^2$とし,重心から前後輪の接地点までの水平方向距離はそれぞれ,$l_=1.3$m,$l_2=1.7$m,また,前後輪のタイヤ・サスペンション部のばね定数はそれぞれ,$k_1=3.92\times10^4$N/m, $k_2=4.41\times10^4$N/mとする(以前,機械力学で学んだ演習問題で使用した値である).また,図3-6に示すように前輪駆動での走行を想定し,路面接地点から重心までの鉛直方向距離(高さ)は$h=0.6$mとすることにする.

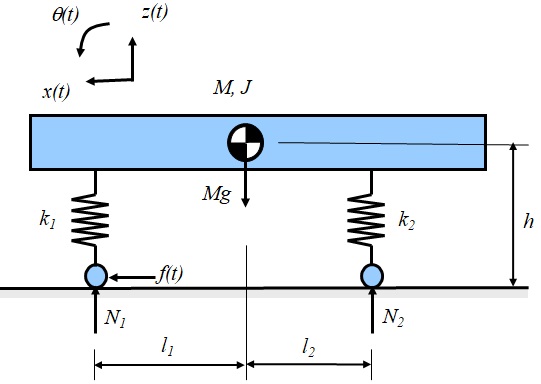
(a) (b)
図3-6 自動車走行モデル例
3.4 演習
図3-6(b)に示すように,進行方向に$x(t)$,鉛直方向に$z(t)$座標を取り,反時計回りの回転角(ピッチ角)を$\theta$として,運動方程式を求め,一定加速,例えば,$f(t)=1.6$kNで走行した場合の発進時10秒間の系の挙動を調べよ.
この系に対する数値実験プログラムは,例えば,次のようになる.
【プログラム例】

図3-7 プログラム例
このプログラムを用いて,車体の走行速度,上下方向変位,ピッチング角の時刻歴応答は例えば次のようになる.
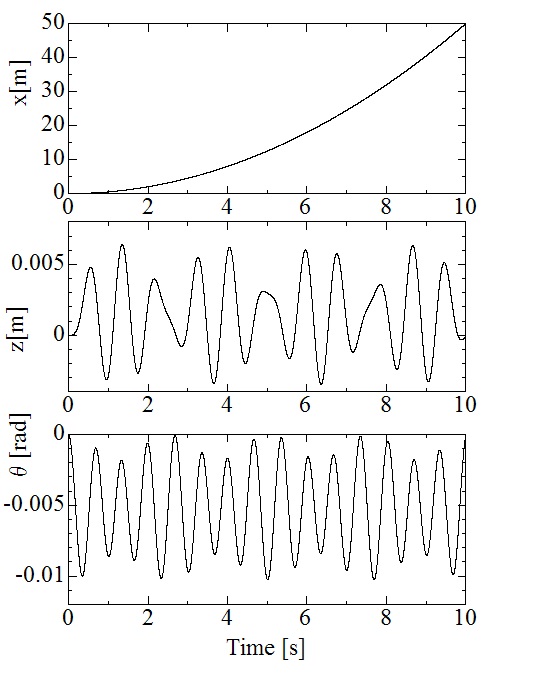
図3-8 計算例









