4.センサのモデル化
サーボ機構のように,機械の動く変位や速度といっ物理量を使って駆動(制御)する機械システムでは,当然の如く時間的に変化する変位,速度を計測する必要がある.即ち,機械システム内にセンサを配して,必要が物理量をリアルタイムで計測する必要がある.ここでは,機械システムの動的挙動を制御するために必要な物理量を計測するセンサの動特性を考えると共にそれがシステム全体に対する影響について考察する.
4.1 ジャイロセンサ
航空機や船舶等の自律航法に利用される物体の角度(姿勢)や角速度あるいは角加速度を検出するセンサである,ジャイロスコープ(gyroscope),ジャイロセンサの用途は広がって来ており,近年では,カーナビゲーションや自動運転システム,ロボット,スマートフォン,デジタルカメラなど身近な機器にも使用されるようになってきている.小型化も進み様々な方式の物が存在するが,ここでは,運動学的に興味深い回転型の動特性について考える.
回転型のジャイロセンサの基本的な構造を図4-1に示す.円筒形状ローターをジンバルと呼ばれる容器に設けた軸受で支持し,角速度$\Omega$で(高速)回転させる.ローターを含むジンバル自体も回転自由に基礎台上に支持されており,右端は,ばねとダシュポットで支えられている.図に示すように,基礎台全体が,垂直上向きの入力軸回りに角速度$\omega(t)$で回転運動を始めるとジンバルを支えている軸回りの回転角変位$\theta(t)$が発生し,この回転角度に比例した信号(電圧信号)を検出することにより,基礎台を取りつけた物体に発生している角速度$\omega(t)$を検出するセンサである.
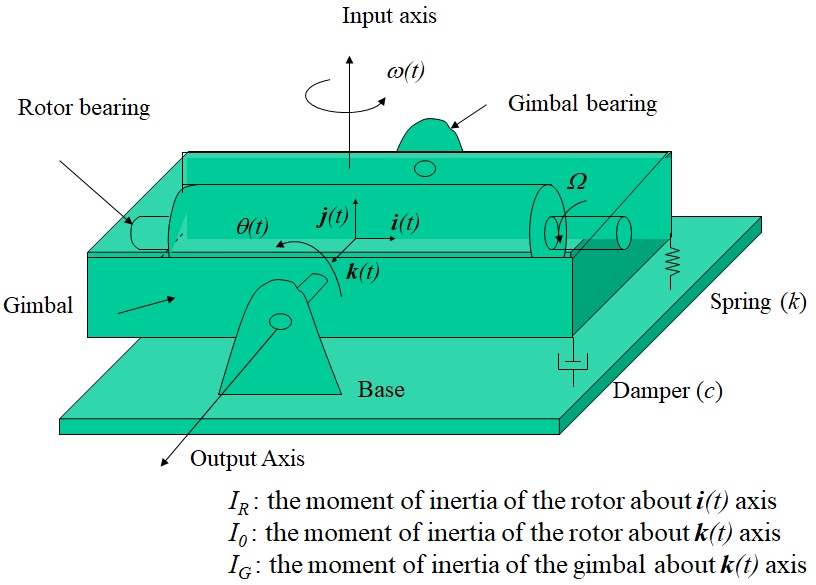
図4-1 ジャイロセンサ力学モデル
図4-1に示すように,回転するローター上に軸方向,上下方向,ジンバル支持軸方向の単位ベクトルをそれぞれ$\overrightarrow{i}(t)$,$\overrightarrow{j}(t)$,$\overrightarrow{k}(t)$とする座標系を定義する.角速度$\Omega$で回転するローター部の$\overrightarrow{i}(t)$回りの慣性モーメントを$_R$,$\overrightarrow{k}(t)$軸回りの慣性モーメントを$I_0$とする.形状から分かるように$\overrightarrow{j}(t)$軸回りの慣性モーメントは,$I_0$となる.また,ローター部を指示しているジンバル部の$\overrightarrow{k}(t)$軸回りの慣性モーメントを$I_G$とする.ジンバル右端のばねのばね定数を$k$,ダシュポットを$c$とし,ジンバル回転軸からジンバル両端までの距離を$h$とする.ローラー支持部,ジンバル右端のばね,ダシュポット部の内力を考慮したFree-body Diagramは図4-2のようになる.
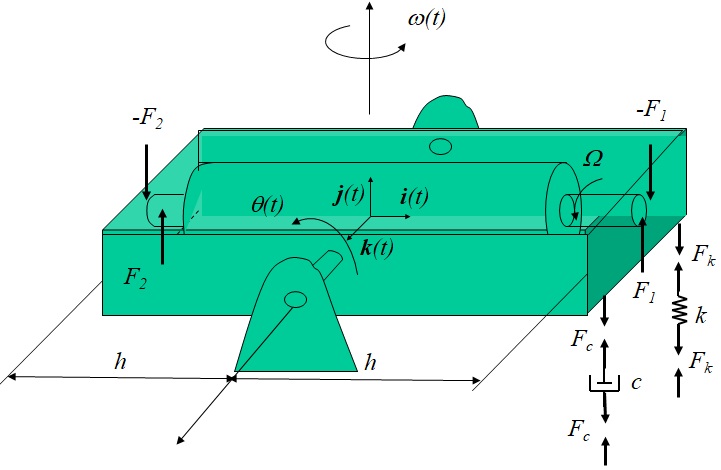
図4-2 ジャイロセンサ力学モデルFree-body Diagram
この系の回転運動に関する方程式を誘導する.この系の角運動量ベクトルは次のように表現できる.
\begin{eqnarray*}
\overrightarrow{H}\left(t\right) = I_R\Omega\overrightarrow{i}\left(t\right)+I_0\omega\left(t\right)\overrightarrow{j}\left(t\right)+I_0\frac{d\theta\left(t\right)}{dt}\overrightarrow{k}\left(t\right)
\end{eqnarray*}
回転運動を考える場合,角運動量の時間変化が作用しているモーメントの和となるということを利用する.そこで,角運動量ベクトルを時間で微分する.
\begin{eqnarray*}
\frac{d\overrightarrow{H}\left(t\right)}{dt} = I_R\Omega\frac{d\overrightarrow{i}\left(t\right)}{dt} + I_0\frac{d\omega\left(t\right)}{dt}\overrightarrow{j}\left(t\right) + I_0\omega\left(t\right)\frac{d\overrightarrow{j}\left(t\right)}{dt} + I_0\frac{d^2\theta\left(t\right)}{dt^2}\overrightarrow{k}\left(t\right) + I_0\frac{d\theta\left(t\right)}{dt}\frac{d\overrightarrow{k}\left(t\right)}{dt}
\end{eqnarray*}
ここで,
\begin{eqnarray*}
&& \frac{d\overrightarrow{i}\left(t\right)}{dt} = -\omega\left(t\right)\overrightarrow{k}\left(t\right) \\
&& \frac{d\overrightarrow{j}\left(t\right)}{dt} = -\frac{d\theta\left(t\right)}{dt}\overrightarrow{k}\left(t\right) \\
&& \frac{d\overrightarrow{k}\left(t\right)}{dt} = \omega\left(t\right)\overrightarrow{i}\left(t\right)
\end{eqnarray*}
より,次式となる.
\begin{eqnarray*}
\frac{d\overrightarrow{H}\left(t\right)}{dt} &=& -I_R\Omega\omega\left(t\right)\overrightarrow{k}\left(t\right) + I_0\frac{d\omega\left(t\right)}{dt}\overrightarrow{j}\left(t\right) - I_0\omega\left(t\right)\frac{d\theta\left(t\right)}{dt}\overrightarrow{i}\left(t\right) + I_0\frac{d^2\theta\left(t\right)}{dt^2}\overrightarrow{k}\left(t\right) + I_0\frac{d\theta\left(t\right)}{dt}\omega\left(t\right)\overrightarrow{i}\left(t\right) \\
&=& \left\{I_0\frac{d^2\theta\left(t\right)}{dt^2} -I_R\Omega\omega\left(t\right)\right\}\overrightarrow{k}\left(t\right) + I_0\frac{d\omega\left(t\right)}{dt}\overrightarrow{j}\left(t\right)
\end{eqnarray*}
よって,$\overrightarrow{k}\left(t\right)$軸回りの回転運動に対する運動方程式は次式となる.
\begin{eqnarray*}
I_0\frac{d^2\theta\left(t\right)}{dt^2} -I_R\Omega\omega\left(t\right) = h\times\left(-F_1-F_2\right)
\end{eqnarray*}
一方,ジンバルの支持軸回りの回転運動に対する運動方程式は次のようになる.
\begin{eqnarray*}
I_G\frac{d^2\theta\left(t\right)}{dt^2} = h\left(F_1 + F_2\right) - kh^2\theta\left(t\right) - ch^2\frac{d\theta\left(t\right)}{dt}
\end{eqnarray*} \begin{eqnarray*}
\left(I_0+I_G\right)\frac{d^2\theta\left(t\right)}{dt^2} + ch^2\frac{d\theta\left(t\right)}{dt} + kh^2\theta\left(t\right) =I_R\Omega\omega\left(t\right)
\end{eqnarray*}
内力によるモーメントは,作用・反作用の関係となっているので,2つの式を足すと次式を得る.
\begin{eqnarray*}
\left(I_0+I_G\right)\frac{d^2\theta\left(t\right)}{dt^2} + ch^2\frac{d\theta\left(t\right)}{dt} + kh^2\theta\left(t\right) = I_R\Omega\omega\left(t\right)
\end{eqnarray*}
即ち,センサの角速度$\omega\left(t\right)$は,次式となる.
\begin{eqnarray*}
\omega\left(t\right) = \frac{1}{I_R\Omega}\left[\left(I_0+I_G\right)\frac{d^2\theta\left(t\right)}{dt^2} + ch^2\frac{d\theta\left(t\right)}{dt} + kh^2\theta\left(t\right) \right]
\end{eqnarray*}
4.2 ジャイロセンサによる角速度計測
このセンサを使って角速度を測定した場合の出力信号について調べてみる.数値的に検討するために,図4-3に示すように前回調べた乗用車で発生している角速度を測定してみることにする.センサの諸元に関しては任意に定めることができるが,測定対象に対しては不適な設定も存在する.系としては1自由度の粘性減衰系なので,その応答特性については容易に推察されるため,値の決め方に対する考え方はある程度分かると思われる.
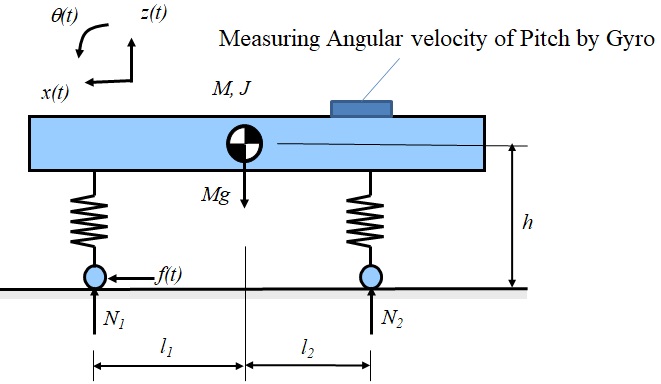
図4-3 ジャイロセンサに関する数値実験
ここでは,適当に通知を与えて調べてみる.数値実験プログラムは例えば図4-4のようになる.

図4-4 プログラム例
4.4 演習
実際にプログラムを作成し,結果について考察せよ.




