6.Bang Bang制御例
6.1 動的な過程の最適制御
制御理論に則り,$\mathbf{u}$を$m$次元の制御ベクトル,$\mathbf{x}$を$n$次元の状態ベクトルとする.制御ベクトル$\mathbf{u}$によって制御される対象システム$S$の応答は,状態方程式
\begin{eqnarray*}
\frac{d\mathbf{x}}{dt} = \mathbf{f}\left(\mathbf{x},\mathbf{u},t\right)
\end{eqnarray*}
と,出力方程式
\begin{eqnarray*}
\mathbf{y} = \mathbf{g}\left(\mathbf{x},\mathbf{u},t\right)
\end{eqnarray*}
によって表わされる.$\mathbf{y}$は$p$次元出力ベクトルである.また,ここでは$\mathbf{f}$,$\mathbf{g}$として一般的な非線形関数を考えている.実際のシステムとの対応から,制御ベクトルおよび状態ベクトルの要素はその値域が限られるから,システムを制御するときには
\begin{eqnarray*}
&& \mathbf{x}\in X \\
&& \mathbf{u}\in U
\end{eqnarray*}
のような領域を満たすように実現する必要がある.よって,$\mathbf{y}$は対象システムの安全な運転範囲やサーボ機構の固定された軌道などに対応し,状態制約と呼ばれる.$\mathbf{u}$の制約条件は,入力操作器の可動範囲や増幅器の線形動作範囲に対応し,許容制御(admissible control)と呼ばれる.
6.2 最短時間制御
現実的な問題として制御入力が
\begin{eqnarray*}
\left|u\right| \leq U_0
\end{eqnarray*}
のように,最大(飽和)入力が存在する場合を考える.最大入力を仮定した場合には,上述の”条件付き最適化”問題となり,”最短時間制御”を考えることができる.この場合の入力は,一般にBang-Bang入力と呼ばれ図6-1のようになる.即ち,最大入力を加え(例えば,機械システムを駆動し),$t=t_1$を切替時刻として,今度は向き(符号)が逆側の最大入力を加え(ブレーキをかけ),目標位置に到達する時刻$t=t_2$で入力を零にして停止させる,ような制御方法である.
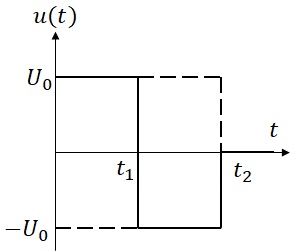
図6-1 Bang-Bang入力
質量$m$の1自由度質点系について,入力を$f(t)$として,切り替え時間,停止時間を定めてみる.変位を$x(t)$とすると,運動方程式は
\begin{eqnarray*}
m\ddot{x}(t)=f(t)
\end{eqnarray*}
停止状態からの駆動として,初期条件を$t=0$で,$x(0)=0$,$\dot{x}(0)=0$として,Laplace変換すると
\begin{eqnarray*}
ms^2X(s)=F(s)
\end{eqnarray*}
よって,
\begin{eqnarray*}
X(s)=\frac{1}{ms^2}F(s)
\end{eqnarray*}
畳み込み積分を用いて逆変換すると次式を得る.
\begin{eqnarray*}
x(t)=\int_0^t\frac{1}{m}\left(t-\tau\right)f(\tau)d\tau
\end{eqnarray*}
図6-1に示す入力を想定して$f(t)$を考えると,
\begin{eqnarray*}
x(t)=\int_0^t\frac{1}{m}\left(t-\tau\right)U_0d\tau + \int_{t_1}^t\frac{1}{m}\left(t-\tau\right)\left(-2U_0\right)d\tau + \int_{t_2}^t\frac{1}{m}\left(t-\tau\right)U_0d\tau
\end{eqnarray*}
であり,$0\leq t\leq t_1$では第一項のみとなり,切り替え時間を過ぎると第二項を加え,停止時間以降の挙動がすべての項を計算した結果となり,次のようになる.
\begin{eqnarray*}
x(t)=\frac{U_0}{m}\left\{\frac{1}{2}t^2-\left(t-t_1\right)^2 + \frac{1}{2}\left(t-t_2\right)^2\right\}
\end{eqnarray*}
また,各時刻毎の速度は次のようになる.
\begin{eqnarray*}
\frac{dx(t)}{dt}= \frac{U_0}{m}\left\{\begin{array}{ll}
t & 0\leq t \leq t_1 \\
-t+2t_1 & t_1\leq t\leq t_2 \\
2t_1-t_2 & t_2\leq t
\end{array}\right.
\end{eqnarray*}
終点において静止するためには,速度が零となることが必要なので,
\begin{eqnarray*}
&& 2t_1 - t_2 =0 \\
&& \therefore t_2 = 2t_1
\end{eqnarray*}
また,$t=t_2$において,目標位置$x_T$に移動させるとすると,
\begin{eqnarray*}
x(t_2)=\frac{U_0}{m}\left\{\frac{1}{2}\left(t_2\right)^2-\left(t_2-t_1\right)^2 + \frac{1}{2}\left(t_2-t_2\right)^2\right\} = x_T
\end{eqnarray*}
よって,$t_2=t_1$を代入して
\begin{eqnarray*}
\frac{U_0}{m}\left(2t_1^2-t_1^2\right) = x_T
\end{eqnarray*}
即ち,切り替え時間および停止時間は次のようになる.
\begin{eqnarray*}
&& t_1 = \sqrt{\frac{mx_T}{U_0}} \\
&& t_2 = 2t_1= 2\sqrt{\frac{mx_T}{U_0}}
\end{eqnarray*}
6.3 演習
実際にプログラムを作成し,最短時間制御について考察せよ.

