7.並進運動と回転運動が同時に起こる系のモデル
7.1 天井クレーンモデル
機械システムの動的な動作において,単なる移動(並進運動),支点回りの回転運動など動的応答を単体として取り合うことが難しい現象も数多く存在する.ここでは,天井クレーンのモデルの一つである,水平方向に移動可能な移動台車に懸架された剛体振り子系に対する運動方程式を導出し,システムの動的挙動について調べてみる.
対象とする移動台車-振り子系モデルを図7-1に示す.
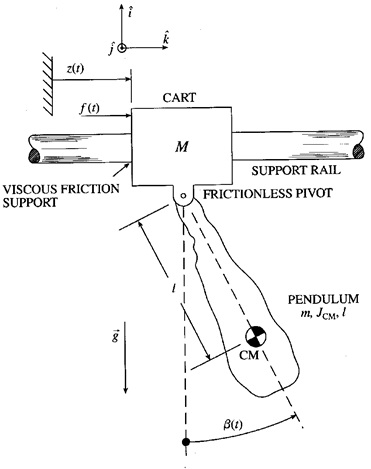
図7-1 移動台車‐振り子系モデル
モデル化に際して,図7-2に示す項目を仮定する.ここで,パラメータとして定められていない移動台車と走行レール間の粘性減衰係数は,$D$とする.

図7-2 モデル化における条件設定
7.2 運動方程式の導出
図7-1に示すように水平方向変位$z(t)$の単位ベクトルを$\mathbf{k}$,鉛直上向きの単位ベクトルを$\mathbf{i}$とあり,これらの単位ベクトルと”右手系”を組むように紙面上向きを正とする単位ベクトル$\mathbf{j}$を取る.移動台車(重心)ベクトル$\mathbf{r}_c$は,
\begin{eqnarray*}
\mathbf{r}_c = z(t)\mathbf{k}
\end{eqnarray*}
と表現できるので,速度ベクトル$\mathbf{v}_c$は次のようになる.
\begin{eqnarray*}
\mathbf{v}_c = \dot{z}(t)\mathbf{k}
\end{eqnarray*}
また,これに連結されている振り子重心位置ベクトルは
\begin{eqnarray*}
\mathbf{r}_G = z(t)\mathbf{k} + l\sin\beta(t)\mathbf{k} - l\cos\beta(t)\mathbf{i}
\end{eqnarray*}
となるので,速度ベクトルは次式となる.
\begin{eqnarray*}
\mathbf{v}_G = \dot{z}(t)\mathbf{k} + l\dot{\beta}(t)\cos\beta(t)\mathbf{k} + l\dot{\beta}(t)\sin\beta(t)\mathbf{i}
= \left\{\dot{z}(t) + l\dot{\beta}(t)\cos\beta(t)\right\}\mathbf{k} + l\dot{\beta}(t)\sin\beta(t)\mathbf{i}
\end{eqnarray*}
一方,この系に対するFree-body Diagramを考えると図7-3のようになる.
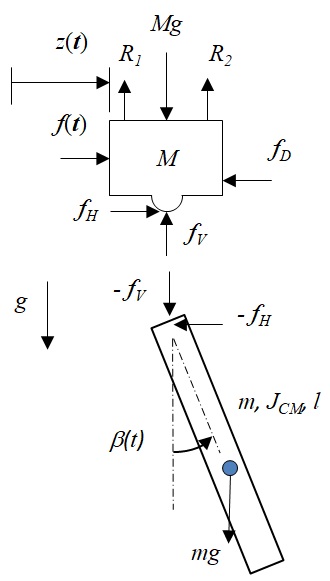
図7-3 移動台車‐振り子系
図7-3において仮定した各力をベクトルで表わす.移動台車は大きさを持っているように描いているが,実際には作用力は重心に作用することを仮定しておりその力ベクトル$\mathbf{f}_c$は
\begin{eqnarray*}
\mathbf{f}_c = \left\{f(t) + F_H - F_D\right\}\mathbf{k} + \left(R_1+R_2+F_V-Mg\right)\mathbf{i}
\end{eqnarray*}
振り子の作用する力は,作用点が二か所あり,連結位置において
\begin{eqnarray*}
\mathbf{f}_p = -F_H\mathbf{k} -F_V\mathbf{i}
\end{eqnarray*}
重心位置に
\begin{eqnarray*}
\mathbf{f}_G = -mg\mathbf{i}
\end{eqnarray*}
となる.重心位置に対する連結位置の相対位置ベクトル$\mathbf{r}_{Gp}$は
\begin{eqnarray*}
\mathbf{r}_{Gp} = \mathbf{r}_c- \mathbf{r}_G = -l\sin\beta(t)\mathbf{k} + l\cos\beta(t)\mathbf{i}
\end{eqnarray*}
となるので,振り子の重心回りに作用しているモーメント$\mathbf{M}_G$は次式となる.
\begin{eqnarray*}
\mathbf{M}_G &=& \mathbf{r}_c\times\mathbf{f}_p = \left\{-l\sin\beta(t)\mathbf{k} + l\cos\beta(t)\mathbf{i}\right\}\times\left\{-F_H\mathbf{k} -F_V\mathbf{i}\right\} \\
&=& F_Hl\cos\beta(t)+F_Vl\sin\beta(t)\mathbf{j}
\end{eqnarray*}
各運動に対して,Newtonの第2法則を適用する.移動台車については,
\begin{eqnarray*}
&& \frac{d}{dt}\left(M\mathbf{v}_c\right) = \mathbf{f}_c \\ \\
&& \therefore M\ddot{z}(t)\mathbf{k} = \left\{f(t) + F_H - F_D\right\}\mathbf{k} + \left(R_1+R_2+F_V-Mg\right)\mathbf{i}
\end{eqnarray*}
台車の移動を考えるので,次の運動方程式が定まる.
\begin{eqnarray*}
M\ddot{z}(t) = f(t) + F_H - F_D
\end{eqnarray*}
剛体振子の並進運動に関しては,
\begin{eqnarray*}
\frac{d}{dt}\left(m\mathbf{v}_p\right) = \mathbf{f}_p + \mathbf{f}_G
\end{eqnarray*}
よって
\begin{eqnarray*}
m\left[\left\{\ddot{z}(t) + l\ddot{\beta}(t)\cos\beta(t)-l\dot{\beta}(t)^2\sin\beta(t) \right\}\mathbf{k} + \left\{l\ddot{\beta}(t)\sin\beta(t)+l\dot{\beta}(t)^2\cos\beta(t)\right\}\mathbf{i}\right] = -F_H\mathbf{k} -F_V\mathbf{i}-mg\mathbf{i}
\end{eqnarray*}
よって,$F_H$,$F_V$は次式となる.
\begin{eqnarray*}
&& F_H = -m\left\{\ddot{z}(t) + l\ddot{\beta}(t)\cos\beta(t)-l\dot{\beta}(t)^2\sin\beta(t) \right\} \\
&& F_V = -mg -m\left\{l\ddot{\beta}(t)\sin\beta(t)+l\dot{\beta}(t)^2\cos\beta(t)\right\}
\end{eqnarray*}
また,$F_D$は
\begin{eqnarray*}
F_D = -D\dot{z}(t)
\end{eqnarray*}
となるので,$F_H$,$F_D$を移動台車の運動方程式に代入すると
\begin{eqnarray*}
M\ddot{z}(t) = f(t) -m\left\{\ddot{z}(t) + l\ddot{\beta}(t)\cos\beta(t)-l\dot{\beta}(t)^2\sin\beta(t) \right\} - D\dot{z}(t)
\end{eqnarray*}
また,振り子の重心回りの回転運動に関して次式が成り立つ.
\begin{eqnarray*}
\frac{d}{dt}\left(J_{CM}\dot{\beta}(t)\right)\mathbf{j} = \mathbf{M}_G = F_Hl\cos\beta(t)+F_Vl\sin\beta(t)\mathbf{j}
\end{eqnarray*}
$F_H$,$F_V$を代入すると次式となる.
\begin{eqnarray*}
J_{CM}\ddot{\beta}(t) = -m\left\{\ddot{z}(t) + l\ddot{\beta}(t)\cos\beta(t)-l\dot{\beta}(t)^2\sin\beta(t) \right\}l\cos\beta(t)-\left[mg+m\left\{l\ddot{\beta}(t)\sin\beta(t)+l\dot{\beta}(t)^2\cos\beta(t)\right\} \right]l\sin\beta(t)
\end{eqnarray*}
従って,この系の運動方程式は次のようになる.
\begin{eqnarray*}
&& \left(M+m\right)\ddot{z}(t) + D\dot{z}(t)+ ml\left\{\ddot{\beta}(t)\cos\beta(t)-\dot{\beta}(t)^2\sin\beta(t) \right\} = f(t) \\
&& \left(J_{CM}+ml^2\right)\ddot{\beta}(t) + m\ddot{z}(t)l\cos\beta(t) + mgl\sin\beta(t)=0
\end{eqnarray*}
この系は,入力$f(t)$によって駆動されるので,この力により様々な挙動を示すことになる.
7.3 演習
一定距離駆動する数値実験を行い,動かし方に応じて発生する系の挙動について考察せよ.



