8.航空機の力学
8.1 航空機飛行モデル
図8-1に示すように,航空機が紙面に示す面内を飛行する場合を考える.ここでは,面内に規定される空間上を”推力”と”昇降陀”を用いて,機体の上昇,下降を行いながら飛行する場合を想定する.
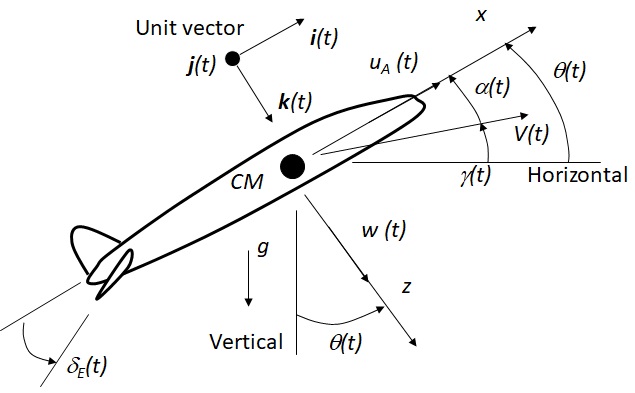
図8-1 航空機飛行モデル
モデル化に際して,図8-2に示す項目を仮定し,$x$方向の飛行速度を$u_A(t)$,$z$方向の飛行速度を$w(t)$,鉛直下向きを基準とする飛行姿勢角度を$\theta(t)$とする.また,航空機の質量は$m$とし,重心を通る紙面に水力な軸回りの慣性モーメントを$I_{yy}$とおく.

図8-2 モデル化における条件設定
8.2 運動方程式の導出
航空機重心位置の速度ベクトルは次式となる.
\begin{eqnarray*}
\mathbf{V}(t) = u_A(t)\mathbf{i}(t) + w(t)\mathbf{k}(t)
\end{eqnarray*}
機体に作用する力は,推力,揚力,抗力など様々な流体力が作用し,それらは,翼形状,飛行速度など様々なパラメータにより変化することが知られている.そこで,それらの推力と空気力学的な作用力の合力を飛行状態を示すパラメータを独立変数とする関数として仮定し,次式のように置く.
\begin{eqnarray*}
\mathbf{F}(t) = X\left(u_A, w,, \delta_E, \delta_T\right)\mathbf{i}(t) + Z\left(u_A, w, \dot{\theta},\delta_E, \delta_T\right)\mathbf{k}(t)
\end{eqnarray*}
下向きに作用する重力ベクトルを式で示すと次式となる.
\begin{eqnarray*}
\mathbf{G}(t) = -mg\sin\theta(t)\mathbf{i}(t) + mg\cos\theta(t)\mathbf{k}(t)
\end{eqnarray*}
また,重心回りに作用する空気力学的作用モーメントの合計を次のように仮定する.
\begin{eqnarray*}
\mathbf{M}(t) = M\left(u_A, w, \dot{w}, \dot{\theta},\delta_E, \delta_T\right)\mathbf{j}(t)
\end{eqnarray*}
よって,Newtonの第2法則から,次のような運動方程式を得る.
\begin{eqnarray*}
&& \frac{d}{dt}\left\{m\mathbf{V}(t)\right\} = \mathbf{F}(t) + \mathbf{G}(t) \\
&& \frac{d}{dt}\left\{I_{yy}\dot{\theta}(t)\right\} =\mathbf{M}(t)
\end{eqnarray*}
ここで,
\begin{eqnarray*}
\frac{d}{dt}\left\{\mathbf{V}(t)\right\} = \left\{\dot{u}_A(t)+\dot{\theta}(t)w(t)\right\}\mathbf{i}(t) + \left\{\dot{w}(t)-\dot{\theta}(t)u_A(t)\right\}\mathbf{k}(t)
\end{eqnarray*}
より,各成分ごとに運動方程式を示すと次式の様になる.
\begin{eqnarray*}
&& m\left\{\dot{u}_A(t)+\dot{\theta}(t)w(t)\right\} = X\left(u_A, w,, \delta_E, \delta_T\right)-mg\sin\theta(t) \\
&& m\left\{\dot{w}(t)-\dot{\theta}(t)u_A(t)\right\} = Z\left(u_A, w, \dot{\theta},\delta_E, \delta_T\right) + mg\cos\theta(t) \\
&& I_{yy}\ddot{\theta} = M\left(u_A, w, \dot{w}, \dot{\theta},\delta_E, \delta_T\right)
\end{eqnarray*}
空気力学的な作用力は,関数形で示したように飛行状態に応じて変化する.そこで,運動方程式をある”平衡状態”からのずれを記述するものに近似して,ある飛行状態からの状態変化を表わす運動方程式に変換する.即ち,ある安定して飛行している状態(平衡状態)の各値を$\left(u_{A0}, w_0, \theta_0, \delta_{E0}, \delta_{T0}\right)$とし,その状態からの微小な変化を次のように考える.
\begin{eqnarray*}
&& u(t)=u_{A0}+\Delta u_A(t),\quad \dot{u}_A= = \Delta\dot{u}_A(t) \\
&& w(t)=w_0+\Delta w(t),\quad \dot{w}(t)=\Delta\dot{w}(t) \\
&& \theta(t)=\theta_0+\Delta\theta(t),\quad \dot{\theta}(t)=\Delta\dot{\theta}(t)\\
&& \delta_E(t)=\delta_{E0}+\Delta\delta_E(t) \\
&& \delta_T(t)=\delta_{T0}+\Delta\delta_T(t)
\end{eqnarray*}
この変化に対して,書く作用力,作用モーメントも同様に,平衡状態での値$\left(X_0,Z_0,M_0\right)$からの微小変化を次のように考える.
\begin{eqnarray*}
&& X\left(u_A, w,, \delta_E, \delta_T\right) =X_0+\Delta X\left(u_A, w,, \delta_E, \delta_T\right)\\
&& Z\left(u_A, w, \dot{\theta},\delta_E, \delta_T\right)=Z_0+\Delta Z\left(u_A, w, \dot{\theta},\delta_E, \delta_T\right) \\
&& M\left(u_A, w, \dot{w}, \dot{\theta},\delta_E, \delta_T\right)=M_0+\Delta M\left(u_A, w, \dot{w}, \dot{\theta},\delta_E, \delta_T\right)
\end{eqnarray*}
これらの関係を運動方程式に代入する.
\begin{eqnarray*}
&& m\left[\Delta\dot{u}_A(t)+\Delta\dot{\theta}(t)\left\{w_0+\Delta w(t)\right\}\right] = X_0+\Delta X\left(u_A, w,, \delta_E, \delta_T\right)-mg\sin\left\{\theta_0+\Delta\theta(t)\right\} \\
&& m\left[\Delta\dot{w}(t)-\Delta\dot{\theta}(t)\left\{u_{A0}+\Delta u_A(t)\right\}\right] = Z_0+\Delta Z\left(u_A, w, \dot{\theta},\delta_E, \delta_T\right) + mg\cos\left\{\theta_0+\Delta\theta(t)\right\} \\
&& I_{yy}\Delta\ddot{\theta} = M_0+\Delta M\left(u_A, w, \dot{w}, \dot{\theta},\delta_E, \delta_T\right)
\end{eqnarray*}
変形すると
\begin{eqnarray*}
&& m\left[\Delta\dot{u}_A(t)+w_0\Delta\dot{\theta}(t)+\Delta\dot{\theta}(t)\Delta w(t)\right] = X_0+\Delta X\left(u_A, w,, \delta_E, \delta_T\right) - mg\sin\theta_0\cos\left\{\Delta\theta(t)\right\} - mg\cos\theta_0\sin\left\{\Delta\theta(t)\right\} \\
&& m\left[\Delta\dot{w}(t)-u_{A0}\Delta\dot{\theta}(t) -\Delta\dot{\theta}(t)\Delta u_A(t)\right] = Z_0+\Delta Z\left(u_A, w, \dot{\theta},\delta_E, \delta_T\right) + mg\cos\theta_0\cos\left\{\Delta\theta(t)\right\} - mg\sin\theta_0\sin\left\{\Delta\theta(t)\right\} \\
&& I_{yy}\Delta\ddot{\theta} = M_0+\Delta M\left(u_A, w, \dot{w}, \dot{\theta},\delta_E, \delta_T\right)
\end{eqnarray*}
平衡状態では,$\Delta$の部分が全て零となるので,次の関係が成り立つ.
\begin{eqnarray*}
&& X_0 - mg\sin\theta_0\cos\left\{0\right\} = 0 \\
&& Z_0 + mg\cos\theta_0\cos\left\{0\right\} = 0 \\
&& M_0 =0
\end{eqnarray*}
即ち,並進運動に関しては,重力と釣り合っており,面内の回転も発生しない状態で飛行している状態が平衡状態となる.更に,$\Delta$の変化を微小とすると$\Delta^2$の項は無視できるので,運動方程式は次式となる.
\begin{eqnarray*}
&& \Delta\dot{u}_A(t)+w_0\Delta\dot{\theta}(t) + g\cos\theta_0\sin\left\{\Delta\theta(t)\right\} = \frac{1}{m}\Delta X\left(u_A, w,, \delta_E, \delta_T\right) \\
&& \Delta\dot{w}(t)-u_{A0}\Delta\dot{\theta}(t) + g\sin\theta_0\sin\left\{\Delta\theta(t)\right\} = \frac{1}{m}\Delta Z\left(u_A, w, \dot{\theta},\delta_E, \delta_T\right) \\
&& \Delta\ddot{\theta} = \frac{1}{I_{yy}}\Delta M\left(u_A, w, \dot{w}, \dot{\theta},\delta_E, \delta_T\right)
\end{eqnarray*}
ここで,各変化量の平衡状態$0$からの微小変化に対して,対応する力とモーメントのTalor展開を考える.即ち,複数の独立変数に対するTalor展開を1次のみ考えると次のようになる.
\begin{eqnarray*}
&& \Delta X\left(u_A, w,, \delta_E, \delta_T\right) \fallingdotseq \left[\frac{\partial X}{\partial u_A}\right]_0\Delta u_A(t) + \left[\frac{\partial X}{\partial w}\right]_0\Delta w(t) + \left[\frac{\partial X}{\partial\delta_E}\right]_0\Delta\delta_E(t) +\left[\frac{\partial X}{\delta_T}\right]_0\Delta\delta_T(t) \\
&& \Delta Z\left(u_A, w, \dot{\theta},\delta_E, \delta_T\right) \fallingdotseq \left[\frac{\partial Z}{\partial u_A}\right]_0\Delta u_A(t) + \left[\frac{\partial Z}{\partial w}\right]_0\Delta w(t)+ \left[\frac{\partial Z}{\partial\dot{\theta}}\right]_0\Delta\dot{\theta}(t) + \left[\frac{\partial Z}{\partial\delta_E}\right]_0\Delta\delta_E(t) +\left[\frac{\partial Z}{\delta_T}\right]_0\Delta\delta_T(t) \\
&& \Delta M\left(u_A, w, \dot{w}, \dot{\theta},\delta_E, \delta_T\right)\fallingdotseq \left[\frac{\partial M}{\partial u_A}\right]_0\Delta u_A(t) + \left[\frac{\partial M}{\partial w}\right]_0\Delta w(t) + \left[\frac{\partial M}{\partial\dot{w}}\right]_0\Delta\dot{w}(t)+ \left[\frac{\partial M}{\partial\dot{\theta}}\right]_0\Delta\dot{\theta}(t) + \left[\frac{\partial M}{\partial\delta_E}\right]_0\Delta\delta_E(t) +\left[\frac{\partial M}{\delta_T}\right]_0\Delta\delta_T(t)
\end{eqnarray*}
よって,この場合の運動方程式は次のようになる.
\begin{eqnarray*}
&& \Delta\dot{u}_A(t)+w_0\Delta\dot{\theta}(t) + g\cos\theta_0\sin\left\{\Delta\theta(t)\right\} = \frac{1}{m}\left\{\left[\frac{\partial X}{\partial u_A}\right]_0\Delta u_A(t) + \left[\frac{\partial X}{\partial w}\right]_0\Delta w(t) + \left[\frac{\partial X}{\partial\delta_E}\right]_0\Delta\delta_E(t) +\left[\frac{\partial X}{\delta_T}\right]_0\Delta\delta_T(t)\right\}
\\
&& \Delta\dot{w}(t)-u_{A0}\Delta\dot{\theta}(t) + g\sin\theta_0\sin\left\{\Delta\theta(t)\right\} = \frac{1}{m}\left\{\left[\frac{\partial Z}{\partial u_A}\right]_0\Delta u_A(t) + \left[\frac{\partial Z}{\partial w}\right]_0\Delta w(t)+ \left[\frac{\partial Z}{\partial\dot{\theta}}\right]_0\Delta\dot{\theta}(t) + \left[\frac{\partial Z}{\partial\delta_E}\right]_0\Delta\delta_E(t) +\left[\frac{\partial Z}{\delta_T}\right]_0\Delta\delta_T(t)\right\} \\
&& \Delta\ddot{\theta} = \frac{1}{I_{yy}}\left\{\left[\frac{\partial M}{\partial u_A}\right]_0\Delta u_A(t) + \left[\frac{\partial M}{\partial w}\right]_0\Delta w(t) + \left[\frac{\partial M}{\partial\dot{w}}\right]_0\Delta\dot{w}(t)+ \left[\frac{\partial M}{\partial\dot{\theta}}\right]_0\Delta\dot{\theta}(t) + \left[\frac{\partial M}{\partial\delta_E}\right]_0\Delta\delta_E(t) +\left[\frac{\partial M}{\delta_T}\right]_0\Delta\delta_T(t)\right\}
\end{eqnarray*}
8.3 演習
一定飛行速度で飛行する場合の数値実験を行い,系の挙動について考察せよ.


