
2016年度 数楽工作倶楽部 番外編
立方八面体の双対多面体
2016年4月29日に、防府市青少年科学館ソラールで行われている企画展「数と形のふしぎなあそび ラ・ビレット展」に連動した特別講座「うつくしい立体をつくろう」に、工作倶楽部の学生とともに出講してきました。小学3年生から一般と幅広い方々を対象とするため、数式を使った数学の話は避け、工作を通じてタイトルの「うつくしい立体」を「数学的」に感じられる講義内容としました。(講座のスライド 2.1MB)
この講座で製作したのは、以前の工作倶楽部でも製作した「菱形十二面体」と、その双対多面体である「立方八面体」です。
以前に製作した菱形十二面体はギザギザの4本の帯を編んで作りましたが、今回は時間と対象年齢を考慮し、どちらの立体も展開図から製作しました。
菱形十二面体の製作
菱形十二面体の型紙(2枚使用します)
紙工作で通常の展開図から多面体を作るとき、最も困難なのは最後ののりづけです。のりしろが立体の内部にあり、接着するときに物理的にその部分を押さえることが困難なため、どうしても形が崩れてしまいます。(ギザギザの帯を編んで作る場合にはその困難がありません。)
そこで、今回は多少無駄な部分があるのを承知で、多面体としては未完成の2個の部品を作り、それらを組み合わせて完成させる手法を使いました。
立方八面体の製作
立方八面体の型紙(2枚使用します)
立方八面体も、菱形十二面体と同様に、2個の部品を組み合わせて完成させます。
互いの部品の正方形の「みみ」の部分を差し込んでゆくと、結構しかりとしたものが出来上がります。
講座では、製作した二つの立体: 「菱形十二面体」と「立方八面体」が双対多面体となることを、「頂点と面の数の対応」という観点からのみ紹介しましたが、実際の模型を手にすると、その事実をより実感することができます。
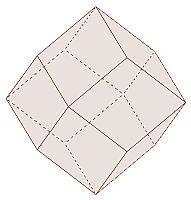 ⇒
⇒ 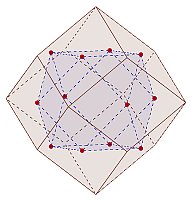 ⇒
⇒ 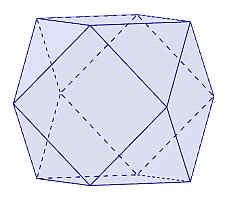
(「菱形十二面体」の各面の中心を頂点とする立体が「立方八面体」となる)

(透明のプラ板で作った菱形十二面体の面の中心同士を針金で結んだモデル)
それでは、立方八面体の面の中心同士を結ぶと、菱形十二面体になるでしょうか?
残念ながら、そのようにはなりません。
実際、双対多面体の関係とは、「面」と「頂点」を入れ替えた関係というだけで、必ずしも面の中心同士を結んで現れる立体というわけではありません。
ちなみに、ここで立方八面体の内部に現れる立体は、正八面体の各面の上に、直角二等辺三角形を側面に持つ三角錐をくっつけた、24枚の直角二等辺千角形の面を持つ多面体です。この立体は、12枚のユニット折り紙で作られる立体と同じです。